Computer Vision and Edge Detection

• Computer Vision
  • Introduction to Computer Vision
  • Fundamental Concepts
  • Mathematical Formulation
• Edge Detection
  • Why Use Convolution for Edge Detection?
    • What Does a Filter Do?
  • Mathematical Example
    • Step-by-Step Convolution (No Padding, Stride = 1)
    • Second Convolution Step (Next to Right)
    • Full Output Matrix (4x4)
  • Key Insight:
  • Edge Detection Techniques
    • 1. Sobel Operator
    • 2. Prewitt Operator
    • 3. Laplacian of Gaussian (LoG)
    • 4. Canny Edge Detection
    • 5. Difference of Gaussians (DoG)

Computer Vision

Introduction to Computer Vision

Computer Vision is a field of artificial intelligence (AI) that enables machines to interpret and understand visual information from the world. It encompasses tasks such as image recognition, object detection, and segmentation.

Real-World Applications

• Facial Recognition: Used in security systems and social media tagging.
• Medical Imaging: Helps in detecting diseases using X-rays, MRIs, and CT scans.
• Autonomous Vehicles: Enables self-driving cars to recognize objects and road signs.
• Industrial Automation: Used for defect detection in manufacturing.

Fundamental Concepts

• Pixels: The smallest unit in an image.
• Grayscale and Color Images: Difference between single-channel and multi-channel images.
• Resolution: Number of pixels in an image.
• Image Representation: Images as matrices of pixel values.

Mathematical Formulation

An image can be represented as a matrix:

$$I(x,y)\in {\mathbb{R}}^{m\times n\times c}$$

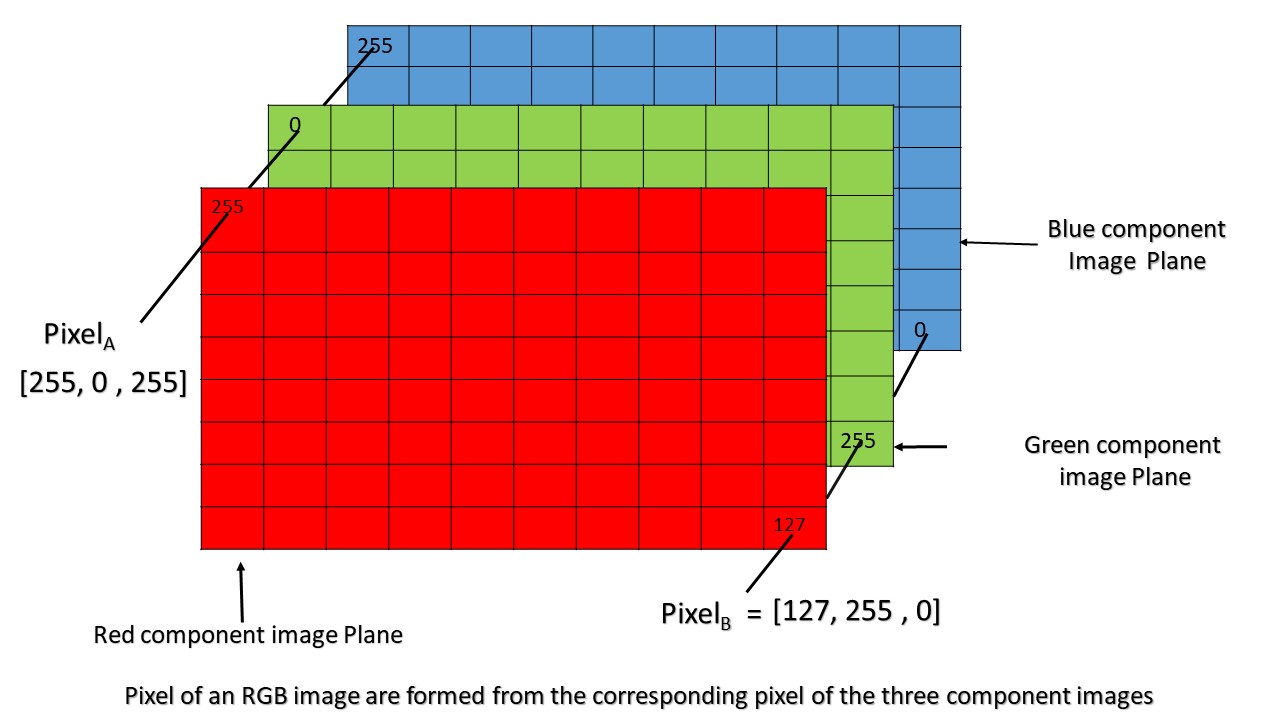
where $m$ and $n$ represent height and width, and $c$ represents the number of color channels (1 for grayscale, 3 for RGB images).

Edge Detection

Why Use Convolution for Edge Detection?

Edge detection aims to find points in an image where the intensity changes sharply. These points often correspond to boundaries of objects, texture changes, or discontinuities in depth. To detect these changes, we apply convolution operations with specific filters.

Convolution is a mathematical operation that helps us apply a small matrix (called a filter or kernel) across the entire image to detect specific patterns like edges.

What Does a Filter Do?

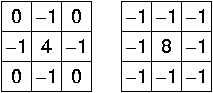
A filter is essentially a small grid of numbers (e.g., $3x3$) that slides across the image and emphasizes certain features:

• Edge filters highlight intensity changes
• Blur filters smooth the image
• Sharpening filters enhance details

In edge detection, filters are designed to detect high spatial frequency changes—essentially, edges.

Mathematical Example

$$I=\left[\begin{array}{cccccc}12& 15& 14& 10& 9& 10\\ 18& 20& 22& 17& 14& 12\\ 24& 28& 30& 26& 20& 18\\ 30& 33& 35& 32& 28& 25\\ 22& 25& 28& 24& 22& 20\\ 15& 17& 19& 18& 16& 15\end{array}\right]$$

We apply a vertical Sobel filter $K_v$:

$$K_v=\left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right]$$

This filter detects vertical edges by highlighting horizontal intensity transitions.

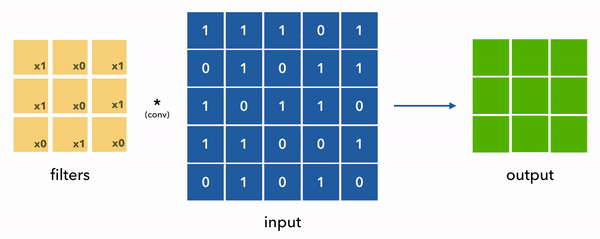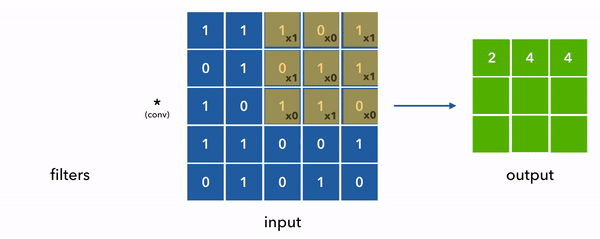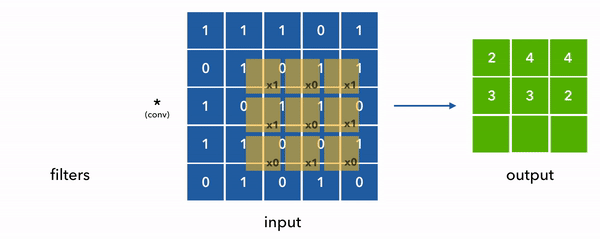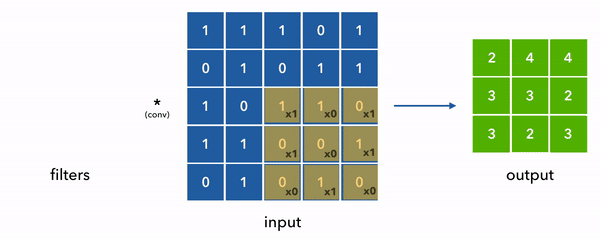
Step-by-Step Convolution (No Padding, Stride = 1)

Let’s compute the top-left value of the output matrix. We place the filter on the top-left 3x3 window of ( I ):

Window:

$$\left[\begin{array}{ccc}12& 15& 14\\ 18& 20& 22\\ 24& 28& 30\end{array}\right]$$

Element-wise multiplication and sum:

$$(-1\cdot 12)+(0\cdot 15)+(1\cdot 14)+(-2\cdot 18)+(0\cdot 20)+(2\cdot 22)+(-1\cdot 24)+(0\cdot 28)+(1\cdot 30)$$

$$=-12+0+14-36+0+44-24+0+30=16$$

So, the top-left value of the output matrix is 16.

Second Convolution Step (Next to Right)

New window (move filter one step to the right):

$$\left[\begin{array}{ccc}15& 14& 10\\ 20& 22& 17\\ 28& 30& 26\end{array}\right]$$

Apply the same operation:

$$(-1\cdot 15)+(0\cdot 14)+(1\cdot 10)+(-2\cdot 20)+(0\cdot 22)+(2\cdot 17)+(-1\cdot 28)+(0\cdot 30)+(1\cdot 26)$$

$$=-15+0+10-40+0+34-28+0+26=-13$$

So, second value is -13.

Full Output Matrix (4x4)

After sliding the filter across the 6x6 image, we get the 4x4 output:

$$I\ast K_v=\left[\begin{array}{cccc}16& -13& -25& -26\\ 20& -11& -22& -24\\ 12& -8& -18& -16\\ 4& -5& -9& -8\end{array}\right]$$

This matrix highlights the vertical edges in the original image—areas where pixel intensities change most dramatically from left to right.

The result of convolving the image with these filters gives us areas of strong gradient—edges.

Key Insight:

Filters translate the idea of change in pixel values into a computable quantity.

Edge Detection Techniques

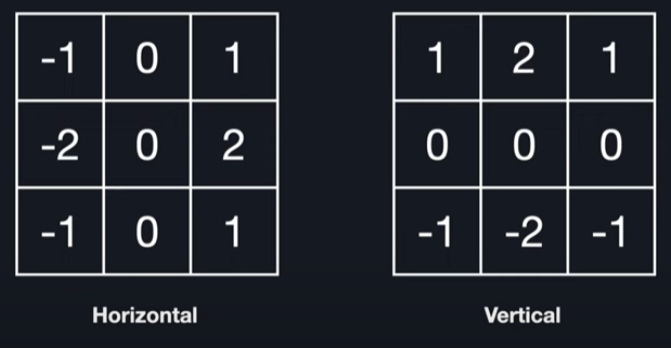
1. Sobel Operator

• Combines Gaussian smoothing and differentiation.
• Horizontal ($G_x$) and vertical ($G_y$) gradients are calculated using predefined 3x3 kernels. $$3x3\text{(}SobelKernels)$$
  
• The gradient magnitude is: $$G=\sqrt{G_x^2+G_y^2},\theta ={\tan }^{-1}\left(\frac{G_y}{G_x}\right)$$
• Commonly used due to simplicity and noise resistance.
• Watch this youtube video

2. Prewitt Operator

• Similar to Sobel, but with uniform weights. $$3x3\text{(}PrewittKernels)$$
  
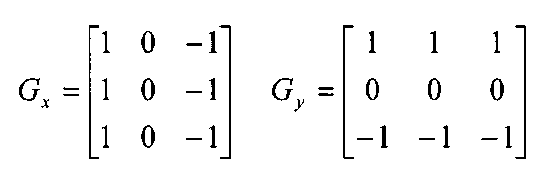
• Slightly less sensitive to noise compared to Sobel.

3. Laplacian of Gaussian (LoG)

• A second derivative method.
• Detects edges by identifying zero-crossings after applying the Laplacian to a Gaussian-smoothed image.
  
• Equation: $${\nabla }^{2}I=\frac{{\partial }^{2}I}{\partial x^2}+\frac{{\partial }^{2}I}{\partial y^2}$$
• Sensitive to noise, hence Gaussian smoothing is applied first.

4. Canny Edge Detection

A multi-stage algorithm designed for optimal edge detection:

1. Gaussian Filtering: Noise reduction.
2. Gradient Calculation: Using Sobel filters.
3. Non-Maximum Suppression: Thinning the edges.
4. Double Thresholding: Classify edges as strong, weak, or non-edges.
5. Hysteresis: Connect weak edges to strong ones if they are adjacent.

Canny is widely used in practice for its high accuracy and low false detection.

5. Difference of Gaussians (DoG)

• Approximates the LoG by subtracting two Gaussian-blurred images: $$DoG=G_{{\sigma }_1}\ast I-G_{{\sigma }_2}\ast I$$
• Faster to compute than LoG.
• Used in blob detection and feature matching.