Convolutional Operations

• Padding
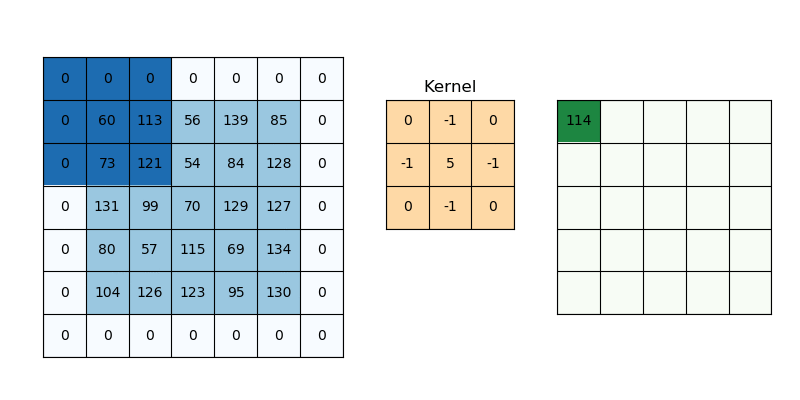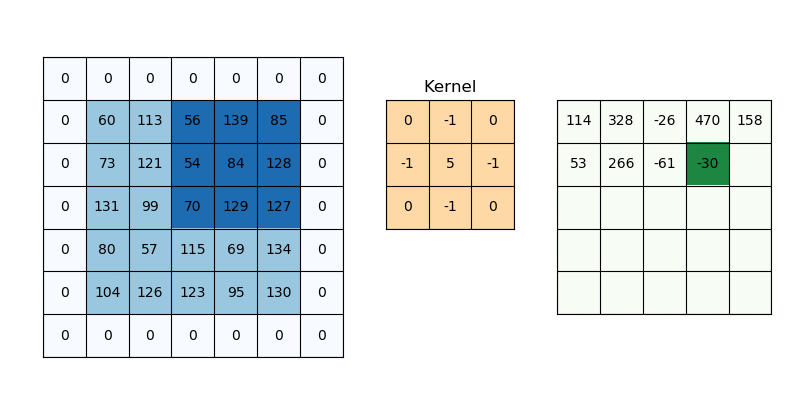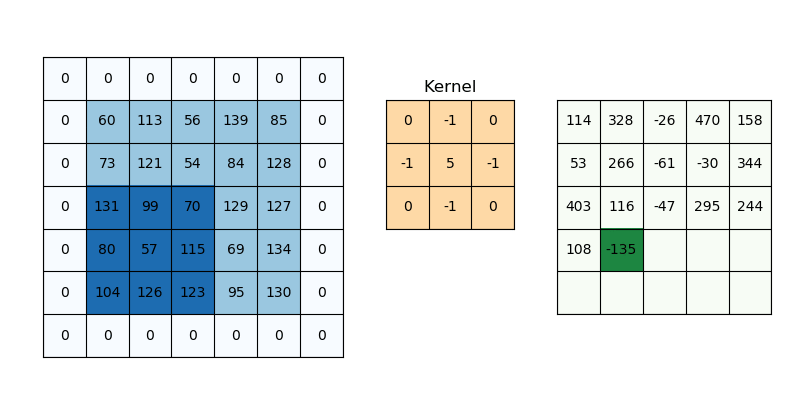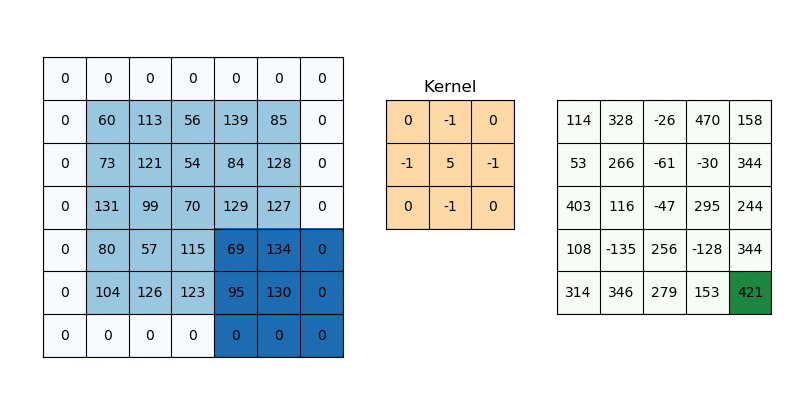
  • Why Padding is Needed
    • Without Padding:
    • With Padding ($p$):
  • Types of Padding
• Strided Convolutions
  • What is Stride?
  • Output Size Formula
• Convolutions Over Volume
  • From 2D to 3D
  • Input Dimensions:
  • Filter Dimensions:
  • Output Volume:
  • Practical Example

Padding

Why Padding is Needed

When applying convolution, the output image shrinks unless we pad it. This is a problem when building deep networks where spatial dimensions shrink after each convolution.

Without Padding:

$$\text{Output size}=n-f+1$$

Where:

• $n$: input size
• $f$: filter size

Example

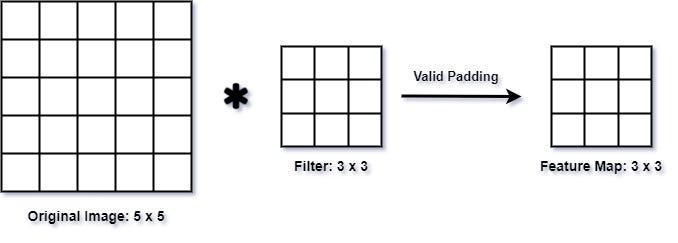
In this image:

• $n$: input size = $5$
• $f$: filter size = $3$

$$\text{Output size}=n-f+1$$

$$\text{Output size}=5-3+1$$

$$\text{Output size}=3$$

With Padding ($p$):

$$\text{Output size}=n+2p-f+1$$

Where:

• $n$: input size
• $f$: filter size
• $p$: padding size

Example

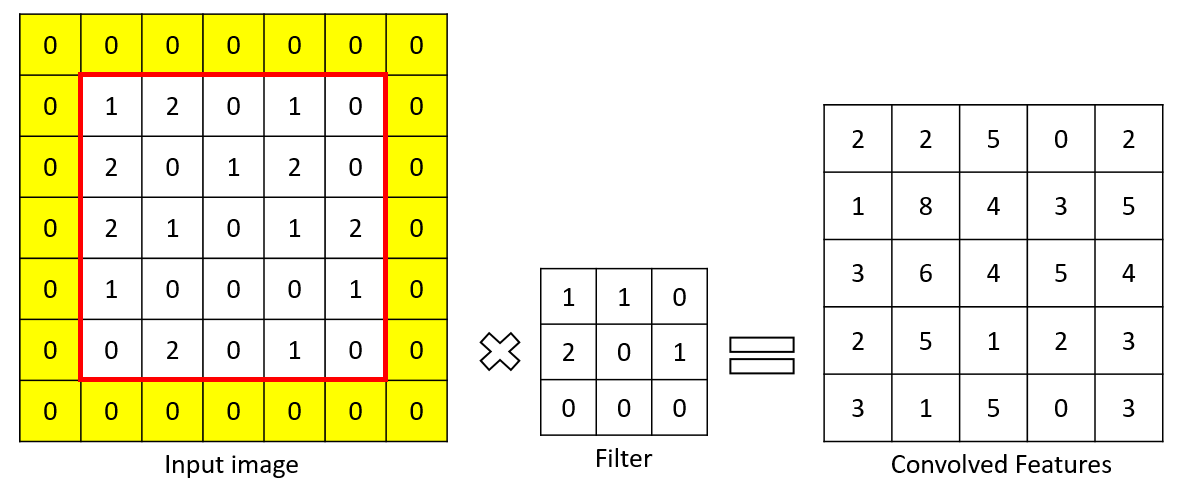
In this image:

• $n$: input size = $6$
• $f$: filter size = $3$
• $p$: padding size = $1$

$$\text{Output size}=n+2p-f+1$$

$$\text{Output size}=6+(2\cdot 1)-3+1$$

$$\text{Output size}=6$$

Types of Padding

• Valid Padding (no padding): Output is smaller.
• Same Padding (zero padding): Output size equals input size.

Real-World Analogy

Imagine scanning a photo with a magnifying glass: without padding, you can’t examine the borders. Padding extends the image so that every pixel gets equal attention.

Strided Convolutions

What is Stride?

Stride is the number of pixels the filter moves at each step.

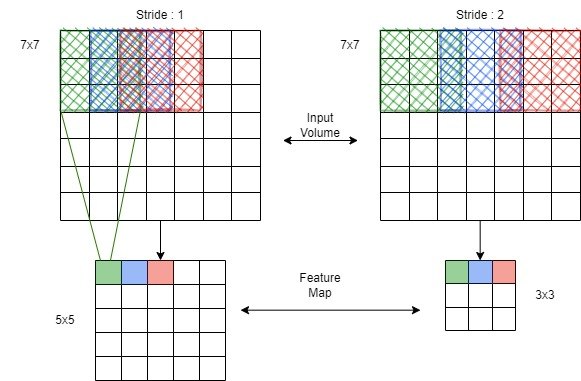
• Stride = 1: Normal convolution (moves 1 pixel at a time)
• Stride = 2: Downsampling (moves 2 pixels at a time)

Output Size Formula

$$\text{Output size}=\lfloor \frac{n+2p-f}{s}\rfloor +1$$

Where:

• $n$: input size
• $f$: filter size
• $s$: stride
• $p$: padding

Visual Example

If stride = 2, the filter skips every alternate pixel, effectively reducing the spatial size of the output.

Convolutions Over Volume

From 2D to 3D

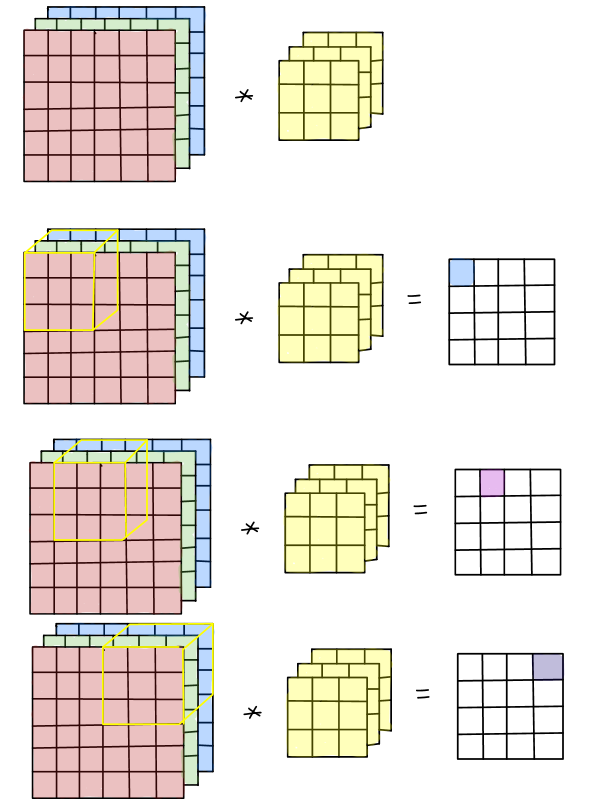
In RGB images, we have 3 channels: Red, Green, and Blue. Thus, a convolutional layer operates over 3D volumes.

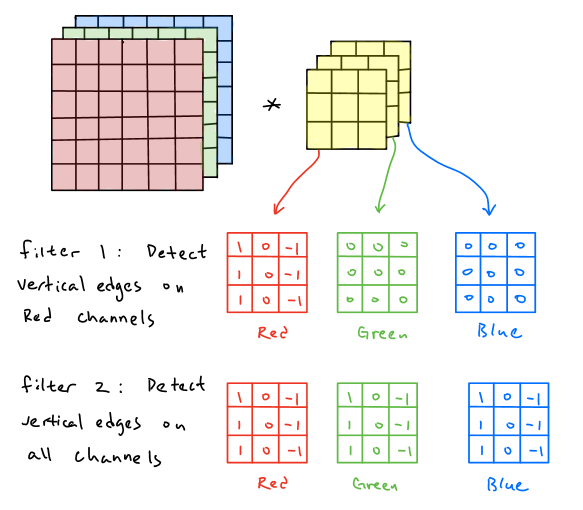
Input Dimensions:

$$(n_H,n_W,n_C)$$

• $n_H$: Height
• $n_W$: Width
• $n_C$: Channels (e.g., 3 for RGB)

Filter Dimensions:

$$(f_H,f_W,n_C)$$

• Number of filters: $n_F$

Output Volume:

$$(n_H^{\prime },n_W^{\prime },n_F)$$

• Each filter creates a 2D activation map, stacked together to form the output volume.

Practical Example

Let’s say you have a (6, 6, 3) image, and you apply 2 filters of size (3, 3, 3):

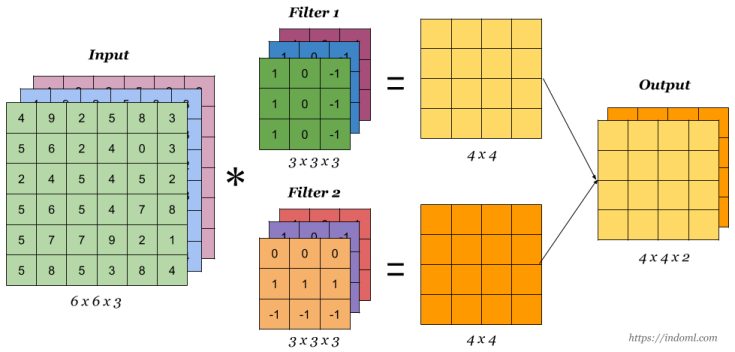
• Output shape: (4, 4, 2) (assuming valid padding, stride=1)