CNN Architecture and Examples
1. One Layer of a Convolutional Network
A Convolutional Neural Network (CNN) is typically composed of three types of layers:
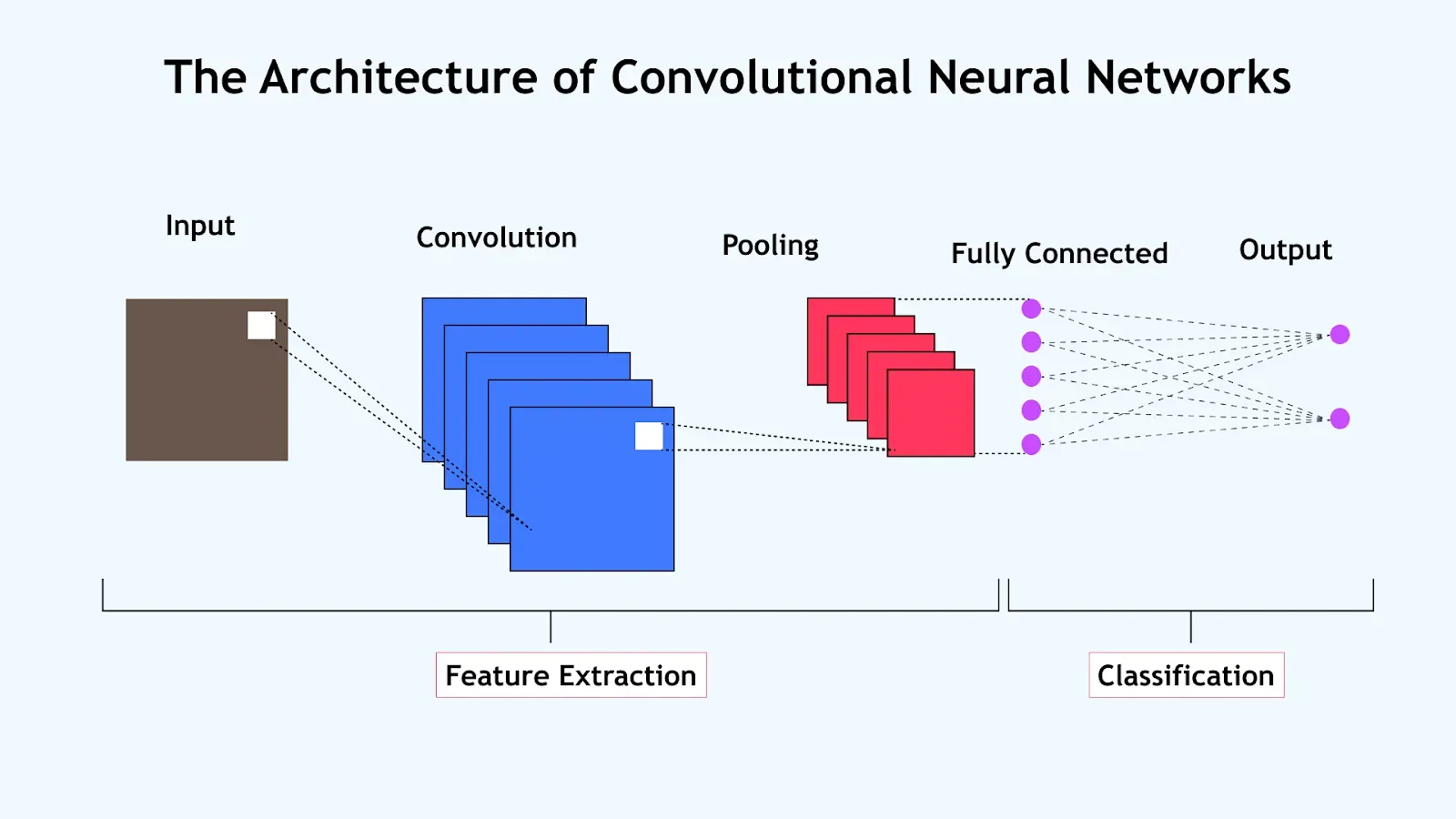
- Convolutional layers: Apply filters to extract spatial features.
- Pooling layers: Downsample feature maps to reduce computation.
- Fully connected layers: Perform final classification or regression.
Each layer transforms the input volume into an output volume through learnable parameters or fixed operations.
Layer Types of CNN
1. Convolutional Layers
Purpose:
To extract spatial features such as edges, textures, and patterns by sliding filters over the input image or feature map.
How it works:
- A filter (or kernel) of size slides over the input.
- At each location, an element-wise multiplication is performed between the filter and the part of the input it overlaps.
- The results are summed to produce a single number in the output feature map.
Mathematical Operation:
Let the input be and the filter be .
Example:
Input: grayscale image with filter:
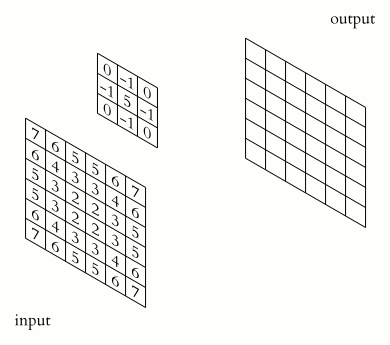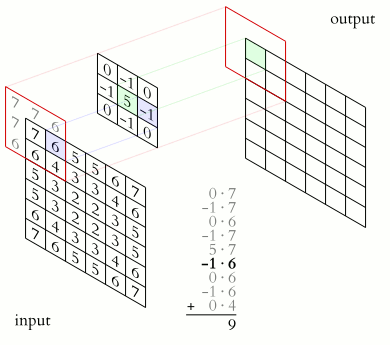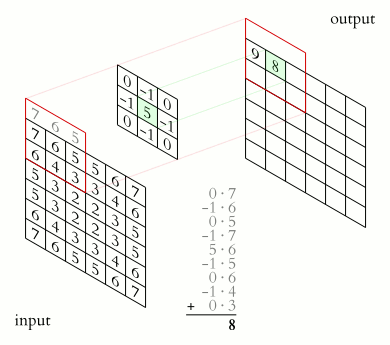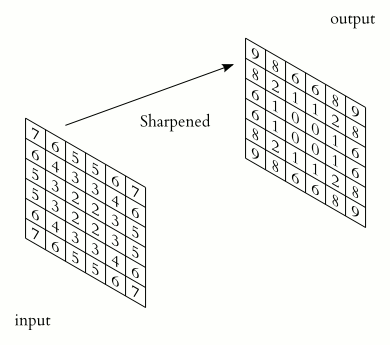
As the filter slides across the input, it detects vertical and horizontal edges by producing high activation in regions with strong center transitions.
2. Pooling Layers
Purpose:
To reduce the spatial dimensions (height and width) of the feature maps, thereby:
- Reducing the number of parameters and computation
- Controlling overfitting
- Making the model invariant to small translations in the input
Types:
Max Pooling:
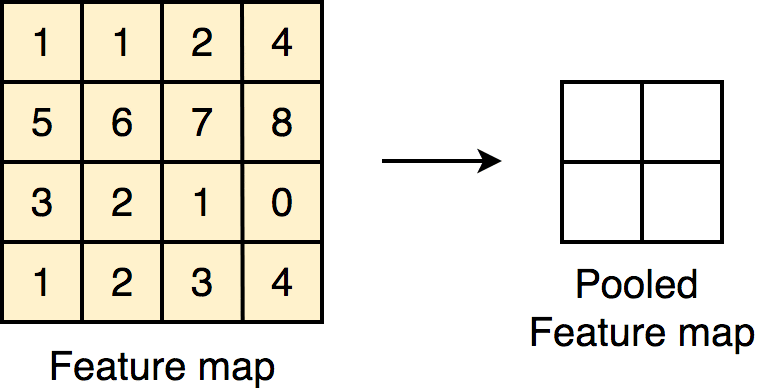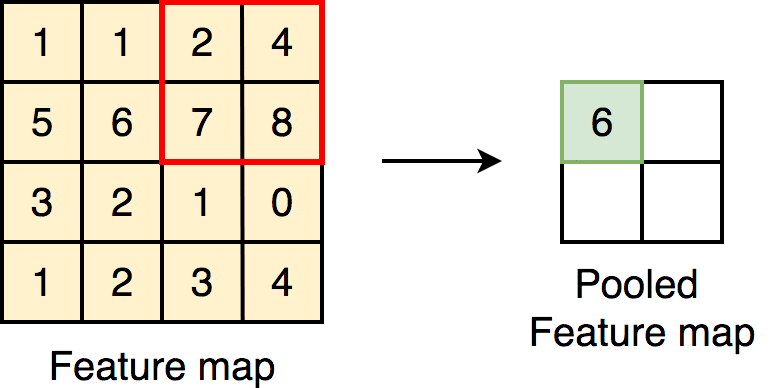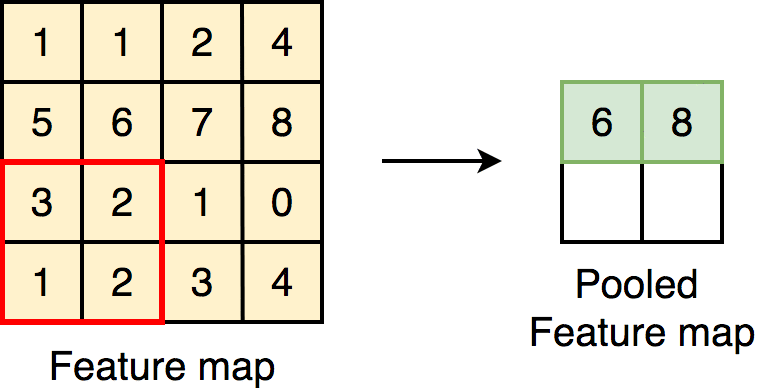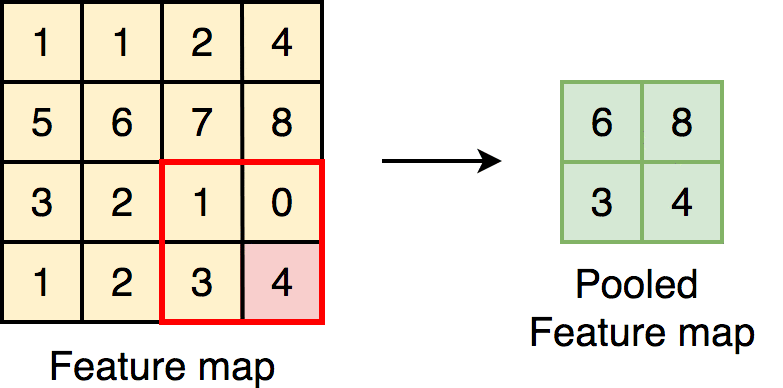
Selects the maximum value in each region.
Average Pooling:
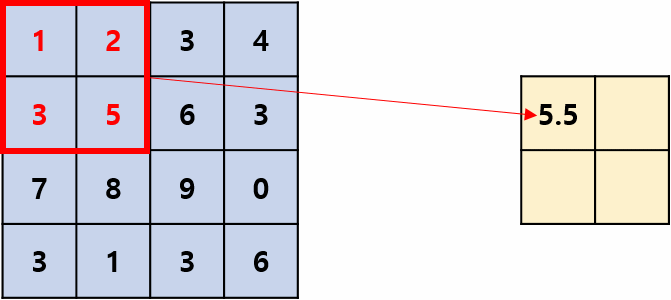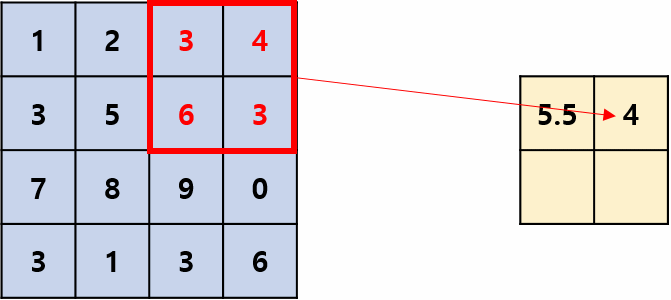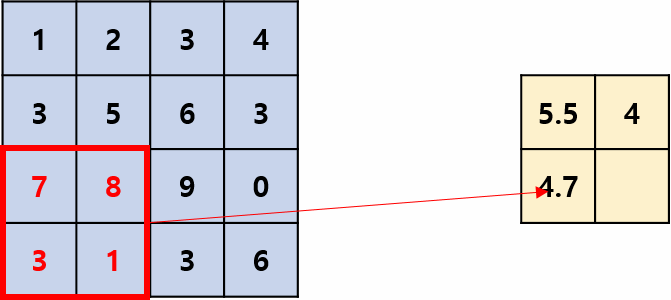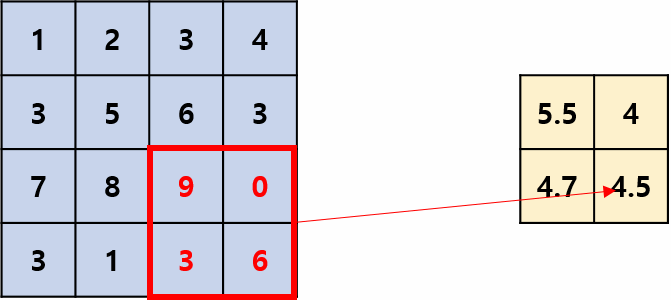
Takes the average of values in each region.
3. Fully Connected Layers
To connect every neuron in one layer to every neuron in the next layer, performing the final classification or regression.
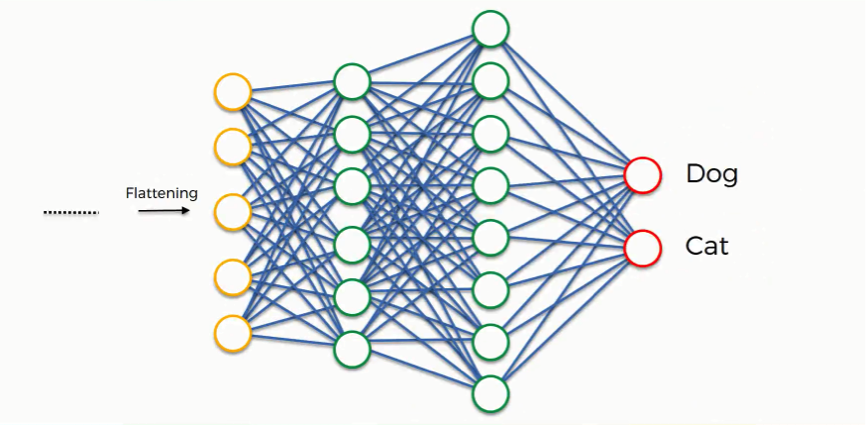
How it works:
- Takes the flattened output from the last convolutional/pooling layer
- Passes it through one or more dense layers
- Final layer often uses softmax for classification
Mathematical Form:
Given the input vector , weights , and bias :
Example:
Let’s say we have a feature map output size of from the last pooling layer:
- FC1: 400 → 120 (ReLU)
- FC2: 120 → 84 (ReLU)
- FC3: 84 → 10 (Softmax, for 10-class classification)
These dense layers combine all the high-level features learned in the earlier layers and output a prediction.
Summary Table
| Layer Type | Role | Typical Parameters | Output Shape Transformation |
|---|---|---|---|
| Convolutional | Extract local spatial features | , , , filters | |
| Pooling | Downsample feature maps | , | |
| Fully Connected | Final classification/regression | neurons per layer | (vector size) |
These layers together form the foundation of Convolutional Neural Networks, enabling them to learn hierarchical representations from raw pixels to abstract concepts.
Notation and Terminology
- : height and width of the input volume
- : number of channels (depth)
- : filter size
- : stride
- : padding
- , : weights and biases at layer
Parameters and Learnable Components
- Weights (): Represent filters; shared spatially across the input.
- Biases (): One per filter.
- Activation (): Output of ReLU or other non-linear function.
Each neuron in a layer is connected only to a small region of the previous layer, leading to sparse interactions and parameter sharing.
3. CNN Example (Comprehensive Network)
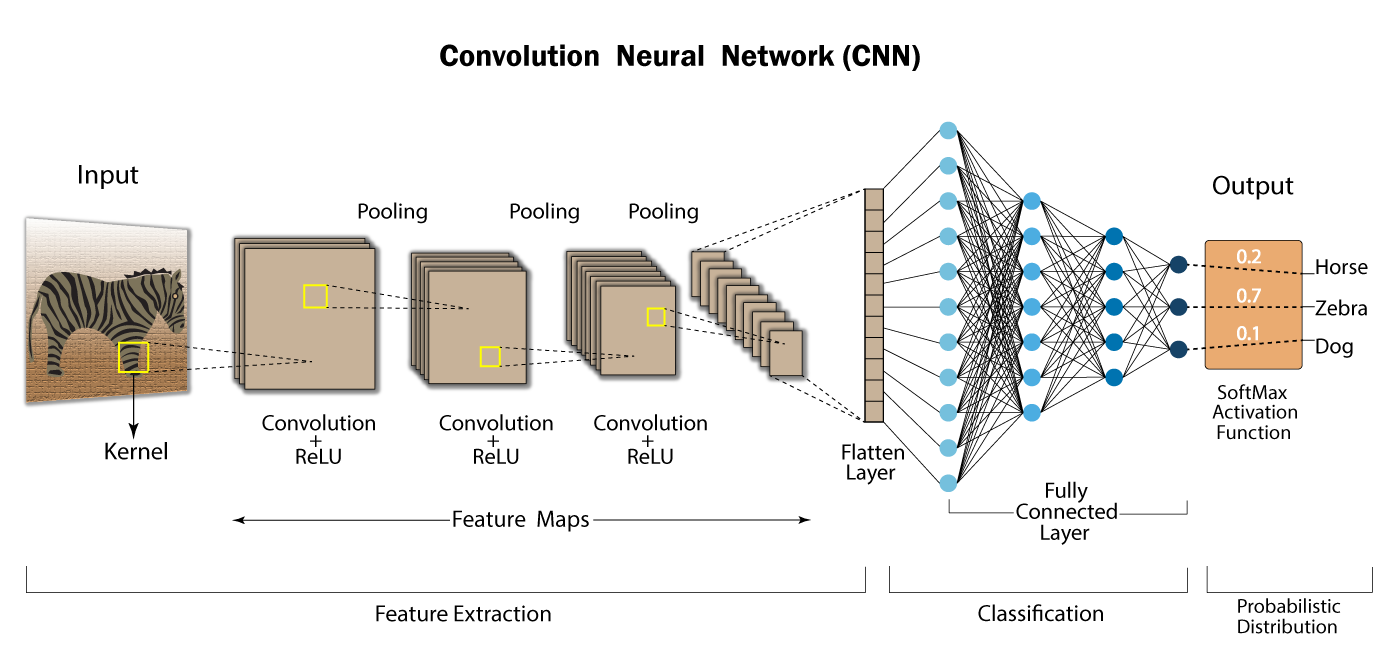
Why Convolutions?
Convolutional layers are the cornerstone of modern deep learning models in computer vision, replacing traditional fully connected layers in image tasks. This section explores why convolutions are used instead of dense layers, and what advantages they bring.
1. The Limitations of Fully Connected Layers for Images
a. Parameter Explosion
A fully connected (dense) layer connecting every pixel of an image to every neuron in the next layer requires a huge number of parameters.
Example:
- Input image size:
- Fully connected layer with 1000 neurons:
This leads to high memory usage, overfitting risk, and long training times.
b. Ignores Spatial Structure
Dense layers treat input features independently and do not take advantage of the spatial locality of image data.
- A cat’s ear in the top-left and bottom-right corners are treated as unrelated by dense layers.
2. Benefits of Convolutional Layers
a. Sparse Interactions
Each output neuron is connected only to a small region of the input (called the receptive field).
- Fewer parameters
- Faster computations
Example:
- Using instead of connecting all 12,288 pixels
b. Parameter Sharing
Same filter (weights) is applied across the entire image:
This results in drastic reduction in number of parameters and allows feature detection to be translation invariant.
c. Translation Equivariance
- If an object moves in the image, its feature map also moves.
- The model learns position-independent features — important for generalization.