Welcome to your-notes.
∴
lorem ipsum dolor sit amet
— your-name
Welcome to Machine Learning notes.
∴
I completed the Machine Learning Specialization Course by taking detailed notes and summarizing critical concepts for future reference.
University of Stanford & DeepLearning.AI
— emreaslan —
Supervised and Unsupervised Machine Learning
Introduction
Machine learning is a branch of artificial intelligence that allows systems to learn and make predictions or decisions without explicit programming. Two main types of machine learning are Supervised Learning and Unsupervised Learning. Below is a summary of their characteristics, subfields, along with a visual representation for clarity.
graph TD
A[Machine Learning] --> B[Supervised Learning]
A --> C[Unsupervised Learning]
B --> D[Regression]
B --> E[Classification]
C --> F[Clustering]
C --> G[Association]
C --> H[Dimensionality Reduction]
Supervised Learning
Supervised learning is a type of machine learning where the model is trained on labeled data. Labeled data means that each input has a corresponding output (or target) already provided. The goal is for the model to learn the relationship between the inputs and outputs so that it can make predictions for new, unseen data.
Key Characteristics
- Input and Output: The training data contains both input features (X) and target labels (Y).
- Goal: Predict the output (Y) for a given input (X).
Subfields
- Regression: Predicting continuous values (e.g., predicting rent prices based on apartment size).
- Classification: Assigning inputs to discrete categories (e.g., diagnosing cancer as benign or malignant).
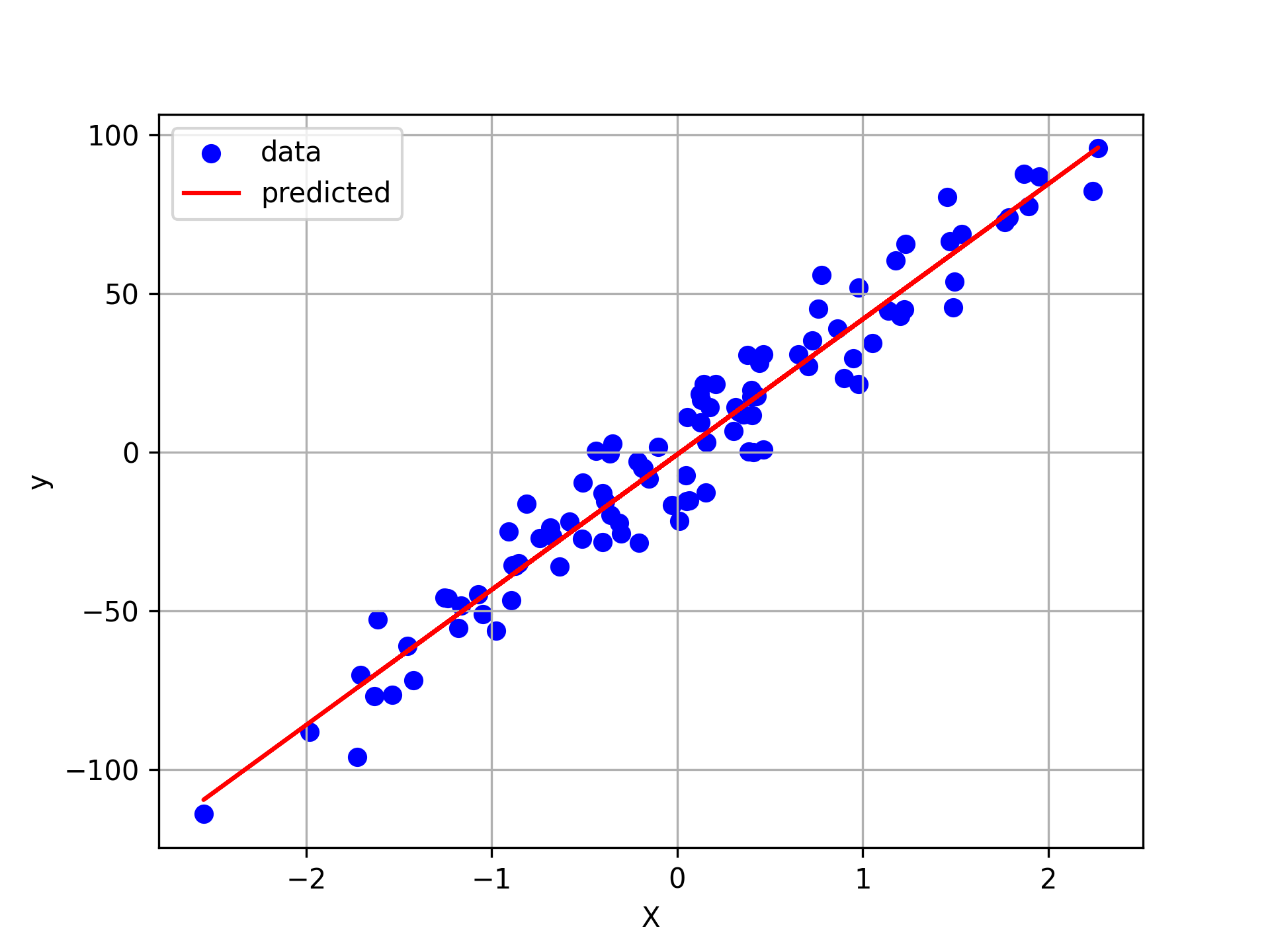
Example: Regression
- Scenario: Predicting rent prices based on apartment size (in m²).
- Details:
- Input features (X): Apartment size, number of rooms, neighborhood, etc.
- Target variable (Y): Rent price (e.g., $ per month).
- Model's Job: Learn the relationship between apartment features and rent prices, then predict the rent for a new apartment.
Example: Classification
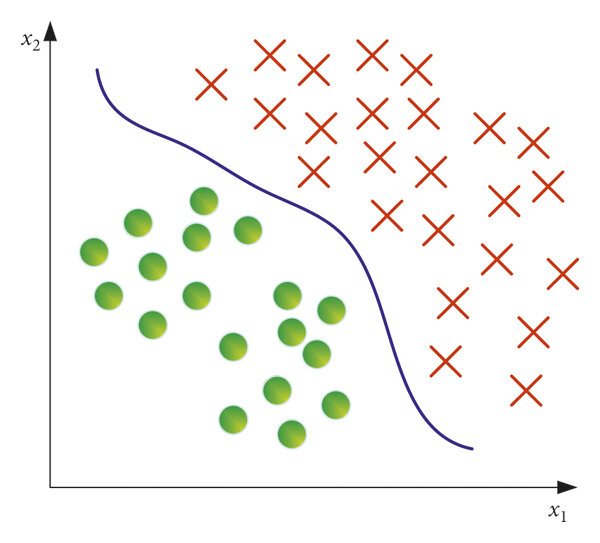
- Scenario: Diagnosing cancer (e.g., benign or malignant tumor).
- Details:
- Input features (X): Measurements like tumor size, texture, cell shape, etc.
- Target variable (Y): Class label (e.g., "Benign" or "Malignant").
- Model's Job: Classify a new tumor as benign or malignant based on input features.
Unsupervised Learning
Unsupervised learning deals with unlabeled data. The model tries to find patterns, structures, or relationships within the data without any predefined labels or targets. It’s often used for exploratory data analysis.
Key Characteristics
- Input Only: The data contains only input features (X), with no target labels (Y).
- Goal: Discover hidden patterns or groupings in the data.
Subfields
- Clustering: Grouping similar data points into clusters (e.g., customer segmentation).
- Dimensionality Reduction: Reducing the number of features in the dataset while preserving important information (e.g., PCA).
- Association: Discovering relationships or associations between variables in large datasets (e.g., market basket analysis).
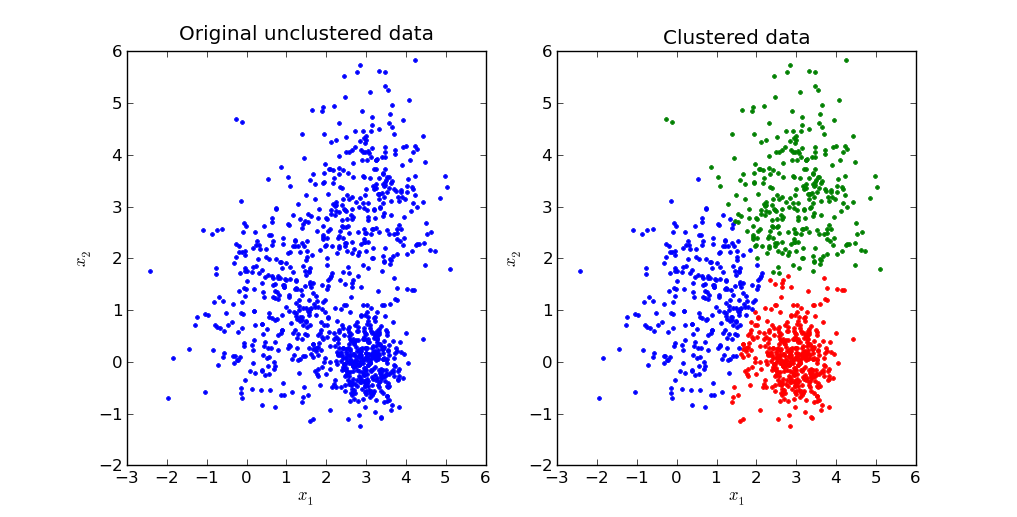
Example: Clustering
- Scenario: Grouping customers for targeted marketing.
- Details:
- Input features (X): Customer age, income, purchase history, location, etc.
- No predefined labels (Y).
- Model's Job: Identify clusters of customers (e.g., "High-spenders," "Budget-conscious buyers").
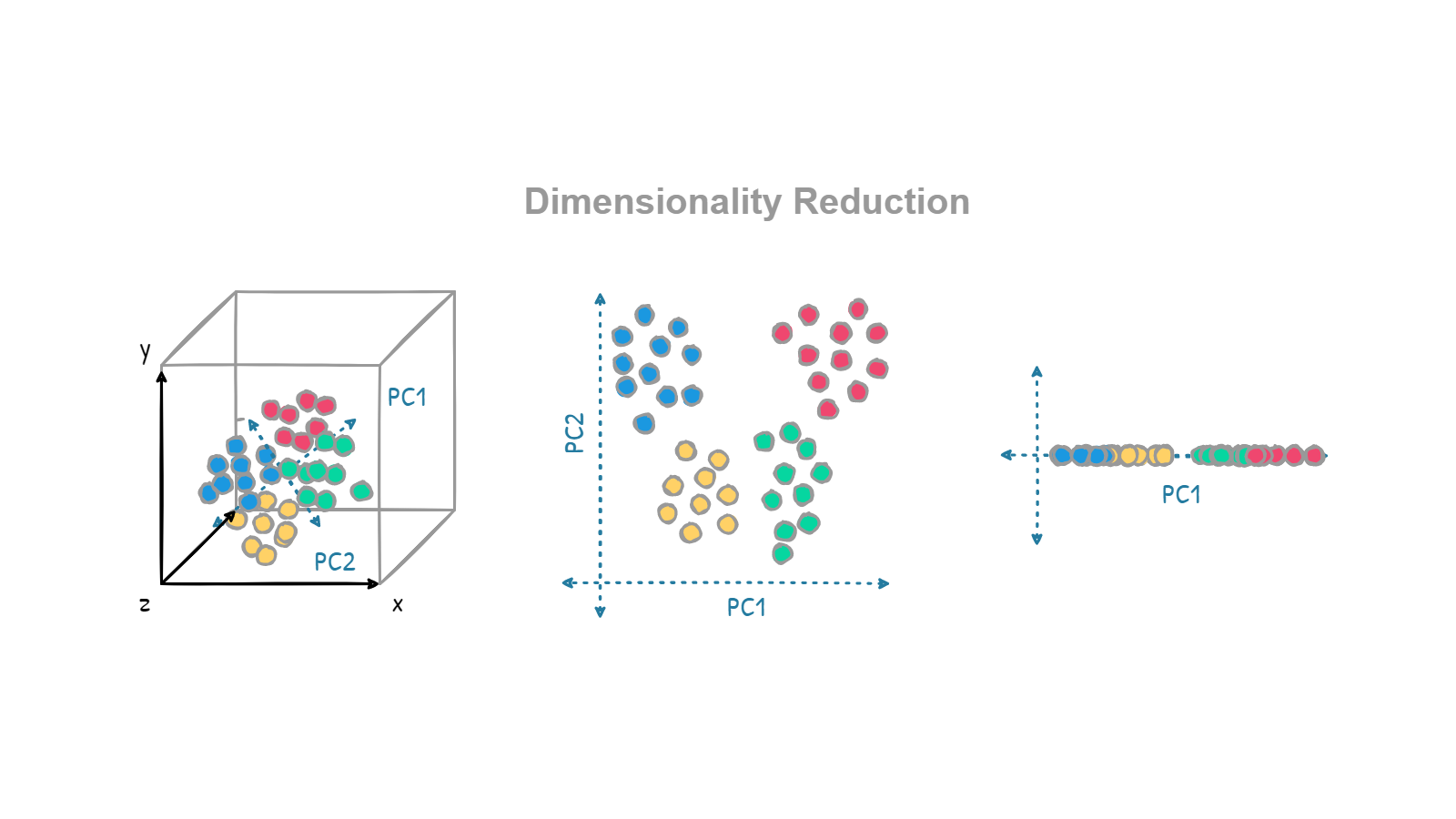
Example: Dimensionality Reduction
- Scenario: Visualizing high-dimensional data.
- Details:
- Imagine you have a dataset with 100+ features (e.g., sensor data from a factory).
- Dimensionality reduction (e.g., PCA) helps reduce it to 2D or 3D for easier visualization.
- Model's Job: Keep the important structure of the data while reducing complexity.
Example: Association
- Scenario: Market basket analysis to identify product associations.
- Details:
- Input features (X): Transaction data showing items purchased together.
- No predefined labels (Y).
- Model's Job: Identify rules like "If a customer buys bread, they are likely to buy butter."
- Use Case: Recommendation systems, inventory planning.
Comparison Table
| Feature | Supervised Learning | Unsupervised Learning |
|---|---|---|
| Data Type | Labeled data (X, Y) | Unlabeled data (X only) |
| Goal | Predict outcomes | Find patterns or structures |
| Key Techniques | Regression, Classification | Clustering, Dimensionality Reduction, Assocation |
| Examples | Fraud detection, Stock price prediction | Market segmentation, Image compression |
Key Takeaways
- Supervised Learning requires labeled data and is commonly used for prediction tasks like regression and classification.
- Unsupervised Learning works with unlabeled data and focuses on finding hidden patterns through clustering or dimensionality reduction.
- Each technique has specific applications and is chosen based on the problem and the data available.
- Linear Regression and Cost Function
Linear Regression and Cost Function
1. Introduction
Linear regression is one of the fundamental algorithms in machine learning. It is widely used for predictive modeling, especially when the relationship between the input and output variables is assumed to be linear. The primary goal is to find the best-fitting line that minimizes the error between predicted values and actual values.
Why Linear Regression?
Linear regression is simple yet powerful for many real-world applications. Some common use cases include:
- Predicting house prices based on features like size, number of rooms, and location.
- Estimating salaries based on experience, education level, and industry.
- Understanding trends in various fields like finance, healthcare, and economics.
Real-World Example: Housing Prices
Consider predicting house prices based on the size of the house (in square meters). A simple linear relationship can be assumed: larger houses tend to have higher prices. This assumption is the foundation of our linear regression model.
2. Mathematical Representation
A simple linear regression model assumes a linear relationship between the input (house size in square meters) and the output (house price). It is represented as:
where:
- is the predicted house price.
- (intercept) and (slope) are the parameters of the model.
- is the house size.
- is the actual house price.
2.1 Understanding the Linear Model
But what does this equation really mean?
-
(intercept): The price of a house when its size is 0 m².
-
(slope): The increase in house price for every additional square meter.
For example, if:
-
and ,
-
A 100 m² house would cost:
-
A 200 m² house would cost:
We can visualize this relationship using a regression line.
3. Implementing Linear Regression Step by Step
To make the theoretical concepts clearer, let's implement the regression model step by step using Python.
3.1 Import Necessary Libraries
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
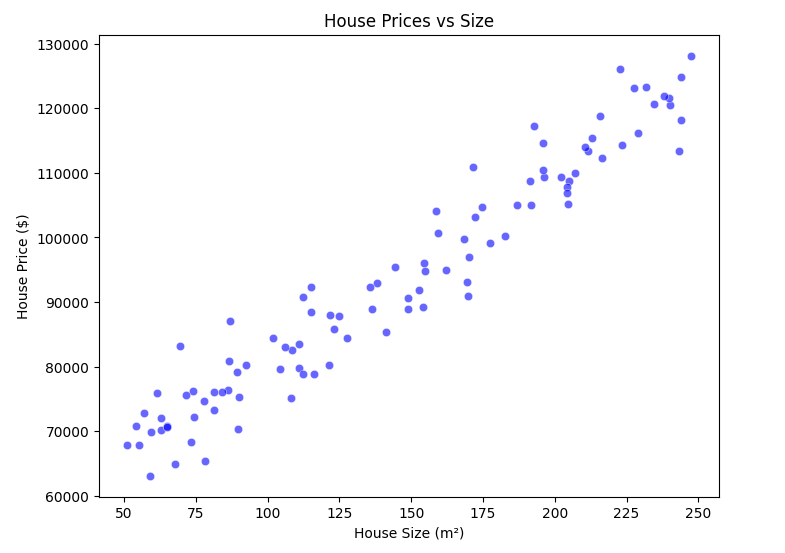
3.2 Generate Sample Data
np.random.seed(42)
x = 50 + 200 * np.random.rand(100, 1) # House sizes in m² (50 to 250)
y = 50000 + 300 * x + np.random.randn(100, 1) * 5000 # House prices with noise
Here, we create a dataset with 100 samples, where:
-
represents house sizes (random values between and m²).
-
represents house prices, following a linear relation but with some noise.
3.3 Visualizing the Data
plt.figure(figsize=(8,6))
sns.scatterplot(x=x.flatten(), y=y.flatten(), color='blue', alpha=0.6)
plt.xlabel('House Size (m²)')
plt.ylabel('House Price ($)')
plt.title('House Prices vs Size')
plt.show()
3.4 Plotting the Regression Line
Before moving to cost function, let's fit a simple regression line to our data and visualize it.
In real-world applications, we don't manually compute these parameters. Instead, we use libraries like scikit-learn to perform linear regression efficiently.
3.4.1 Compute the Slope ()
theta_1 = np.sum((x - np.mean(x)) * (y - np.mean(y))) / np.sum((x - np.mean(x))**2)
Here, we compute the slope () using the least squares method.
3.4.2 Compute the Intercept ()
theta_0 = np.mean(y) - theta_1 * np.mean(x)
This calculates the intercept (), ensuring that our regression line passes through the mean of the data.
3.5 Plotting the Regression Line
y_pred = theta_0 + theta_1 * x # Compute predicted values
plt.figure(figsize=(8,6))
sns.scatterplot(x=x.flatten(), y=y.flatten(), color='blue', alpha=0.6, label='Actual Data')
plt.plot(x, y_pred, color='red', linewidth=2, label='Regression Line')
plt.xlabel('House Size (m²)')
plt.ylabel('House Price ($)')
plt.title('Linear Regression Model: House Prices vs. Size')
plt.legend()
plt.show()
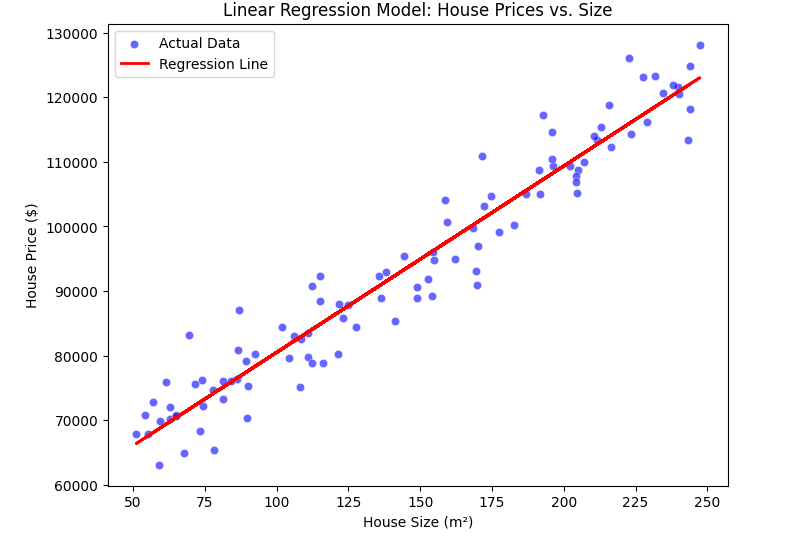
3.6 Interpretation of the Regression Line
Now, what does this line tell us?
✅ If the slope is positive, then larger houses cost more (as expected).
✅ If the intercept is high, it means even the smallest houses have a significant base price.
✅ The steepness of the line shows how much price increases per square meter.
4. Cost Function
To measure how well our model is performing, we use the cost function. The most common cost function for linear regression is the Mean Squared Error (MSE):
where:
- is the number of training examples.
- is the predicted price for the house.
- is the actual price.
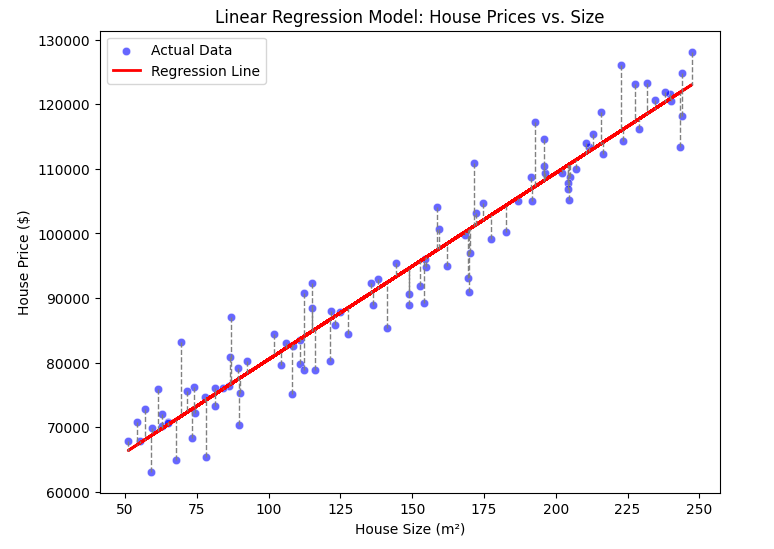
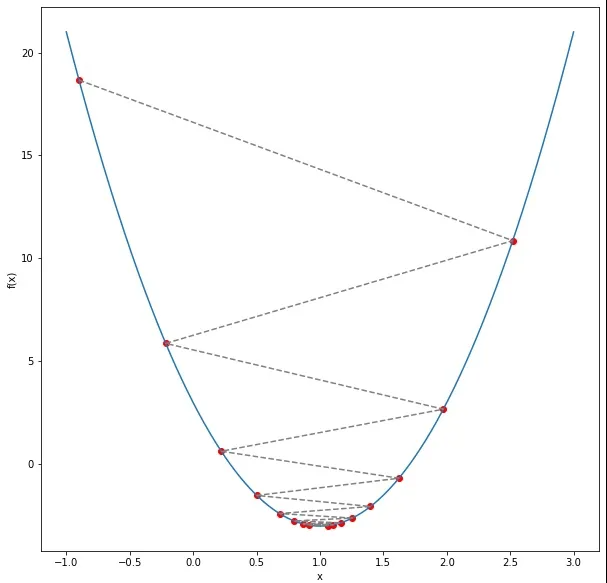
Any dashed line indicates an error. In the formula above, we calculated the sum of these, namely .
This function calculates the average squared difference between predicted and actual values, penalizing larger errors more. The goal is to minimize to achieve the best model parameters.
4.1 Example: Assuming
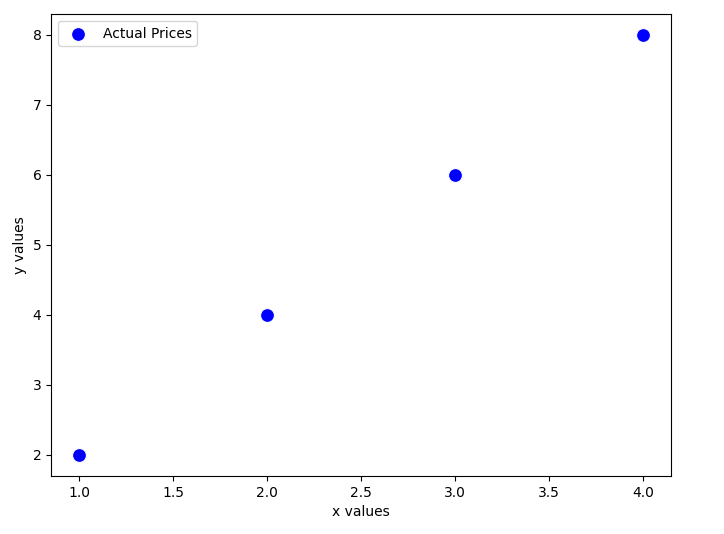
To illustrate how the cost function behaves, let's assume that , meaning our model only depends on . We'll use a small dataset with four x values and y values:
| x values | y values |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
Since we assume , our hypothesis function simplifies to:
We'll evaluate different values of and compute the corresponding cost function.
Case 1:
For , the predicted values are:
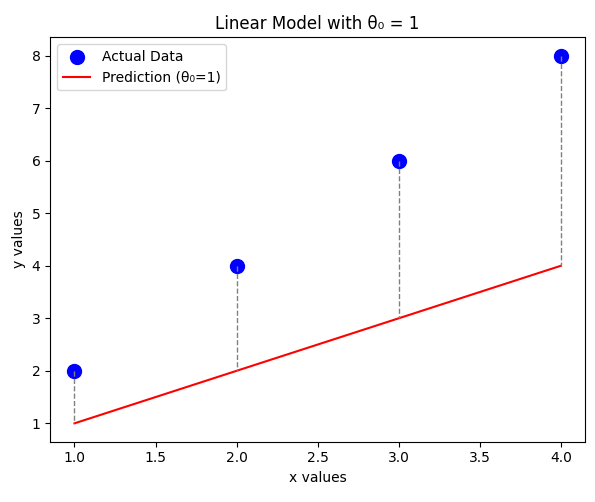
The error values:
Computing the cost function:
Case 2:
For , the predicted values are:
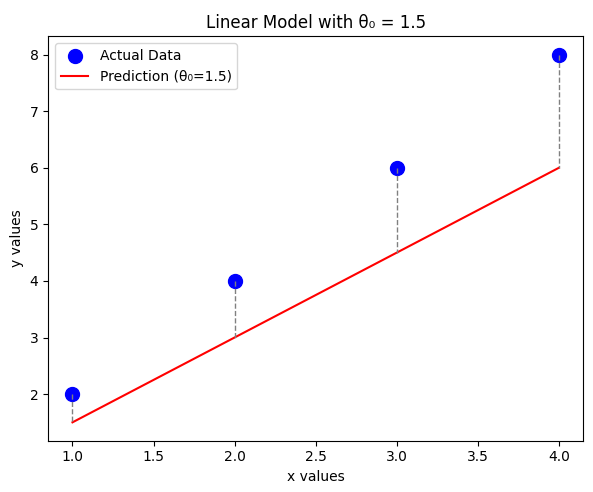
The error values:
Computing the cost function:
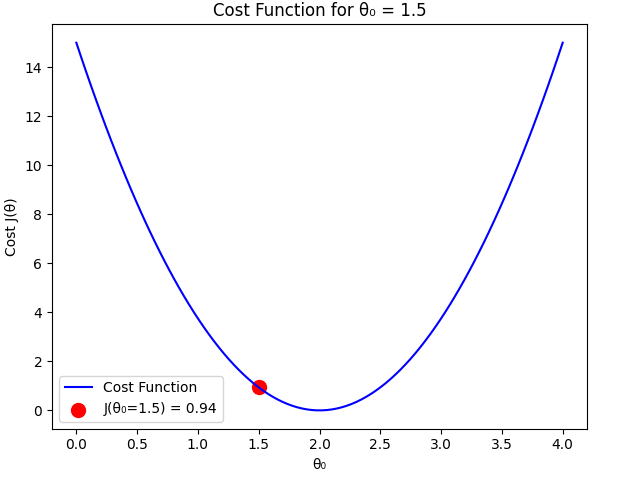
Case 3: (Optimal Case)
For , the predicted values match the actual values:
The error values:
Computing the cost function:
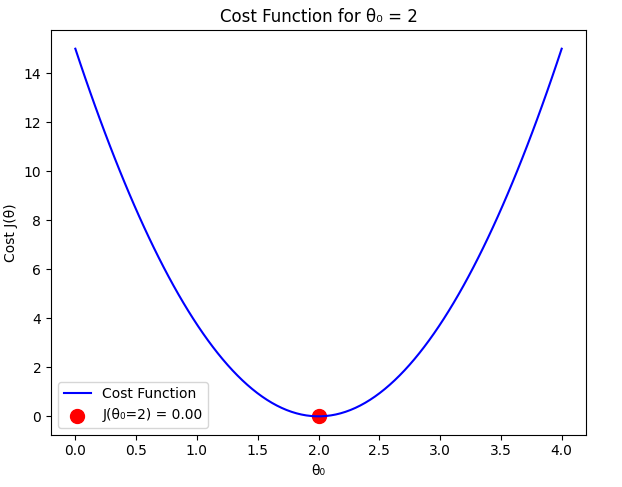
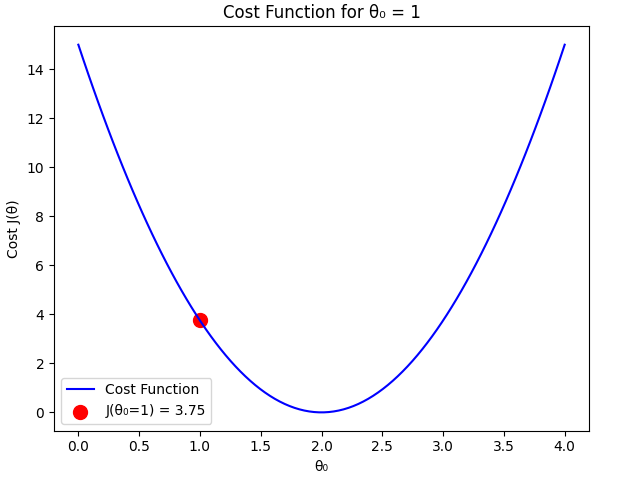
Comparison
From our calculations:
As expected, the cost function is minimized when , which perfectly fits the dataset. Any deviation from this value results in a higher cost.
So how many times can the machine try and find the correct value? How can we teach it this? The answer is in the next topic.
- Introduction to Gradient Descent
- Mathematical Formulation of Gradient Descent
- Learning Rate ()
- Gradient Descent Convergence
- Local Minimum vs Global Minimum
Introduction to Gradient Descent
In the previous section, we explored how the cost function behaves when assuming different values of with (To visualize it easily, we give zero to ). Now, we introduce Gradient Descent, an optimization algorithm used to find the best parameters that minimize the cost function .
our hypothesis function simplifies to:
Gradient Descent is an iterative method that updates the parameter step by step in the direction that reduces the cost function. The algorithm helps us find the optimal value of efficiently instead of manually testing different values.
To understand how Gradient Descent works, let's recall our dataset:
| x values | y values |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |

We aim to find the best value of that minimizes the error between our predictions and the actual values. Gradient Descent will iteratively adjust to reach the minimum cost.
Mathematical Formulation of Gradient Descent
Gradient Descent is an optimization algorithm used to minimize a function by iteratively updating its parameters in the direction of the steepest descent. In our case, we aim to minimize the cost function:
Where:
- 𝑚 is the number of training examples.
- represents our hypothesis function (predicted values).
- y represents the actual target values.
- Goal: Find the optimal that minimizes .
1. Gradient Descent Update Rule
Gradient Descent uses the derivative of the cost function to determine the direction and magnitude of updates. The general update rule for is:
Where:
- (learning rate) controls the step size of updates.
- is the gradient (derivative) of the cost function with respect to .
Why Do We Use the Derivative?
The derivative tells us the slope of the cost function. If the slope is positive, we need to decrease , and if it is negative, we need to increase , guiding us toward the minimum of . Without derivatives, we wouldn't know which direction to move to minimize the function.
The gradient tells us how steeply the function increases or decreases at a given point.
- If the gradient is positive, is decreased.
- If the gradient is negative, is increased.
This ensures that we move toward the minimum of the cost function.
2. Computing the Gradient
First, recall our hypothesis function:
Now, we compute the derivative of the cost function:
This expression represents the average gradient of the errors multiplied by the input values. Using this gradient, we update in each iteration:
- If the error is large, the update step is bigger.
- If the error is small, the update step is smaller.
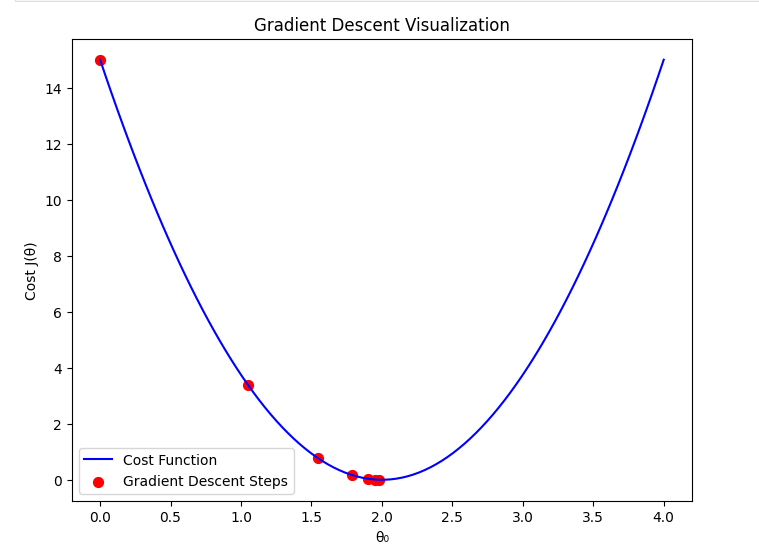
This way, the algorithm gradually moves towards the optimal .
Learning Rate ()
The learning rate is a crucial parameter in the gradient descent algorithm. It determines how large a step we take in the direction of the negative gradient during each iteration. Choosing an appropriate learning rate is essential for ensuring efficient convergence of the algorithm.
If the learning rate is too small, the algorithm will take tiny steps towards the minimum, leading to slow convergence. On the other hand, if the learning rate is too large, the algorithm may overshoot the minimum or even diverge, never reaching an optimal solution.
1. When is Too Small
If the learning rate is set too small:
- Gradient descent will take very small steps in each iteration.
- Convergence to the minimum cost will be extremely slow.
- It may take a large number of iterations to reach a useful solution.
- The algorithm might get stuck in local variations of the cost function, slowing down learning.
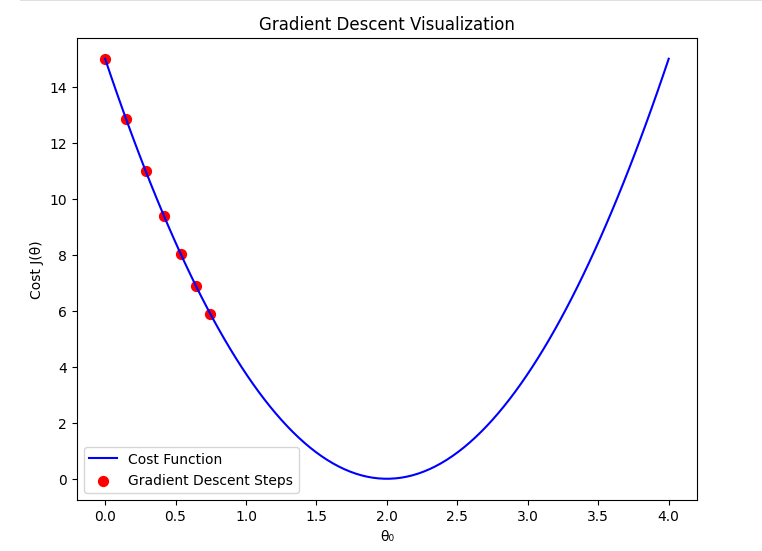
Mathematically, the update rule is: When is very small, the change in per step is minimal, making the process inefficient.
2. When is Optimal
If the learning rate is chosen optimally:
- The gradient descent algorithm moves efficiently towards the minimum.
- It balances speed and stability, converging in a reasonable number of iterations.
- The cost function decreases steadily without oscillations or divergence.

A well-chosen ensures that gradient descent follows a smooth and steady path to the minimum.
3. When is Too Large
If the learning rate is set too large:
- Gradient descent may take excessively large steps.
- Instead of converging, it may oscillate around the minimum or diverge entirely.
- The cost function might increase instead of decreasing due to overshooting the optimal .
In extreme cases, the cost function values might increase indefinitely, causing the algorithm to fail to find a minimum.
Summary
Selecting the right learning rate is essential for gradient descent to work efficiently. A well-balanced ensures that the algorithm converges quickly and effectively. In the next section, we will implement gradient descent with different learning rates to visualize their effects.
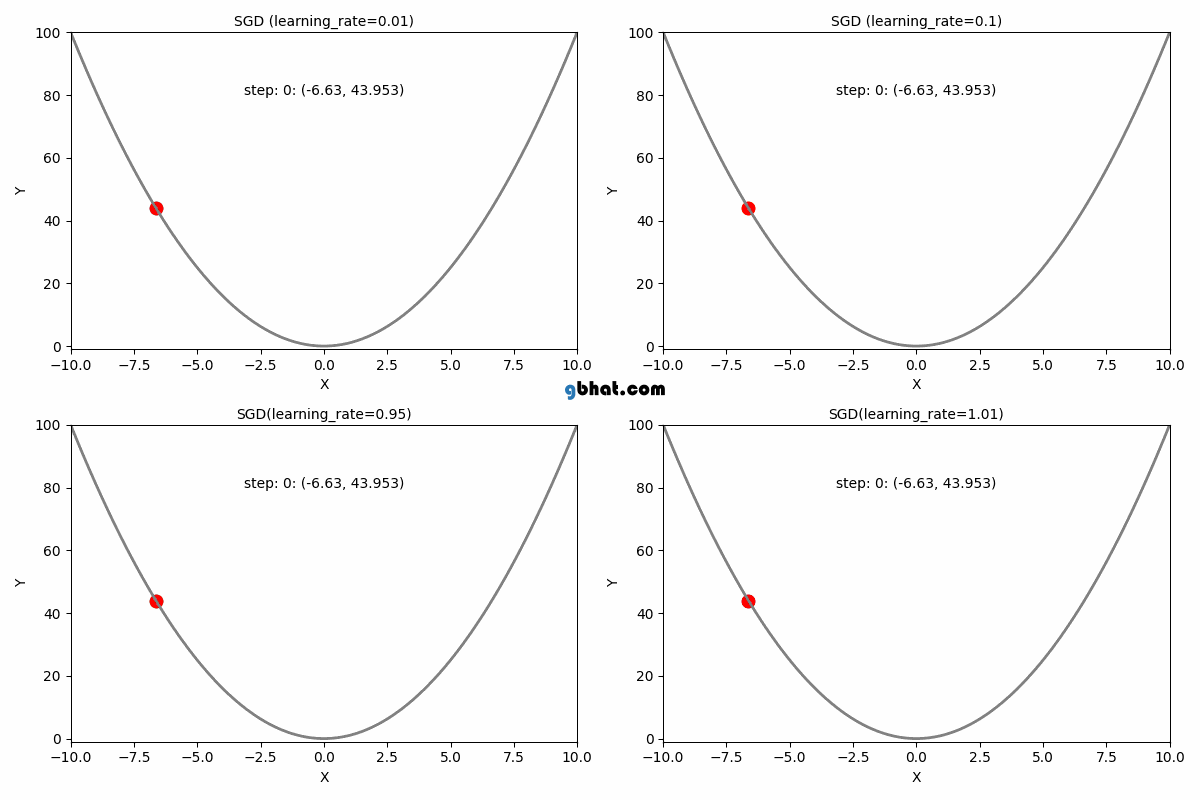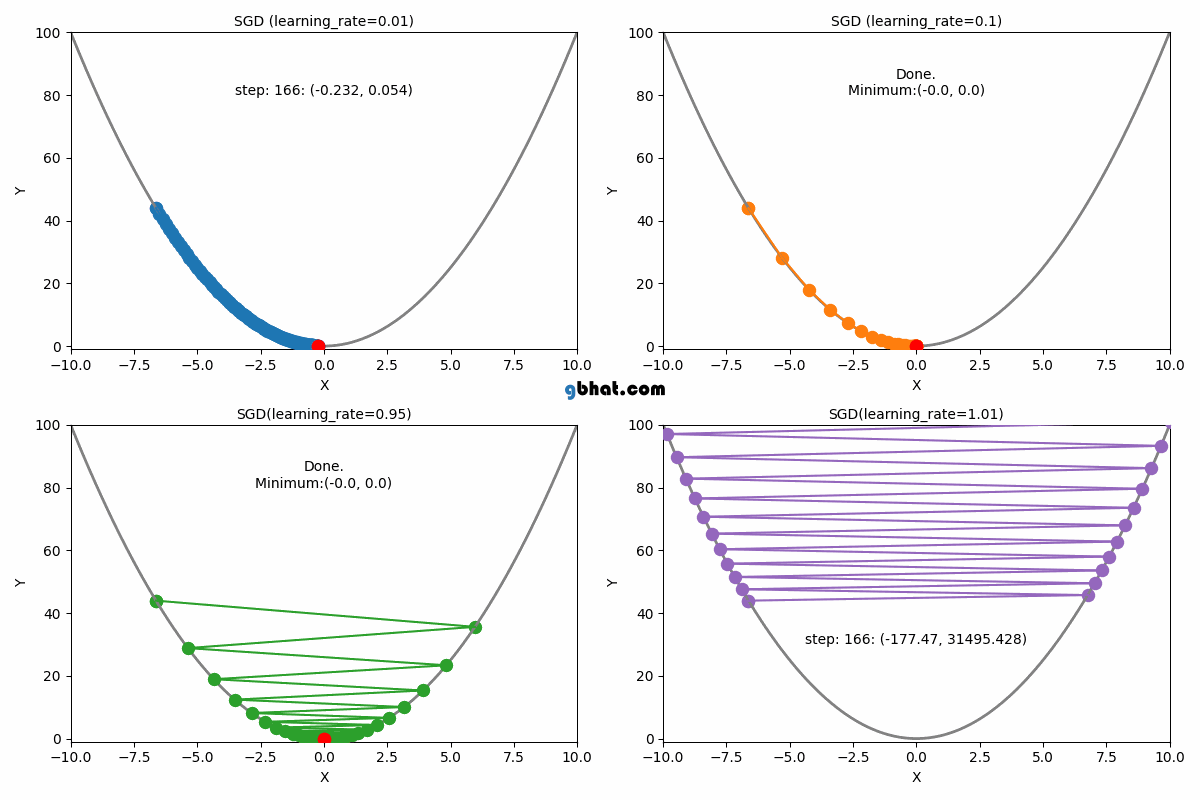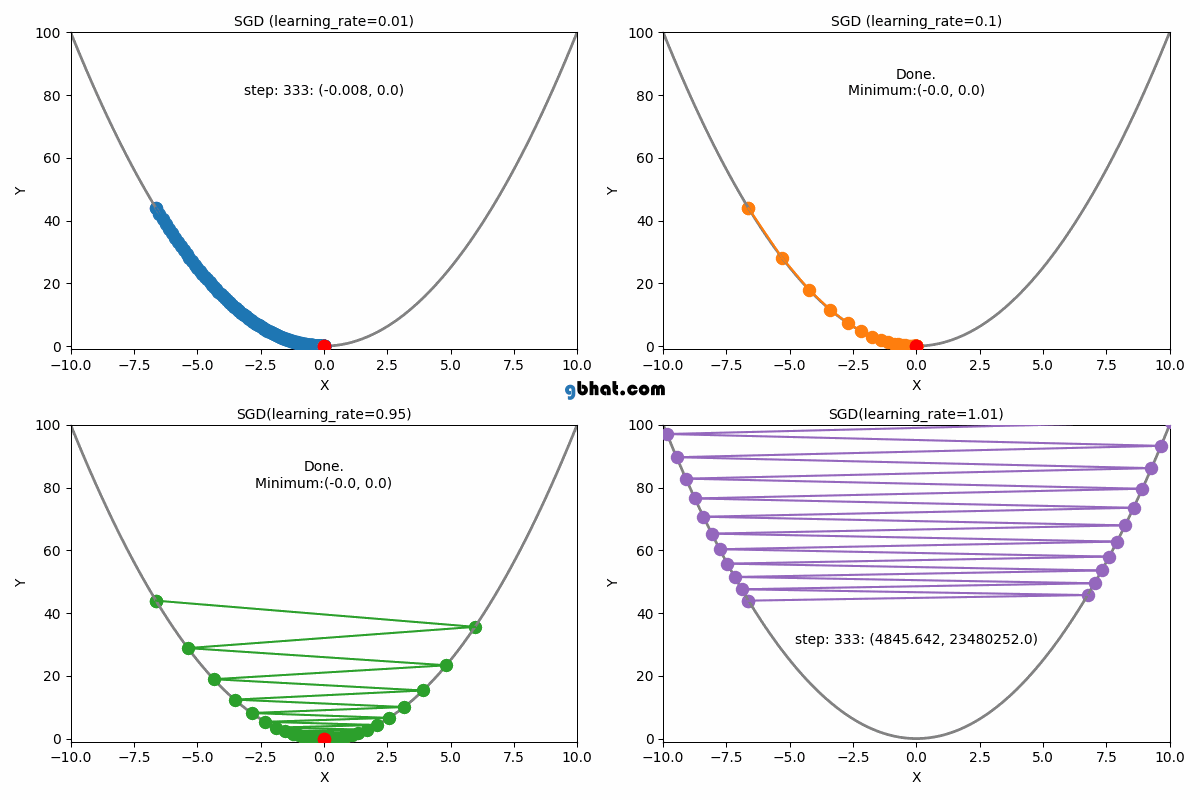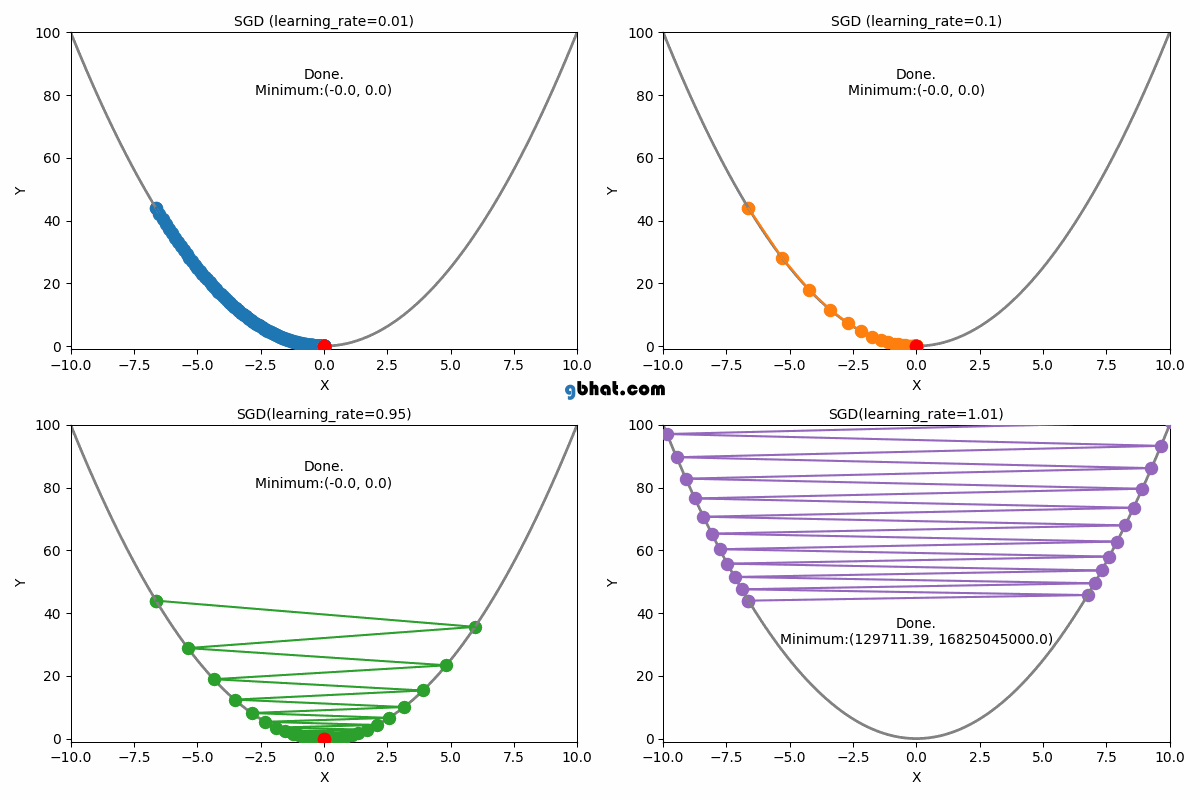
Gradient Descent Convergence
Gradient Descent is an iterative optimization algorithm that minimizes the cost function, J(\theta), by updating parameters step by step. However, we need a proper stopping criterion to determine when the algorithm has converged.
1. Convergence Criteria
The algorithm should stop when one of the following conditions is met:
- Small Gradient: If the derivative (gradient) of the cost function is close to zero, meaning the algorithm is near the optimal point.
- Minimal Cost Change: If the difference in the cost function between iterations is below a predefined threshold ().
- Maximum Iterations: A fixed number of iterations is reached to avoid infinite loops.
2. Choosing the Right Stopping Condition
- Stopping Too Early: If the algorithm stops before reaching the optimal solution, the model may not perform well.
- Stopping Too Late: Running too many iterations may waste computational resources without significant improvement.
- Optimal Stopping: The best condition is when further updates do not significantly change the cost function or parameters.
Local Minimum vs Global Minimum
Understanding the Concept
When optimizing a function, we aim to find the point where the function reaches its lowest value. This is crucial in machine learning because we want to minimize the cost function effectively. However, there are two types of minima that gradient descent might encounter:
- Global Minimum: The absolute lowest point of the function. Ideally, gradient descent should converge here.
- Local Minimum: A point where the function has a lower value than nearby points but is not the absolute lowest value.
For convex functions (such as our quadratic cost function), gradient descent is guaranteed to reach the global minimum. However, for non-convex functions, the algorithm may get stuck in a local minimum.
Convex vs Non-Convex Cost Functions
- Convex Functions
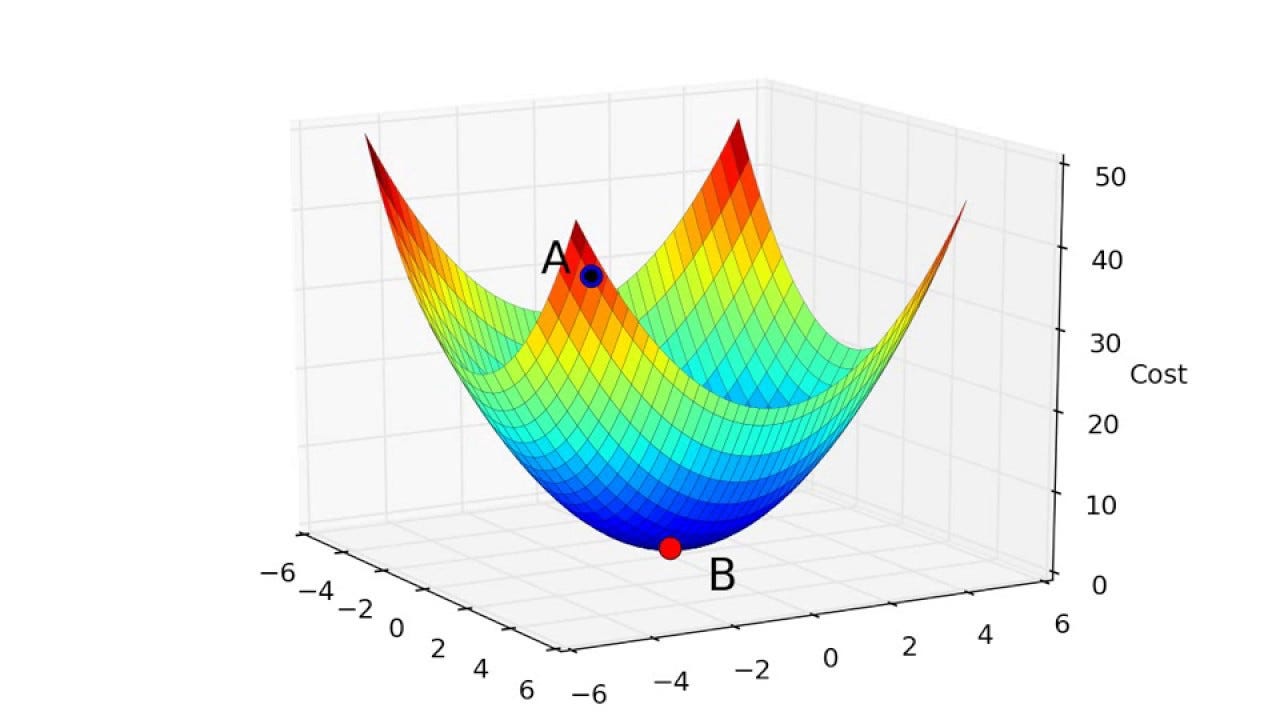
- The cost function is convex for linear regression.
- This ensures that gradient descent always leads to the global minimum.
- Example: A simple quadratic function like .
- Non-Convex Functions
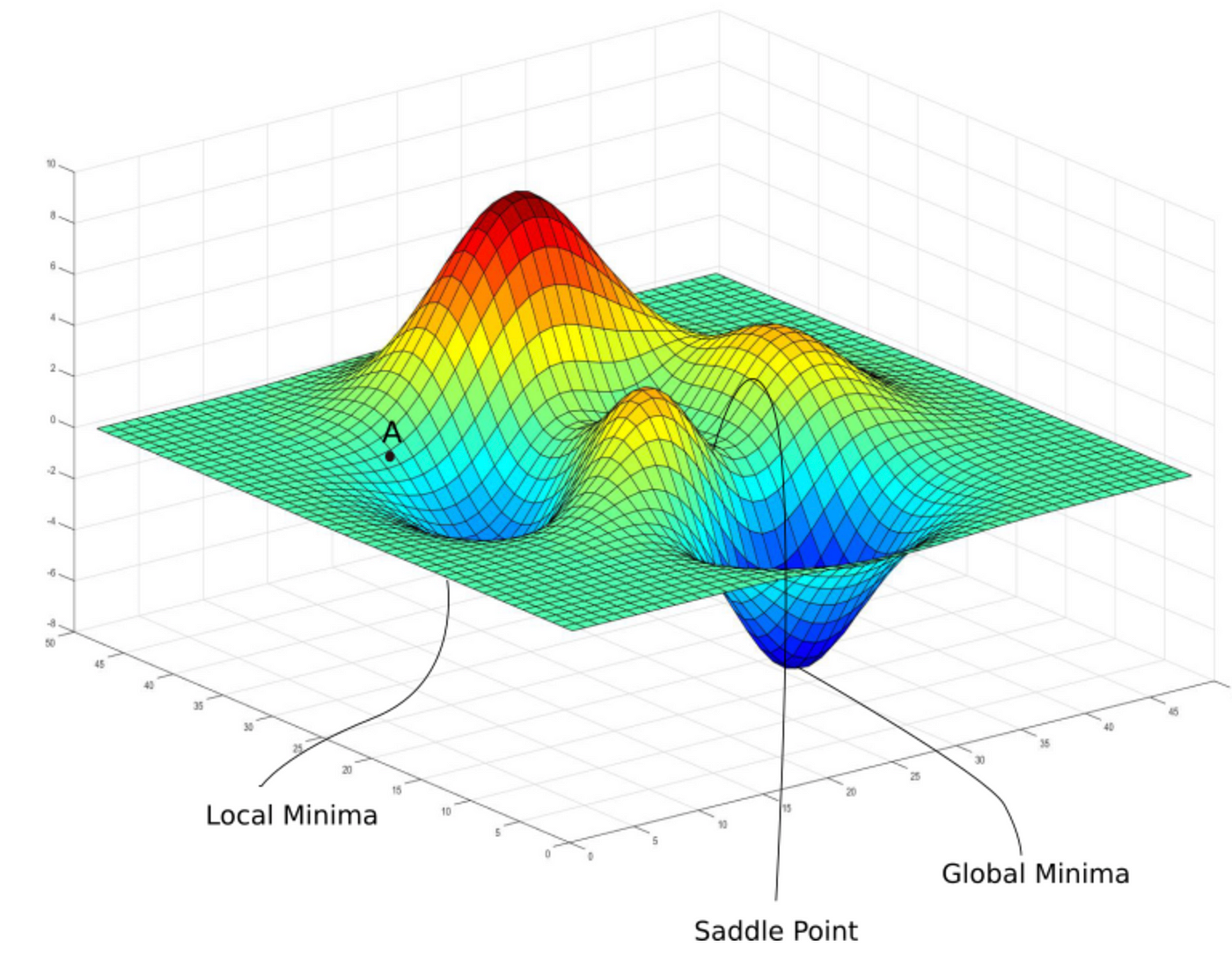
- More common in deep learning and complex machine learning models.
- There can be multiple local minima.
- Example: Functions with multiple peaks and valleys, such as .
Multiple Features
Introduction
In real-world scenarios, a single feature is often not enough to make accurate predictions. For example, if we want to predict the price of a house, using only its size (square meters) might not be sufficient. Other factors such as the number of bedrooms, location, and age of the house also play an important role.
When we have multiple features, our hypothesis function extends to:
where:
- are the input features,
- are the parameters (weights) we need to learn.
For instance, in a house price prediction model, the hypothesis function could be:
This allows our model to consider multiple factors, improving its accuracy compared to using a single feature.
Vectorization
To optimize computations, we represent our hypothesis function using matrix notation:
where:
is the matrix containing training examples
is the parameter vector
This allows efficient computation using matrix operations instead of looping over individual training examples.
Why Vectorization?
Vectorization is the process of converting operations that use loops into matrix operations. This improves computational efficiency, especially when working with large datasets. Instead of computing predictions one by one using a loop, we leverage linear algebra to perform all calculations simultaneously.
Without vectorization (using a loop):
m = len(X) # Number of training examples
h = []
for i in range(m):
prediction = theta_0 + theta_1 * X[i, 1] + theta_2 * X[i, 2] + ... + theta_n * X[i, n]
h.append(prediction)
With vectorization:
h = np.dot(X, theta) # Compute all predictions at once
This method is significantly faster because it takes advantage of optimized numerical libraries like NumPy that execute matrix operations efficiently.
Vectorized Cost Function
Similarly, our cost function for multiple features is:
Using matrices, this can be written as:
And implemented in Python as:
def compute_cost(X, y, theta):
m = len(y) # Number of training examples
error = np.dot(X, theta) - y # Compute (Xθ - y)
cost = (1 / (2 * m)) * np.dot(error.T, error) # Compute cost function
return cost
By using vectorized operations, we achieve a significant performance boost compared to using explicit loops.
Feature Scaling
When working with multiple features, the range of values across different features can vary significantly. This can negatively affect the performance of gradient descent, causing slow convergence or inefficient updates. Feature scaling is a technique used to normalize or standardize features to bring them to a similar scale, improving the efficiency of gradient descent.
Why Feature Scaling is Important
- Features with large values can dominate the cost function, leading to inefficient updates.
- Gradient descent converges faster when features are on a similar scale.
- Helps prevent numerical instability when computing gradients.
Methods of Feature Scaling
1. Min-Max Scaling (Normalization)
Brings all feature values into a fixed range, typically between 0 and 1:
- Best for cases where the distribution of data is not Gaussian.
- Sensitive to outliers, as extreme values affect the range.
2. Standardization (Z-Score Normalization)
Centers data around zero with unit variance:
where:
-
is the mean of the feature values
-
is the standard deviation
-
Works well when features follow a normal distribution.
-
Less sensitive to outliers compared to min-max scaling.
Example
Consider a dataset with two features: House Size (m²) and Number of Bedrooms.
| House Size (m²) | Bedrooms |
|---|---|
| 2100 | 3 |
| 1600 | 2 |
| 2500 | 4 |
| 1800 | 3 |
Using min-max scaling:
| House Size (scaled) | Bedrooms (scaled) |
|---|---|
| 0.714 | 0.5 |
| 0.0 | 0.0 |
| 1.0 | 1.0 |
| 0.286 | 0.5 |
Feature Scaling in Gradient Descent
After scaling, gradient descent updates will be more balanced across different features, leading to faster and more stable convergence. Feature scaling is a critical preprocessing step in machine learning models involving optimization algorithms like gradient descent.
Feature Engineering and Polynomial Regression
- Feature Engineering
- Polynomial Regression
Feature Engineering
Introduction to Feature Engineering
Feature engineering is the process of transforming raw data into meaningful features that improve the predictive power of machine learning models. It involves creating new features, modifying existing ones, and selecting the most relevant features to enhance model performance.
Why is Feature Engineering Important?
- Improves model accuracy: Well-engineered features help models learn better representations of the data.
- Reduces model complexity: Properly engineered features can make complex models simpler and more interpretable.
- Enhances generalization: Good feature selection prevents overfitting and improves performance on unseen data.
Real-World Example
Consider a house price prediction problem. Instead of using just raw data such as square footage and the number of bedrooms, we can create new features like:
- Price per square foot =
Price / Size - Age of the house =
Current Year - Year Built - Proximity to city center =
Distance in km
These engineered features often provide better insights and improve model performance compared to using raw data alone.
Feature Transformation
Feature transformation involves applying mathematical operations to existing features to make data more suitable for machine learning models.
1. Log Transformation
Used to reduce skewness and stabilize variance in highly skewed data.
Example: Income Data
Many income datasets have a right-skewed distribution where most values are low, but a few values are extremely high. Applying a log transformation makes the data more normal:
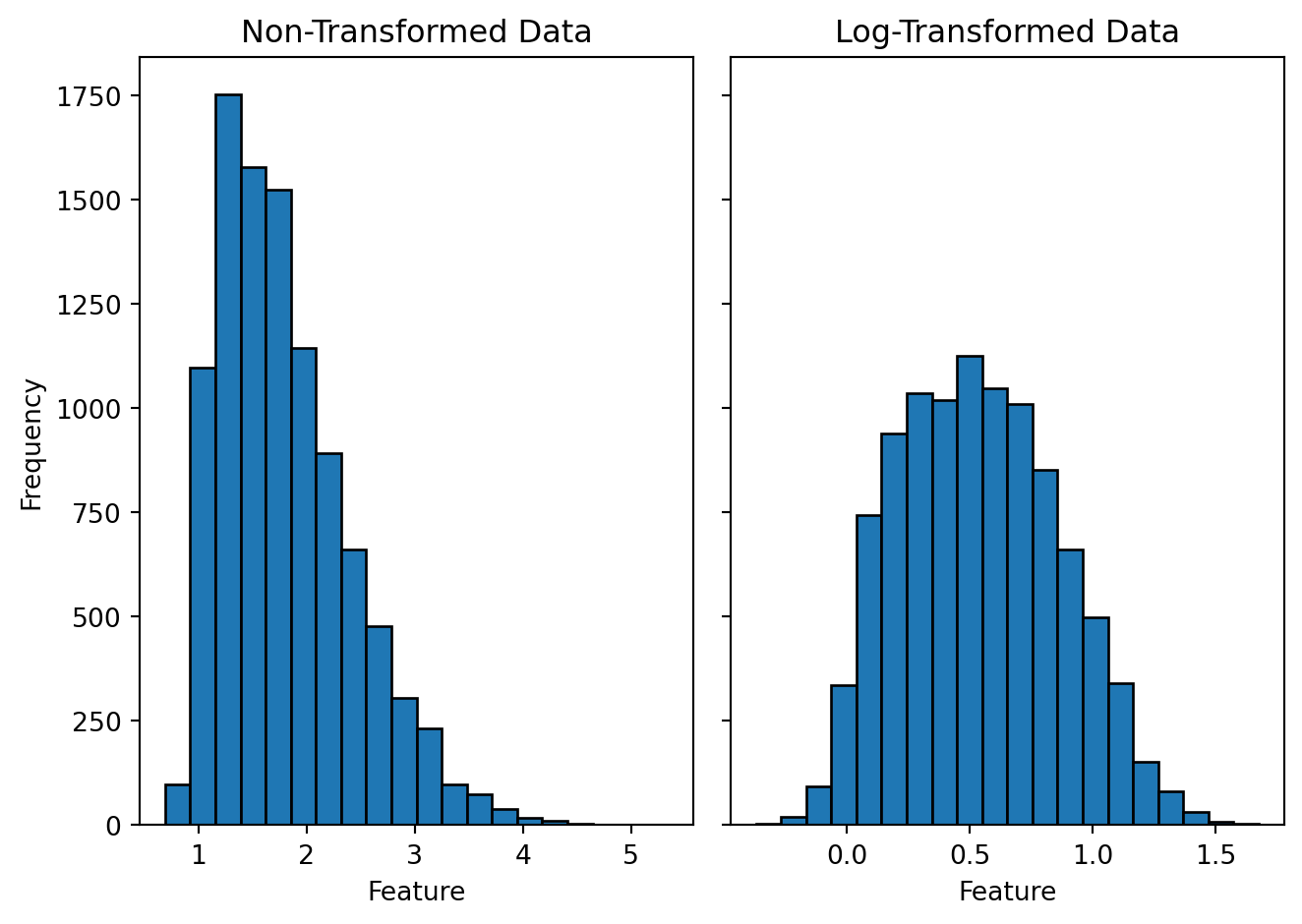
2. Polynomial Features
Adding polynomial terms (squared, cubic) to capture non-linear relationships.
Example: House Price Prediction
Instead of using Size as a single feature, we can include Size^2 and Size^3 to better fit non-linear patterns.
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
X = np.array([[1000], [1500], [2000], [2500]]) # House sizes
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)
print(X_poly)
3. Interaction Features
Creating new features based on interactions between existing ones.
Example: Combining Features
Instead of using Height and Weight separately for a health model, create a new BMI feature:
def calculate_bmi(height, weight):
return weight / (height ** 2)
height = np.array([1.65, 1.75, 1.80]) # Heights in meters
weight = np.array([65, 80, 90]) # Weights in kg
bmi = calculate_bmi(height, weight)
print(bmi)
This allows the model to understand health risks better than using height and weight separately.
Feature Selection
Feature selection involves identifying the most relevant features for a model while removing unnecessary or redundant ones. This improves model performance and reduces computational complexity.
1. Unnecessary Features
Not all features contribute equally to model performance. Some may be irrelevant or redundant, leading to overfitting and increased computational cost. Examples of unnecessary features include:
- ID columns: Unique identifiers that do not provide predictive value.
- Highly correlated features: Features that contain similar information.
- Constant or near-constant features: Features with little to no variation.
2. Correlation Analysis
Correlation analysis helps detect multicollinearity, where two or more features are highly correlated. If two features provide similar information, one of them can be removed.
Example: Finding Highly Correlated Features
import pandas as pd
import numpy as np
# Sample dataset
data = {
'Feature1': [1, 2, 3, 4, 5],
'Feature2': [2, 4, 6, 8, 10],
'Feature3': [5, 3, 6, 9, 2]
}
df = pd.DataFrame(data)
# Compute correlation matrix
correlation_matrix = df.corr()
print(correlation_matrix)
Features with a correlation coefficient close to ±1 can be considered redundant and removed.
3. Statistical Feature Selection Methods
Feature selection techniques can be used to rank the importance of different features based on statistical tests or model-based importance measures.
At this stage it is enough to learn superficially !
Common Methods:
- Chi-Square Test: Measures dependency between categorical features and the target variable.
- Mutual Information: Evaluates how much information a feature contributes.
- Recursive Feature Elimination (RFE): Iteratively removes less important features based on model performance.
- Feature Importance from Tree-Based Models: Decision trees and random forests provide feature importance scores.
Feature selection ensures that only the most valuable features are used in the final model, improving efficiency and predictive power.
Polynomial Regression
Introduction to Polynomial Regression
Polynomial Regression is an extension of Linear Regression that models non-linear relationships between input features and the target variable. While Linear Regression assumes a straight-line relationship, Polynomial Regression captures curves and more complex patterns.
Why Use Polynomial Regression?
- Handles Non-Linearity: Unlike Linear Regression, which assumes a direct relationship, Polynomial Regression models curved trends.
- Better Fit for Real-World Data: Many real-world phenomena, such as population growth, economic trends, and physics-based models, exhibit non-linear behavior.
- Feature Engineering Alternative: Instead of manually creating interaction terms, Polynomial Regression provides an automatic way to capture complex dependencies.
Example: Predicting House Prices
Consider a dataset where house prices do not increase linearly with size. Instead, they follow a non-linear trend due to factors like demand, location, and infrastructure. A Polynomial Regression model can better capture this pattern.
For instance:
- Linear Model:
- Polynomial Model:
This quadratic term helps model the curved price trend more accurately.
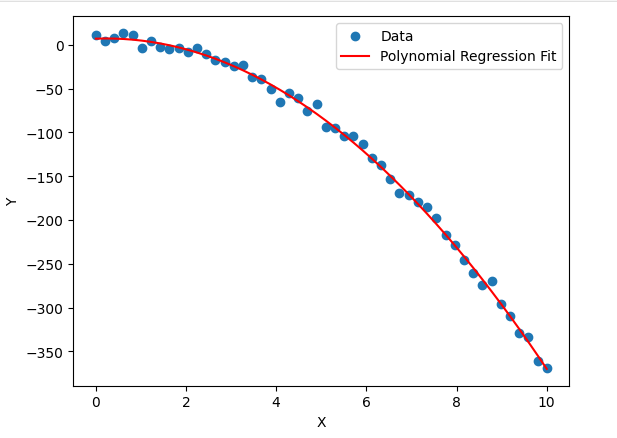
Mathematical Representation and Implementation
Polynomial regression extends linear regression by adding polynomial terms to the feature set. The hypothesis function is represented as:
where:
- is the input feature,
- are the parameters (weights),
- represents higher-degree polynomial terms.
This allows the model to capture non-linear relationships in the data.
Classification with Logistic Regression
- 1. Introduction to Classification
- 2. Logistic Regression
- 3. Cost Function for Logistic Regression
- 4. Gradient Descent for Logistic Regression
1. Introduction to Classification
Classification is a supervised learning problem where the goal is to predict discrete categories instead of continuous values. Unlike regression, which predicts numerical values, classification assigns data points to labels or classes.
Classification vs. Regression
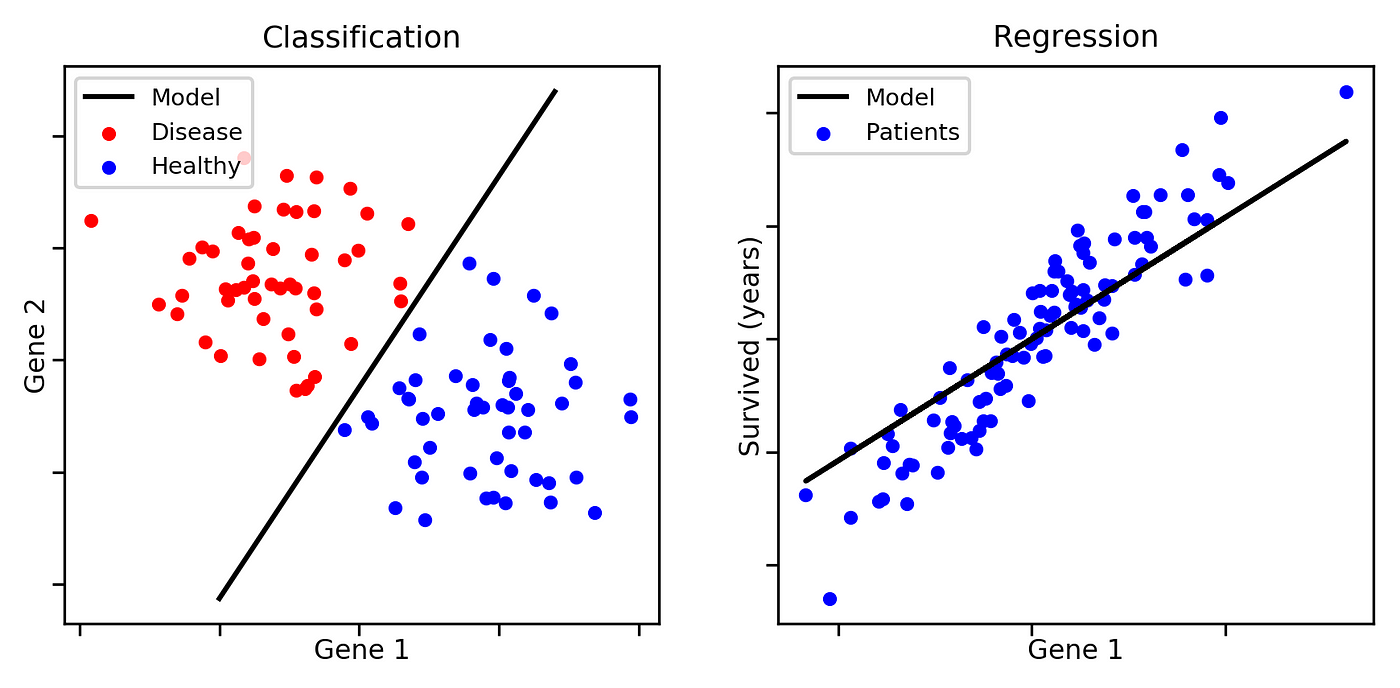
| Feature | Regression | Classification |
|---|---|---|
| Output Type | Continuous | Discrete |
| Example | Predicting house prices | Email spam detection |
| Algorithm Example | Linear Regression | Logistic Regression |
Examples of Classification Problems
- Email Spam Detection: Classify emails as "spam" or "not spam".
- Medical Diagnosis: Identify whether a patient has a disease (yes/no).
- Credit Card Fraud Detection: Determine if a transaction is fraudulent or legitimate.
- Image Recognition: Classifying images as "cat" or "dog".
Classification models can be:
- Binary Classification: Only two possible outcomes (e.g., spam or not spam).
- Multi-class Classification: More than two possible outcomes (e.g., classifying handwritten digits 0-9).
2. Logistic Regression
Introduction to Logistic Regression
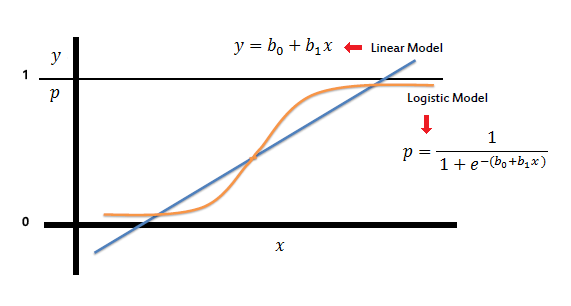
Logistic regression is a statistical model used for binary classification problems. Unlike linear regression, which predicts continuous values, logistic regression predicts probabilities that map to discrete class labels.
Linear regression might seem like a reasonable approach for classification, but it has major limitations:
- Unbounded Output: Linear regression produces outputs that can take any real value, meaning predictions could be negative or greater than 1, which makes no sense for probability-based classification.
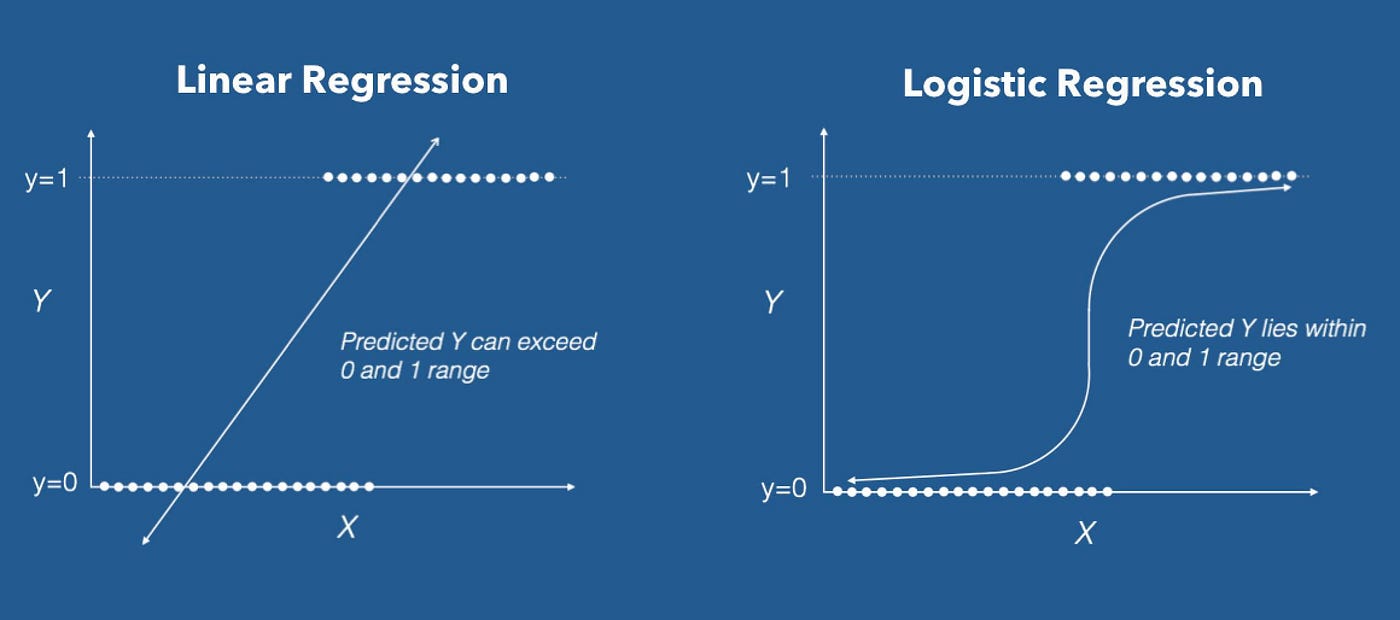
- Poor Decision Boundaries: If we use a linear function for classification, extreme values in the dataset can distort the decision boundary, leading to incorrect classifications.
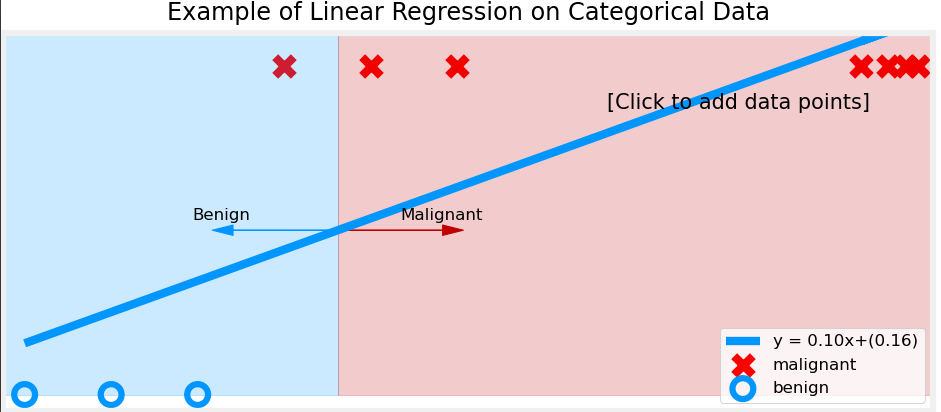
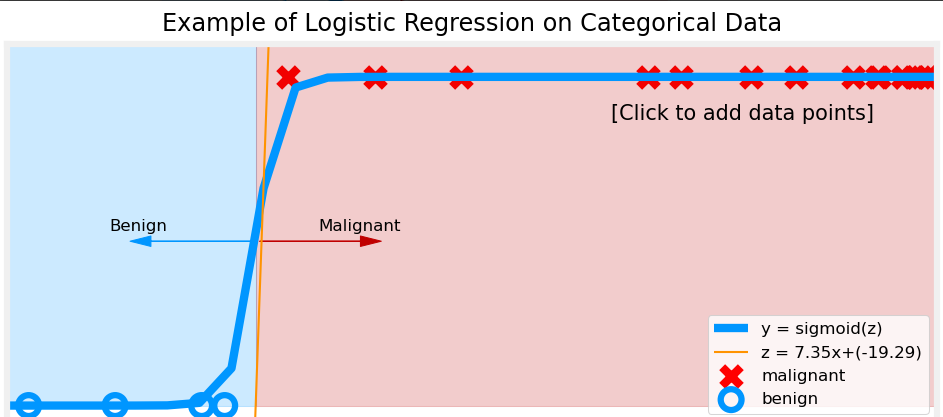
To solve these issues, we use logistic regression, which applies the sigmoid function to transform outputs into a probability range between 0 and 1.
Why Do We Need the Sigmoid Function?
The sigmoid function is a key component of logistic regression. It ensures that outputs always remain between 0 and 1, making them interpretable as probabilities.
Consider a fraud detection system that predicts whether a transaction is fraudulent (1) or legitimate (0) based on customer behavior. Suppose we use a linear model:
For some transactions, the output might be y = 7.5 or y = -3.2, which do not make sense as probability values. Instead, we use the sigmoid function to squash any real number into a valid probability range:
This function maps:
- Large positive values to probabilities close to 1 (fraudulent transaction).
- Large negative values to probabilities close to 0 (legitimate transaction).
- Values near 0 to probabilities near 0.5 (uncertain classification).
Sigmoid Function and Probability Interpretation
The output of the sigmoid function can be interpreted as:
- → The model predicts Class 1 (e.g., spam email, fraudulent transaction).
- → The model predicts Class 0 (e.g., not spam email, legitimate transaction).
For a final classification decision, we apply a threshold (typically 0.5):
This means:
- If the probability is ≥ 0.5, we classify the input as 1 (positive class).
- If the probability is < 0.5, we classify it as 0 (negative class).
Decision Boundary
The decision boundary is the surface that separates different classes in logistic regression. It is the point at which the model predicts a probability of 0.5, meaning the model is equally uncertain about the classification.
Since logistic regression produces probabilities using the sigmoid function, we define the decision boundary mathematically as:
Taking the inverse of the sigmoid function, we get:
This equation defines the decision boundary as a linear function in the feature space.
Understanding the Decision Boundary with Examples
1. Single Feature Case (1D)
If we have only one feature , the model equation is:
Solving for :
This means that when crosses this threshold, the model switches from predicting Class 0 to Class 1.
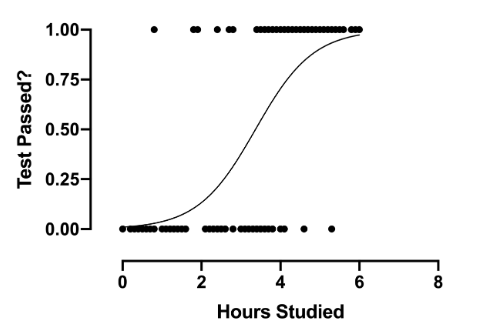
Example: Imagine predicting whether a student passes or fails based on study hours ():
- If hours → Fail (Class 0).
- If hours → Pass (Class 1).
The decision boundary in this case is simply .
2. Two Features Case (2D)
For two features and , the decision boundary equation becomes:
Rearranging:
This represents a straight line separating the two classes in a 2D plane.
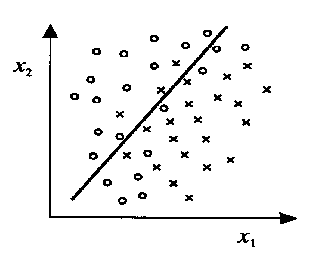
Example: Suppose we classify students as passing (1) or failing (0) based on study hours () and sleep hours ():
- The decision boundary could be:
- If is above the line, classify as pass.
- If is below the line, classify as fail.
3. Two Features Case (3D)
When we move to three features , , and , the decision boundary becomes a plane in three-dimensional space:
Rearranging for :
This equation represents a flat plane dividing the 3D space into two regions, one for Class 1 and the other for Class 0.
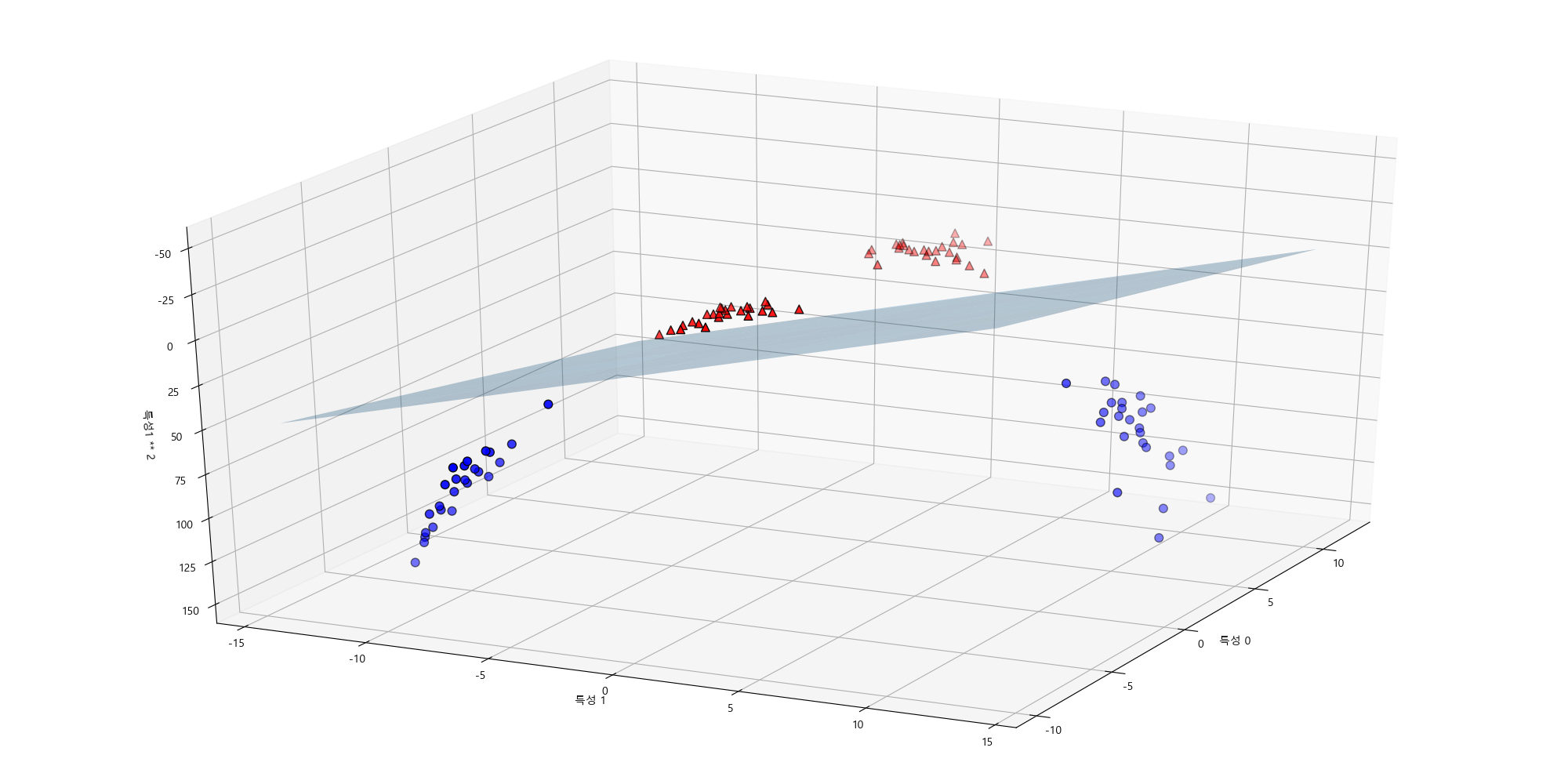
Example:
Imagine predicting whether a company will be profitable (1) or not (0) based on:
- Marketing Budget ()
- R&D Investment ()
- Number of Employees ()
The decision boundary would be a plane in 3D space, separating profitable and non-profitable companies.
In general, for n features, the decision boundary is a hyperplane in an n-dimensional space.
4. Non-Linear Decision Boundaries in Depth
So far, we have seen that logistic regression creates linear decision boundaries. However, many real-world problems have non-linear relationships. In such cases, a straight line (or plane) is not sufficient to separate classes.
To capture complex decision boundaries, we introduce polynomial features or feature transformations.
Example 1: Circular Decision Boundary
If the data requires a circular boundary, we can use quadratic terms:
This represents a circle in 2D space.
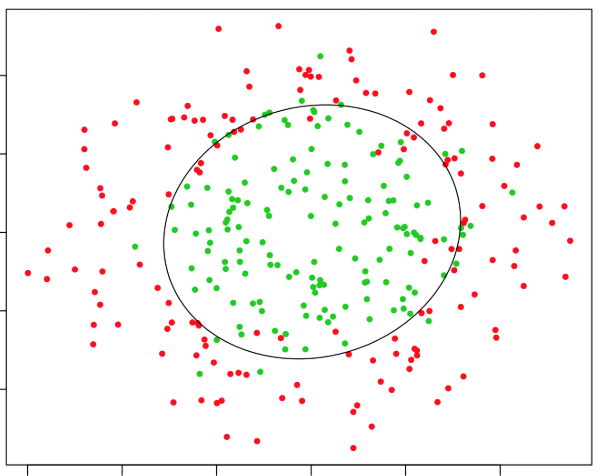
For example:
-
If and are the coordinates of points, a decision boundary like:
would classify points inside a radius-2 circle as Class 1 and outside as Class 0.
Example 2: Elliptical Decision Boundary
A more general quadratic equation:
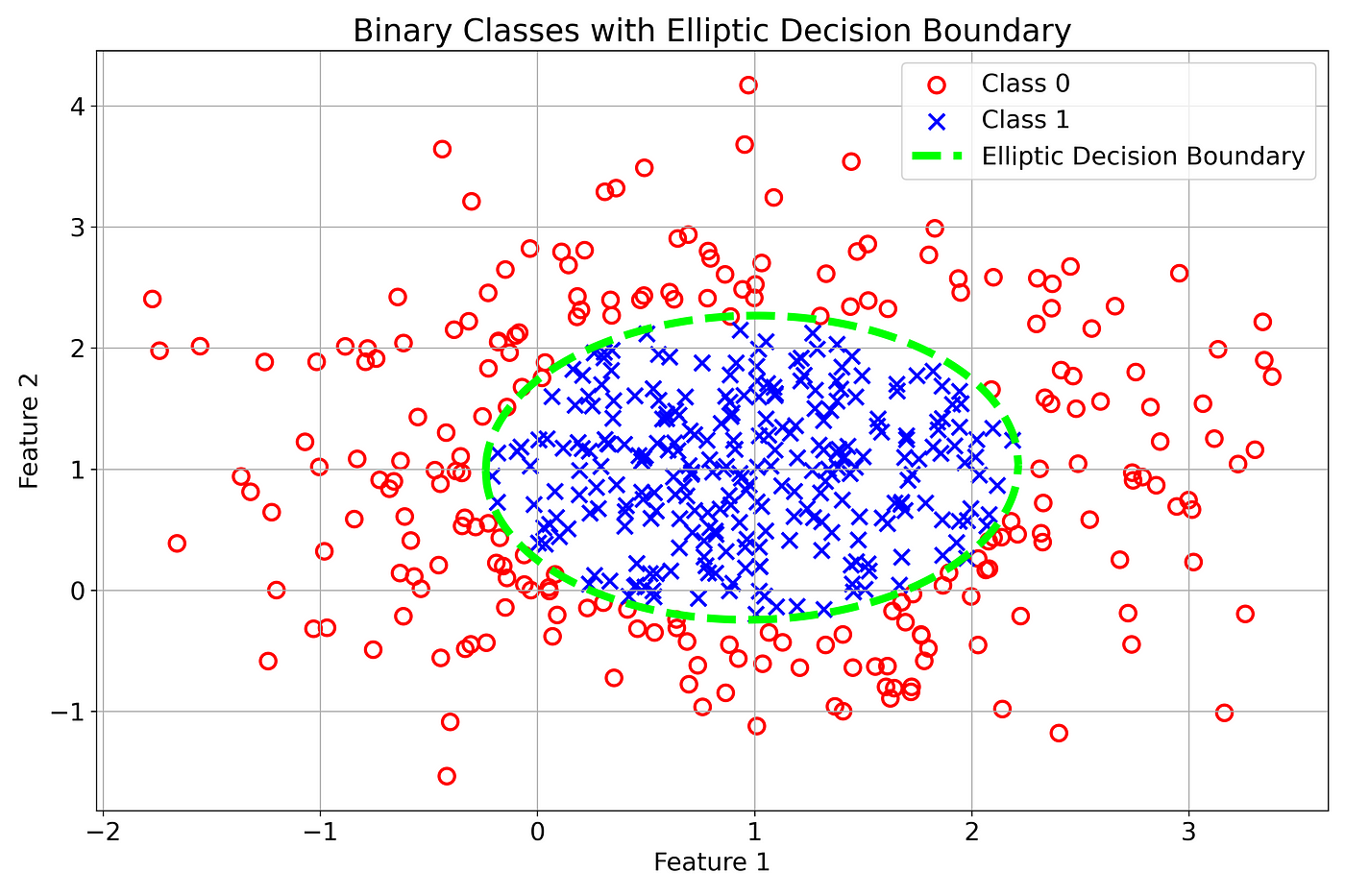
This allows for elliptical decision boundaries.
Example 3: Complex Non-Linear Boundaries
For even more complex boundaries, we can include higher-order polynomial features, such as:
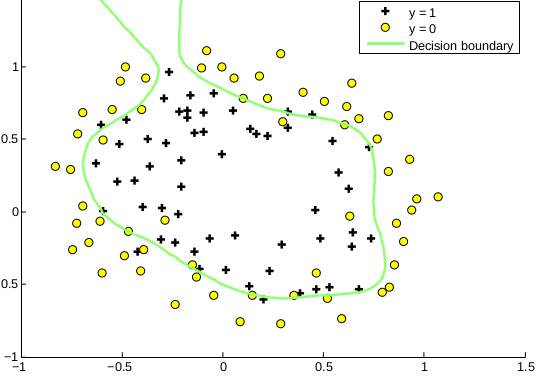
This enables twists and curves in the decision boundary, allowing logistic regression to model highly non-linear patterns.
Feature Engineering for Non-Linear Boundaries
- Instead of adding polynomial terms manually, we can transform features using basis functions (e.g., Gaussian kernels or radial basis functions).
- Feature maps can convert non-linearly separable data into a higher-dimensional space where a linear decision boundary works.
Limitations of Logistic Regression for Non-Linear Boundaries
- Feature engineering is required: Unlike neural networks or decision trees, logistic regression cannot learn complex boundaries automatically.
- Higher-degree polynomials can lead to overfitting: Too many non-linear terms make the model sensitive to noise.
Key Takeaways
- In 3D, the decision boundary is a plane, and in higher dimensions, it becomes a hyperplane.
- Non-linear decision boundaries can be created using quadratic, cubic, or transformed features.
- Feature engineering is crucial to make logistic regression work well for non-linearly separable problems.
- Too many high-order polynomial terms can cause overfitting, so regularization is needed.
3. Cost Function for Logistic Regression
1. Why Do We Need a Cost Function?
In linear regression, we use the Mean Squared Error (MSE) as the cost function:
However, this cost function does not work well for logistic regression because:
- The hypothesis function in logistic regression is non-linear due to the sigmoid function.
- Using squared errors results in a non-convex function with multiple local minima, making optimization difficult.
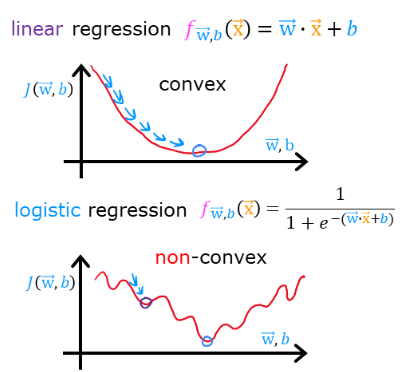
We need a different cost function that:
✅ Works well with the sigmoid function.
✅ Is convex, so gradient descent can efficiently minimize it.
2. Simplified Cost Function for Logistic Regression
Instead of using squared errors, we use a log loss function:
Where:
- is the true label (0 or 1).
- is the predicted probability from the sigmoid function.
This function ensures:
- If → The first term dominates: , which is close to 0 if (correct prediction).
- If → The second term dominates: , which is close to 0 if .
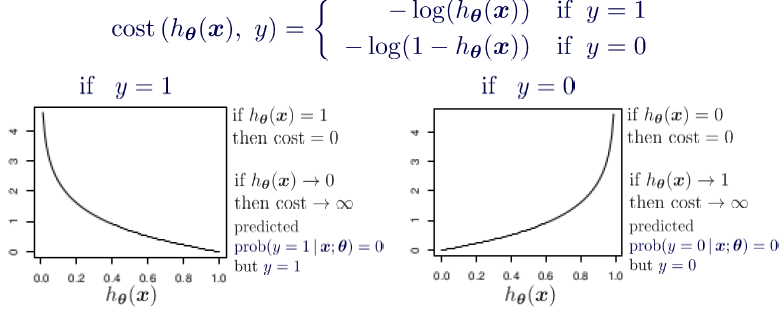
✅ Interpretation: The function penalizes incorrect predictions heavily while rewarding correct predictions.
3. Intuition Behind the Cost Function
Let’s break it down:
-
When , the cost function simplifies to:
This means:
- If (correct prediction), → No penalty.
- If (wrong prediction), → High penalty!
-
When , the cost function simplifies to:
This means:
- If (correct prediction), → No penalty.
- If (wrong prediction), → High penalty!
✅ Key Takeaway:
The function assigns very high penalties for incorrect predictions, encouraging the model to learn correct classifications.
4. Gradient Descent for Logistic Regression
1. Why Do We Need Gradient Descent?
In logistic regression, our goal is to find the best parameters that minimize the cost function:
Since there is no closed-form solution like in linear regression, we use gradient descent to iteratively update until we reach the minimum cost.
2. Gradient Descent Algorithm
Gradient descent updates the parameters using the rule:
Where:
- is the learning rate (step size).
- is the gradient (direction of steepest increase).
For logistic regression, the derivative of the cost function is:
Thus, the update rule becomes:
✅ Key Insight:
- We compute the error: .
- Multiply it by the feature .
- Average over all training examples.
- Scale by and update .
Overfitting and Regularization
- 1. The Problem of Overfitting
- 2. Addressing Overfitting
- 3. Regularized Cost Function
- 4. Regularized Linear Regression
- 5. Regularized Logistic Regression
1. The Problem of Overfitting
What is Overfitting?
Overfitting occurs when a machine learning model learns the training data too well, capturing noise and random fluctuations rather than the underlying pattern. As a result, the model performs well on training data but generalizes poorly to unseen data.
Symptoms of Overfitting
- High training accuracy but low test accuracy (poor generalization).
- Complex decision boundaries that fit training data too closely.
- Large model parameters (high magnitude weights), leading to excessive sensitivity to small changes in input data.
Example of Overfitting in Regression
Consider a polynomial regression model. If we fit a high-degree polynomial to data, the model may pass through all training points perfectly but fail to predict new data correctly.
Overfitting vs. Underfitting
| Model Complexity | Training Error | Test Error | Generalization |
|---|---|---|---|
| Underfitting (High Bias) | High | High | Poor |
| Good Fit | Low | Low | Good |
| Overfitting (High Variance) | Very Low | High | Poor |
Visualization of Overfitting
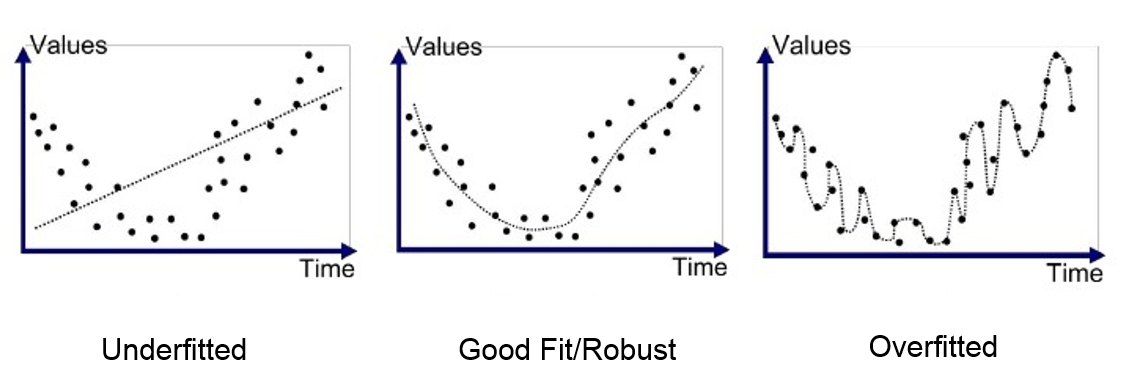
- Left (Underfitting): The model is too simple and cannot capture the trend.
- Middle (Good Fit): The model captures the pattern without overcomplicating.
- Right (Overfitting): The model follows the training data too closely, failing on new inputs.
2. Addressing Overfitting
Overfitting occurs when a model learns noise instead of the underlying pattern in the data. To address overfitting, we can apply several strategies to improve the model’s ability to generalize to unseen data.
1. Collecting More Data
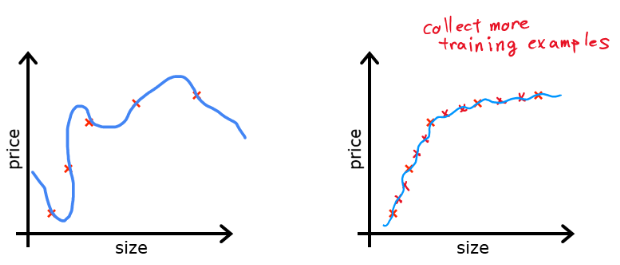
- More training data helps the model capture real patterns rather than memorizing noise.
- Especially effective for deep learning models, where small datasets tend to overfit quickly.
- Not always feasible, but can be supplemented with data augmentation techniques.
2. Feature Selection & Engineering
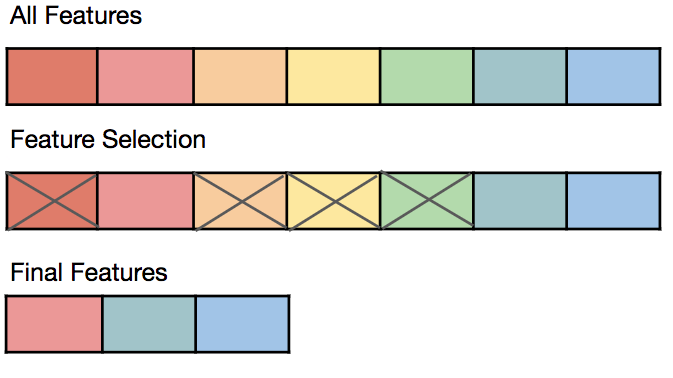
- Removing irrelevant or redundant features reduces model complexity.
- Techniques like Principal Component Analysis (PCA) help reduce dimensionality.
- Engineering new features (e.g., creating polynomial features or interaction terms) can improve generalization.
3. Cross-Validation
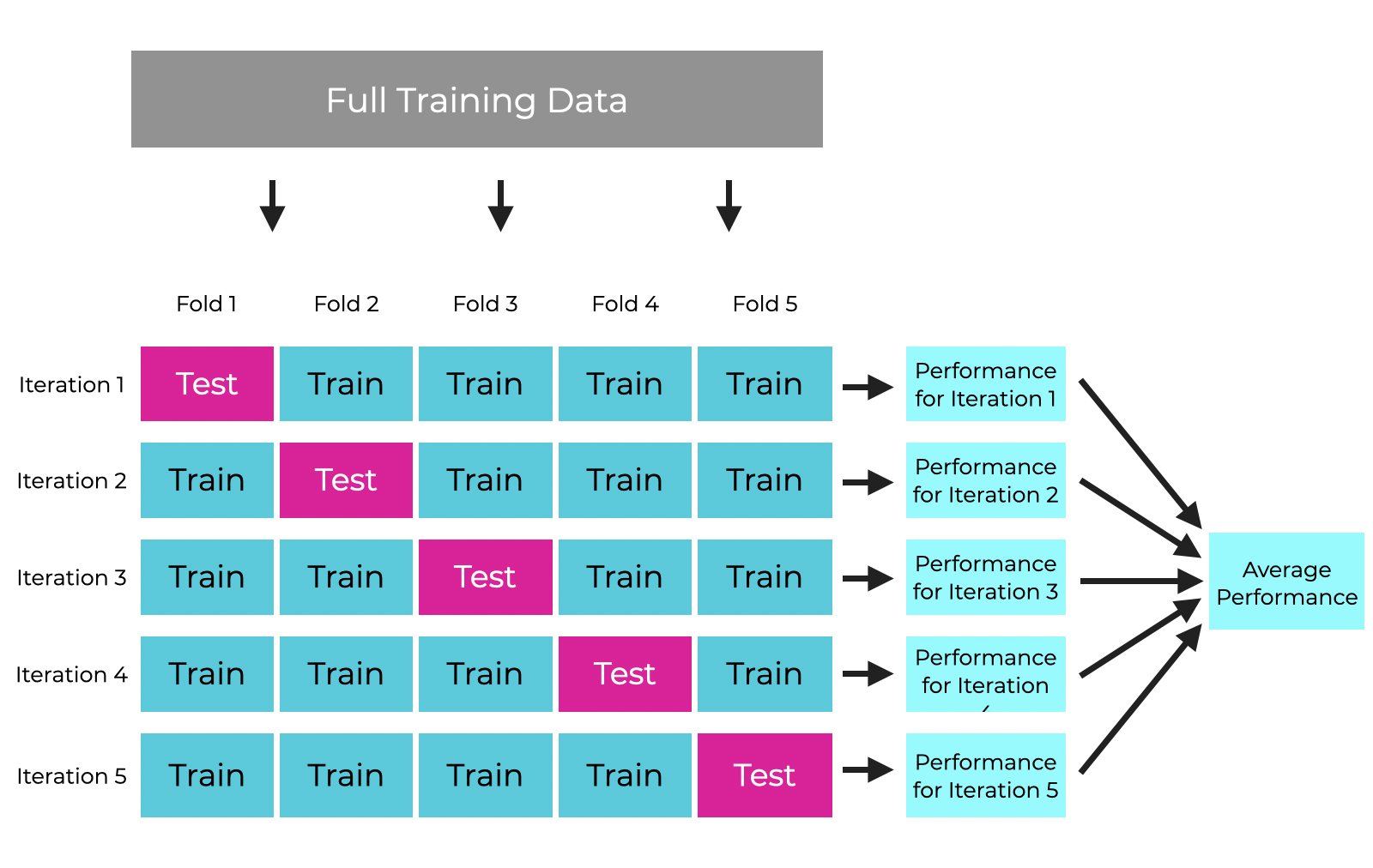
- k-fold cross-validation ensures that the model performs well on different data splits.
- Helps detect overfitting early by testing the model on multiple subsets of data.
- Leave-one-out cross-validation (LOOCV) is another approach, especially useful for small datasets.
4. Regularization as a Solution
- Regularization techniques add constraints to the model to prevent excessive complexity.
- L1 (Lasso) and L2 (Ridge) Regularization introduce penalties for large coefficients.
- We will explore regularized cost functions in the next section.
By applying these techniques, we control model complexity and improve generalization performance. In the next section, we will dive deeper into regularization and its role in the cost function.
3. Regularized Cost Function
Overfitting often occurs when a model learns excessive complexity, leading to poor generalization. One way to control this is by modifying the cost function to penalize overly complex models.
1. Why Modify the Cost Function?
The standard cost function in regression or classification only minimizes the error on training data, which can result in large coefficients (weights) that overfit the data.
By adding a regularization term, we discourage large weights, making the model simpler and reducing overfitting.
2. Adding Regularization Term
Regularization adds a penalty term to the cost function that shrinks the model parameters. The two most common types of regularization are:
L2 Regularization (Ridge Regression)
In L2 regularization, we add the sum of squared weights to the cost function:
- (regularization parameter) controls how much regularization is applied.
- Higher values force the model to reduce the magnitude of parameters, preventing overfitting.
- L2 regularization keeps all features but reduces their impact.
L1 Regularization (Lasso Regression)
In L1 regularization, we add the absolute values of weights:
- L1 regularization pushes some coefficients to zero, effectively performing feature selection.
- It results in sparser models, which are useful when many features are irrelevant.
3. Effect of Regularization on Model Complexity
Regularization controls model complexity by restricting parameter values:
- No Regularization () → The model fits the training data too closely (overfitting).
- Small → The model is still flexible but generalizes better.
- Large → The model becomes too simple (underfitting), losing important patterns.
Visualization of Regularization Effects

- Left (No Regularization): The model overfits training data.
- Middle (Moderate Regularization): The model generalizes well.
- Right (Strong Regularization): The model underfits the data.
4. Regularized Linear Regression
Linear regression without regularization can suffer from overfitting, especially when the model has too many features or when training data is limited. Regularization helps by constraining the model's parameters, preventing extreme values that lead to high variance.
1. Linear Regression Cost Function (Without Regularization)
The standard cost function for linear regression is:
where:
- is the hypothesis (predicted value),
- is the number of training examples.
This function minimizes the sum of squared errors but does not impose any restrictions on the parameter values, which can lead to overfitting.
2. Regularized Cost Function for Linear Regression
To prevent overfitting, we add an L2 regularization term (also known as Ridge Regression) to penalize large parameter values:
where:
- is the regularization parameter that controls the penalty,
- The term penalizes large values of ,
- (bias term) is not regularized.
3. Effect of Regularization in Gradient Descent
Regularization modifies the gradient descent update rule:
- The additional term shrinks the parameter values over time.
- When is too large, the model underfits (too simple).
- When is too small, the model overfits (too complex).
Effect of Regularization on Parameters
- If : Regularization is off → Overfitting risk.
- If is too high: Model is too simple → Underfitting.
- If is optimal: Good generalization → Balanced model.
4. Normal Equation with Regularization
For linear regression, we can solve for using the Normal Equation, which avoids gradient descent:
where:
- is the identity matrix (except is not regularized).
- Adding ensures is invertible, reducing multicollinearity issues.
5. Summary
✅ Regularization reduces overfitting by penalizing large weights.
✅ L2 regularization (Ridge Regression) modifies cost function by adding .
✅ Gradient Descent and Normal Equation both adjust to include regularization.
✅ Choosing is critical: too high → underfitting, too low → overfitting.
5. Regularized Logistic Regression
Logistic regression is commonly used for classification tasks, but like linear regression, it can overfit when there are too many features or limited data. Regularization helps control overfitting by penalizing large parameter values.
1. Logistic Regression Cost Function (Without Regularization)
The standard cost function for logistic regression is:
where:
- is the sigmoid function,
- is the actual class label ( or ),
- is the number of training examples.
This cost function does not include regularization, meaning the model may assign large weights to some features, leading to overfitting.
2. Regularized Cost Function for Logistic Regression
To reduce overfitting, we add an L2 regularization term, similar to regularized linear regression:
where:
- is the regularization parameter (controls penalty),
- The term discourages large parameter values,
- (bias term) is NOT regularized.
✅ Effect of Regularization
- Small → Model may overfit (complex decision boundary).
- Large → Model may underfit (too simple, missing important features).
- Optimal → Model generalizes well.
3. Effect of Regularization in Gradient Descent
Regularization modifies the gradient descent update rule:
- The regularization term shrinks the weight values over time.
- Helps avoid models that memorize training data instead of learning patterns.
4. Decision Boundary and Regularization
Regularization also affects decision boundaries:
- Without regularization (): Complex boundaries that fit noise.
- With moderate : Simpler boundaries that generalize better.
- With very high : Too simplistic boundaries that underfit.
5. Summary
✅ Regularization in logistic regression prevents overfitting by controlling parameter sizes.
✅ L2 regularization (Ridge Regression) adds to cost function.
✅ Gradient Descent is adjusted to shrink large weights.
✅ Choosing is critical for a well-generalized model.
Scikit-learn: Practical Applications
- 1. Introduction to Scikit-Learn
- 2. Linear Regression with Scikit-Learn
- 3. Multiple Linear Regression with Scikit-Learn
- 4. Polynomial Regression with Scikit-Learn
- 5. Binary Classification with Logistic Regression
- 6. Multi-Class Classification with Logistic Regression
1. Introduction to Scikit-Learn
Scikit-Learn is one of the most popular and powerful Python libraries for machine learning. It provides efficient implementations of various machine learning algorithms and tools for data preprocessing, model selection, and evaluation. It is built on top of NumPy, SciPy, and Matplotlib, making it highly compatible with the scientific computing ecosystem in Python.
Why Use Scikit-Learn?
- Easy to Use: Provides a simple and consistent API for machine learning models.
- Comprehensive: Includes a wide range of algorithms, including regression, classification, clustering, and dimensionality reduction.
- Efficient: Implements fast and optimized versions of ML algorithms.
- Integration: Works well with other libraries like Pandas, NumPy, and Matplotlib.
Loading Built-in Datasets in Scikit-Learn
Scikit-Learn provides several built-in datasets that can be used for practice and experimentation. Some common datasets include:
- Iris Dataset (
load_iris): Classification dataset for flower species. - Boston Housing Dataset (
load_boston) (Deprecated): Regression dataset for predicting house prices. - Digits Dataset (
load_digits): Handwritten digit classification. - Wine Dataset (
load_wine): Classification dataset for different types of wine. - Breast Cancer Dataset (
load_breast_cancer): Binary classification dataset for cancer diagnosis.
Example: Loading and Exploring the Iris Dataset
from sklearn.datasets import load_iris
import pandas as pd
# Load the dataset
iris = load_iris()
# Convert to DataFrame
iris_df = pd.DataFrame(iris.data, columns=iris.feature_names)
# Add target labels
iris_df['target'] = iris.target
# Display first few rows
print(iris_df.head())
Splitting Data: Train-Test Split
To evaluate a machine learning model, we need to split the data into a training set and a test set. This ensures that we can measure the model’s performance on unseen data.
Scikit-Learn provides train_test_split for this purpose:
Example: Splitting the Iris Dataset
from sklearn.model_selection import train_test_split
# Features and target variable
X = iris.data
y = iris.target
# Split into 80% training and 20% testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
print(f"Training samples: {len(X_train)}, Testing samples: {len(X_test)}")
test_size=0.2means 20% of the data is reserved for testing.random_state=42ensures reproducibility.
By following these steps, we have successfully loaded a dataset and prepared it for machine learning. In the next section, we will explore how to apply Linear Regression using Scikit-Learn.
Train-Test Split and Why It Matters
When training a machine learning model, we must evaluate its performance on unseen data to ensure it generalizes well. This is done by splitting the dataset into training and test sets.
Why Not Use 100% of Data for Training?
If we train the model using all available data, we won’t have any independent data to check how well it performs on new inputs. This leads to overfitting, where the model memorizes the training data instead of learning general patterns.
Why Not Use 90% or More for Testing?
While a large test set gives a better estimate of real-world performance, it reduces the amount of data available for training. A model trained on very little data may suffer from underfitting—it won’t have enough information to learn meaningful patterns.
What’s the Ideal Train-Test Split?
A commonly used ratio is 80% for training, 20% for testing. However, this depends on:
- Dataset Size: If data is limited, we may use a 90/10 split to keep more training data.
- Model Complexity: Simpler models may work with less training data, but deep learning models require more.
- Use Case: In critical applications (e.g., medical diagnosis), a larger test set (e.g., 30%) is preferred for reliable evaluation.
Key Takeaways
✅ 80/20 is a good starting point, but can vary based on dataset size and model needs.
✅ Too small a test set → Unreliable performance evaluation.
✅ Too large a test set → Model may not have enough training data to learn properly.
✅ Always shuffle the data before splitting to avoid biased results.
2. Linear Regression with Scikit-Learn
1. Introduction to Linear Regression
Linear regression is a fundamental supervised learning algorithm used to model the relationship between a dependent variable (target) and one or more independent variables (features). It assumes a linear relationship between input features and the output.
The mathematical form of a simple linear regression model is:
Where:
- is the predicted output.
- is the input feature.
- is the intercept (bias).
- is the coefficient (weight) of the feature.
Now, let's implement a simple linear regression model using Scikit-Learn.
2. Importing Required Libraries
First, we import necessary libraries for handling data, building the model, and evaluating its performance.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
3. Creating a Sample Dataset
We will generate a synthetic dataset to train and test our linear regression model.
# Generate random data
np.random.seed(42) # Ensures reproducibility
X = 2 * np.random.rand(100, 1) # 100 samples, single feature
y = 4 + 3 * X + np.random.randn(100, 1) # y = 4 + 3X + Gaussian noise
# Convert to a DataFrame for better visualization
df = pd.DataFrame(np.hstack((X, y)), columns=["Feature X", "Target y"])
df.head()
np.random.rand(100, 1): Generates random values between and .y = 4 + 3X + noise: Defines a linear relationship with some added noise.- We use
pd.DataFrameto display the first few samples.
4. Splitting Data into Training and Testing Sets
It is crucial to split the dataset into training and testing sets to evaluate model performance on unseen data.
# Splitting dataset into 80% training and 20% testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
print(f"Training set size: {X_train.shape[0]} samples")
print(f"Testing set size: {X_test.shape[0]} samples")
5. Training the Linear Regression Model
Now, we train a linear regression model using Scikit-Learn's LinearRegression() class.
# Create and train the model
model = LinearRegression()
model.fit(X_train, y_train)
# Print learned parameters
print(f"Intercept (theta_0): {model.intercept_[0]:.2f}")
print(f"Coefficient (theta_1): {model.coef_[0][0]:.2f}")
fit(X_train, y_train): Trains the model by finding the best-fitting line.model.intercept_: The learned bias term.model.coef_: The learned weight for the feature.
6. Making Predictions
After training, we make predictions on the test set.
# Predict on test data
y_pred = model.predict(X_test)
# Compare actual vs predicted values
comparison_df = pd.DataFrame({"Actual": y_test.flatten(), "Predicted": y_pred.flatten()})
comparison_df.head()
model.predict(X_test): Generates predictions.- The DataFrame compares actual vs. predicted values.
7. Evaluating the Model
We use Mean Squared Error (MSE) and R² Score to evaluate model performance.
# Calculate Mean Squared Error (MSE)
mse = mean_squared_error(y_test, y_pred)
# Calculate R-squared score
r2 = r2_score(y_test, y_pred)
print(f"Mean Squared Error: {mse:.2f}")
print(f"R-squared Score: {r2:.2f}")
- MSE: Measures average squared differences between actual and predicted values (lower is better).
- R² Score: Measures how well the model explains the variance in the data (closer to 1 is better).
8. Visualizing the Results
Finally, let's plot the data and the regression line.
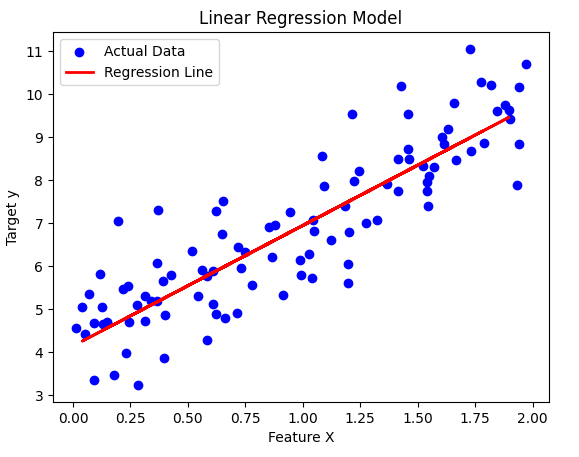
plt.scatter(X, y, color="blue", label="Actual Data")
plt.plot(X_test, y_pred, color="red", linewidth=2, label="Regression Line")
plt.xlabel("Feature X")
plt.ylabel("Target y")
plt.title("Linear Regression Model")
plt.legend()
plt.show()
This plot shows:
- Blue points → Actual test data
- Red line → Best-fit regression line
3. Multiple Linear Regression with Scikit-Learn
What is Multiple Linear Regression?
Multiple Linear Regression is an extension of simple linear regression where we predict a dependent variable () using multiple independent variables (). The general form of the equation is:
Where:
- = predicted output
- = independent variables (features)
- = intercept
- = coefficients (weights)
In this section, we will:
- Generate a synthetic dataset for a multiple linear regression model.
- Train a model using Scikit-Learn.
- Visualize the relationship in a 3D plot.
Step 1: Generate a Synthetic Dataset
First, let's create a dataset with two independent variables ( and ) and one dependent variable (). We'll add some noise to make it more realistic.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# Set seed for reproducibility
np.random.seed(42)
# Generate random data for x1 and x2
x1 = np.random.uniform(0, 10, 100)
x2 = np.random.uniform(0, 10, 100)
# Define the true equation y = 3 + 2*x1 + 1.5*x2 + noise
y = 3 + 2*x1 + 1.5*x2 + np.random.normal(0, 2, 100)
# Reshape x1 and x2 for model training
X = np.column_stack((x1, x2))
Step 2: Train the Model
Now, we split the dataset into training and test sets and train a multiple linear regression model.
# Split data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Create and train the model
model = LinearRegression()
model.fit(X_train, y_train)
# Get model parameters
theta0 = model.intercept_
theta1, theta2 = model.coef_
print(f"Model equation: y = {theta0:.2f} + {theta1:.2f}*x1 + {theta2:.2f}*x2")
Step 3: Visualize the Regression Plane
Since we have two independent variables ( and ), we can plot the regression plane in 3D space.
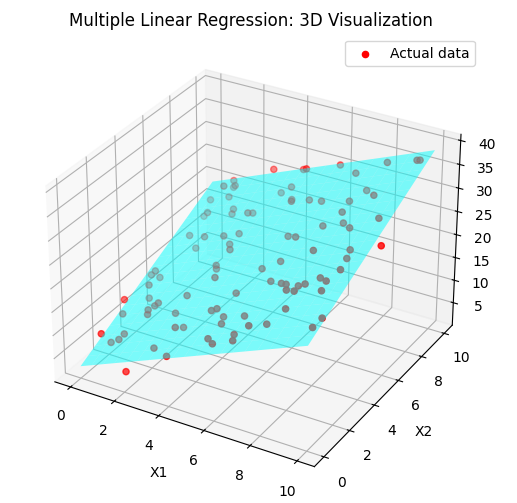
# Generate grid for x1 and x2
x1_range = np.linspace(0, 10, 20)
x2_range = np.linspace(0, 10, 20)
x1_grid, x2_grid = np.meshgrid(x1_range, x2_range)
# Compute predicted y values
y_pred_grid = theta0 + theta1 * x1_grid + theta2 * x2_grid
# Create 3D plot
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111, projection='3d')
# Scatter plot of real data
ax.scatter(x1, x2, y, color='red', label='Actual data')
# Regression plane
ax.plot_surface(x1_grid, x2_grid, y_pred_grid, alpha=0.5, color='cyan')
# Labels
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.set_zlabel('Y')
ax.set_title('Multiple Linear Regression: 3D Visualization')
plt.legend()
plt.show()
Key Takeaways
- We generated a dataset with two independent variables and one dependent variable.
- We trained a Multiple Linear Regression model using Scikit-Learn.
- We visualized the regression plane in 3D, showing how and influence .
4. Polynomial Regression with Scikit-Learn
Polynomial Regression is an extension of Linear Regression, where we introduce polynomial terms to capture non-linear relationships in the data.
1. What is Polynomial Regression?
Linear regression models relationships using a straight line:
However, if the data follows a non-linear pattern, a straight line won't fit well. Instead, we can introduce polynomial terms:
This allows the model to capture curvature in the data.
2. Generating Non-Linear Data
First, let's create a synthetic dataset with a non-linear relationship.
import numpy as np
import matplotlib.pyplot as plt
# Generate random x values between -3 and 3
np.random.seed(42)
X = np.linspace(-3, 3, 100).reshape(-1, 1)
# Generate a non-linear function with some noise
y = 0.5 * X**3 - X**2 + 2 + np.random.randn(100, 1) * 2
# Scatter plot of the data
plt.scatter(X, y, color='blue', alpha=0.5, label="True Data")
plt.xlabel("X")
plt.ylabel("y")
plt.title("Generated Non-Linear Data")
plt.legend()
plt.show()
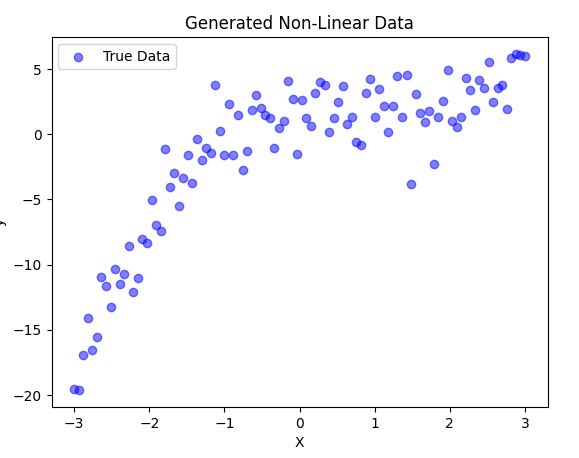
- We create 100 random points between -3 and 3.
- The function we generate follows a cubic equation:
- with added noise.
- We visualize the data using a scatter plot.
3. Applying Polynomial Features
To transform our linear features into polynomial features, we use PolynomialFeatures from sklearn.preprocessing.
from sklearn.preprocessing import PolynomialFeatures
# Transform X into polynomial features (degree=3)
poly = PolynomialFeatures(degree=3)
X_poly = poly.fit_transform(X)
print(f"Original X shape: {X.shape}")
print(f"Transformed X shape: {X_poly.shape}")
print(f"First 5 rows of X_poly:\n{X_poly[:5]}")
- We use
PolynomialFeatures(degree=3)to add polynomial terms up to . - This converts each value into a feature vector .
- We print the new shape and first few transformed rows.
4. Training a Polynomial Regression Model
Now, we train a Linear Regression model using these polynomial features.
from sklearn.linear_model import LinearRegression
# Train polynomial regression model
model = LinearRegression()
model.fit(X_poly, y)
# Predictions
y_pred = model.predict(X_poly)
5. Visualizing the Results
Let's plot the polynomial regression model against the actual data.
plt.scatter(X, y, color='blue', alpha=0.5, label="True Data")
plt.plot(X, y_pred, color='red', linewidth=2, label="Polynomial Regression Fit")
plt.xlabel("X")
plt.ylabel("y")
plt.title("Polynomial Regression Model")
plt.legend()
plt.show()
6. Comparing with Linear Regression
Now, let's compare Polynomial Regression with a simple Linear Regression model.
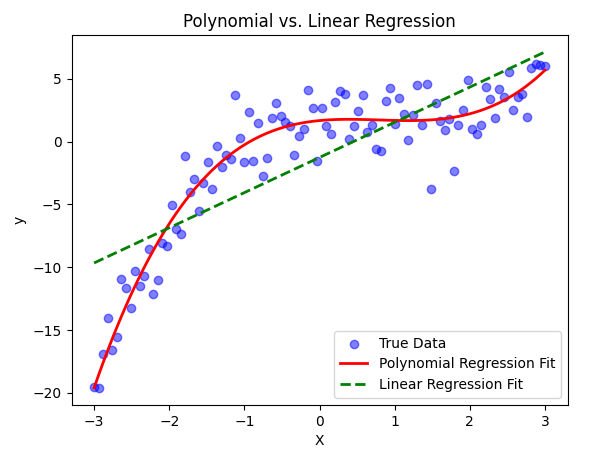
# Train a simple Linear Regression model
linear_model = LinearRegression()
linear_model.fit(X, y)
y_linear_pred = linear_model.predict(X)
# Plot both models
plt.scatter(X, y, color='blue', alpha=0.5, label="True Data")
plt.plot(X, y_pred, color='red', linewidth=2, label="Polynomial Regression Fit")
plt.plot(X, y_linear_pred, color='green', linestyle="dashed", linewidth=2, label="Linear Regression Fit")
plt.xlabel("X")
plt.ylabel("y")
plt.title("Polynomial vs. Linear Regression")
plt.legend()
plt.show()
5. Binary Classification with Logistic Regression
Logistic Regression is a fundamental algorithm used for binary classification problems. It estimates the probability that a given input belongs to a particular class using the sigmoid function.
1. What is Logistic Regression?
Unlike Linear Regression, which predicts continuous values, Logistic Regression predicts probabilities and then maps them to class labels (0 or 1). The model is defined as:
Where:
- represents the model parameters (weights and bias).
- represents the input features.
- The output is a probability between 0 and 1.
2. Generating a Synthetic Dataset (Spam Detection Example)
We'll create a synthetic dataset where emails are classified as spam (1) or not spam (0) based on two features:
- Number of suspicious words
- Email length
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# Generating synthetic data
np.random.seed(42)
num_samples = 200
# Feature 1: Number of suspicious words (randomly chosen values)
suspicious_words = np.random.randint(0, 20, num_samples)
# Feature 2: Email length (short emails tend to be spammy)
email_length = np.random.randint(20, 300, num_samples)
# Labels: Spam (1) or Not Spam (0)
labels = (suspicious_words + email_length / 50 > 10).astype(int)
# Creating feature matrix
X = np.column_stack((suspicious_words, email_length))
y = labels
# Splitting into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
3. Training the Logistic Regression Model
Now, we train a Logistic Regression model on our dataset.
# Training the model
model = LogisticRegression()
model.fit(X_train, y_train)
# Making predictions
y_pred = model.predict(X_test)
# Evaluating the model
accuracy = accuracy_score(y_test, y_pred)
print(f"Model Accuracy: {accuracy:.2f}")
4. Visualizing Decision Boundary
The decision boundary helps us see how the model separates spam from non-spam emails. We plot the boundary in 2D.
# Function to plot decision boundary
def plot_decision_boundary(model, X, y):
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 10, X[:, 1].max() + 10
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.coolwarm)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap=plt.cm.coolwarm)
plt.xlabel("Suspicious Words Count")
plt.ylabel("Email Length")
plt.title("Logistic Regression Decision Boundary")
plt.show()
# Plotting the decision boundary
plot_decision_boundary(model, X, y)
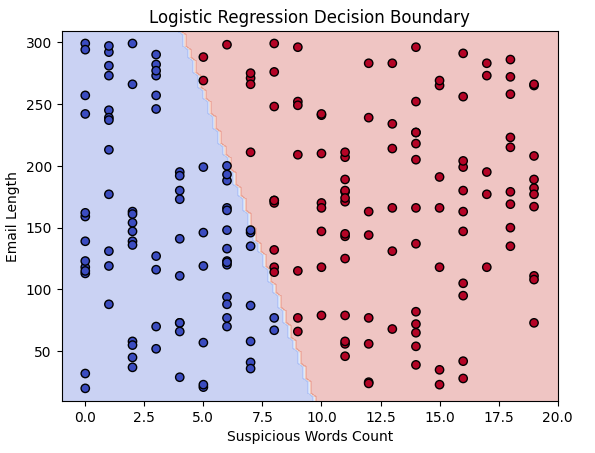
This plot shows how the model separates spam and non-spam emails using our two features.
Key Takeaways
- Logistic Regression is used for binary classification.
- It estimates probabilities using the sigmoid function.
- We generated a synthetic dataset mimicking spam detection.
- We trained and evaluated a Logistic Regression model.
- Decision boundaries help visualize how the model classifies data.
6. Multi-Class Classification with Logistic Regression
In this section, we will implement a Multi-Class Classification model using Logistic Regression. Instead of a binary classification problem, we will classify data points into three distinct categories.
This project predicts a student's success level based on study hours and past grades using Logistic Regression.
We classify students into three categories:
- Fail (0)
- Pass (1)
- High Pass (2)
Step 1: Import Libraries
We start by importing necessary libraries for:
- Data generation
- Visualization
- Model training
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import ConfusionMatrixDisplay, classification_report
Step 2: Generate Synthetic Data
We create artificial student data using make_classification.
Each student has:
- Past Grades (0-100)
- Study Hours (non-negative)
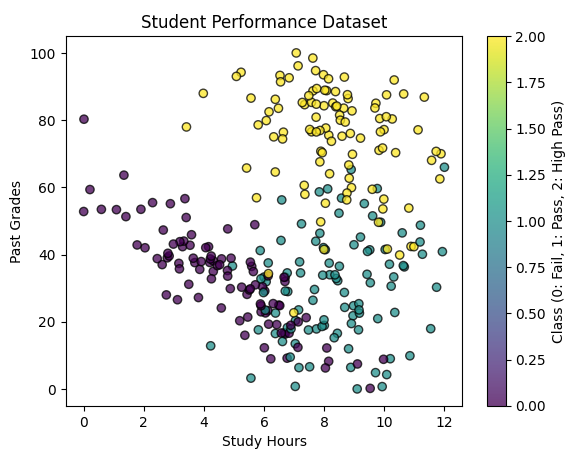
We set random_state = 457897 to ensure reproducibility.
# Generate a classification dataset
X, y = make_classification(n_samples=300,
n_features=2,
n_classes=3,
n_clusters_per_class=1,
n_informative=2,
n_redundant=0,
random_state=457897) # Ensures consistent results
# Normalize Study Hours to be non-negative & scale Past Grades (0-100)
X[:, 0] = X[:, 0] * 12
X[:, 1] = X[:, 1] * 100
# Scatter plot of generated data
plt.figure(figsize=(7, 5))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolors='k', alpha=0.75)
plt.xlabel("Study Hours")
plt.ylabel("Past Grades")
plt.title("Student Performance Dataset")
plt.colorbar(label="Class (0: Fail, 1: Pass, 2: High Pass)")
plt.show()
Step 3: Split the Data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=457897, stratify=y)
# Standardizing features for better model performance
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
Step 4: Train Logistic Regression Model
from sklearn.multiclass import OneVsRestClassifier
# Define and train the model
model = OneVsRestClassifier(LogisticRegression(solver='lbfgs'))
model.fit(X_train, y_train)
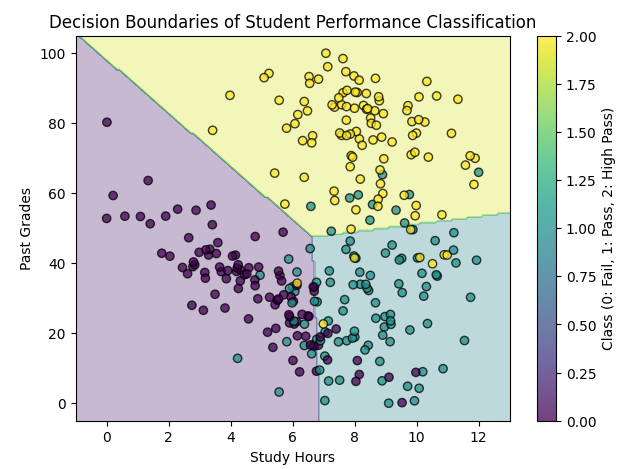
Step 5: Visualizing Decision Boundaries
# Define a mesh grid for visualization
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 5, X[:, 1].max() + 5
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 200),
np.linspace(y_min, y_max, 200))
# Predict on the mesh grid
Z = model.predict(scaler.transform(np.c_[xx.ravel(), yy.ravel()]))
Z = Z.reshape(xx.shape)
# Plot decision boundary
plt.figure(figsize=(7, 5))
plt.contourf(xx, yy, Z, alpha=0.3, cmap="viridis")
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="viridis", edgecolors='k', alpha=0.75)
plt.xlabel("Study Hours")
plt.ylabel("Past Grades")
plt.title("Decision Boundaries of Student Performance Classification")
plt.colorbar(label="Class (0: Fail, 1: Pass, 2: High Pass)")
plt.show()
Neural Networks: Intuition and Model
- Understanding Neural Networks
- Biological Inspiration: The Brain and Synapses
- Importance of Layers in Neural Networks
- Face Recognition Example: Layer-by-Layer Processing
- Mathematical Representation of a Neural Network
Understanding Neural Networks
Neural networks are a fundamental concept in deep learning, inspired by the way the human brain processes information. They consist of layers of artificial neurons that transform input data into meaningful outputs. At the core of a neural network is a simple mathematical operation: each neuron receives inputs, applies a weighted sum, adds a bias term, and passes the result through an activation function. This process allows the network to learn patterns and make predictions.
Biological Inspiration: The Brain and Synapses
Artificial neural networks (ANNs) are designed based on the biological structure of the human brain. The brain consists of billions of neurons, interconnected through structures called synapses. Neurons communicate with each other by transmitting electrical and chemical signals, which play a critical role in learning, memory, and decision-making processes.
Structure of a Biological Neuron
Each biological neuron consists of several key components:
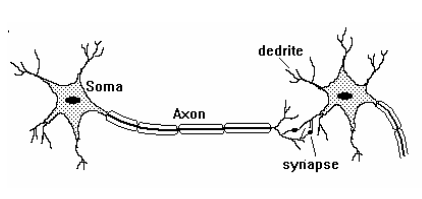
- Dendrites: Receive input signals from other neurons.
- Cell Body (Soma): Processes the received signals and determines whether the neuron should be activated.
- Axon: Transmits the output signal to other neurons.
- Synapses: Junctions between neurons where chemical neurotransmitters facilitate communication.
Artificial Neural Networks vs. Biological Networks
In artificial neural networks:
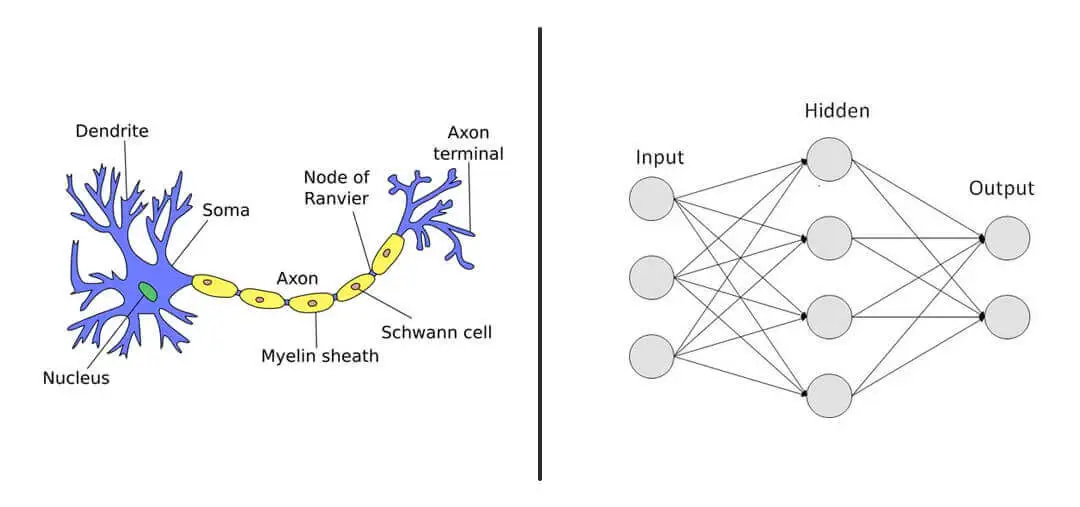
- Neurons function as computational units.
- Weights correspond to synaptic strengths, determining how influential an input is.
- Bias terms help shift the activation threshold.
- Activation functions mimic the way biological neurons fire only when certain thresholds are exceeded.
Importance of Layers in Neural Networks
Neural networks are composed of multiple layers, each responsible for extracting and processing features from input data. The more layers a network has, the deeper it becomes, allowing it to learn complex hierarchical patterns.
Example: Predicting a T-shirt's Top-Seller Status
Consider an online clothing store that wants to predict whether a new T-shirt will become a top-seller. Several factors influence this outcome, which serve as inputs to our neural network:
- Price ()
- Shipping Cost ()
- Marketing ()
- Material ()
These inputs are fed into the first layer of the network, which extracts meaningful features. A possible hidden layer structure could be:
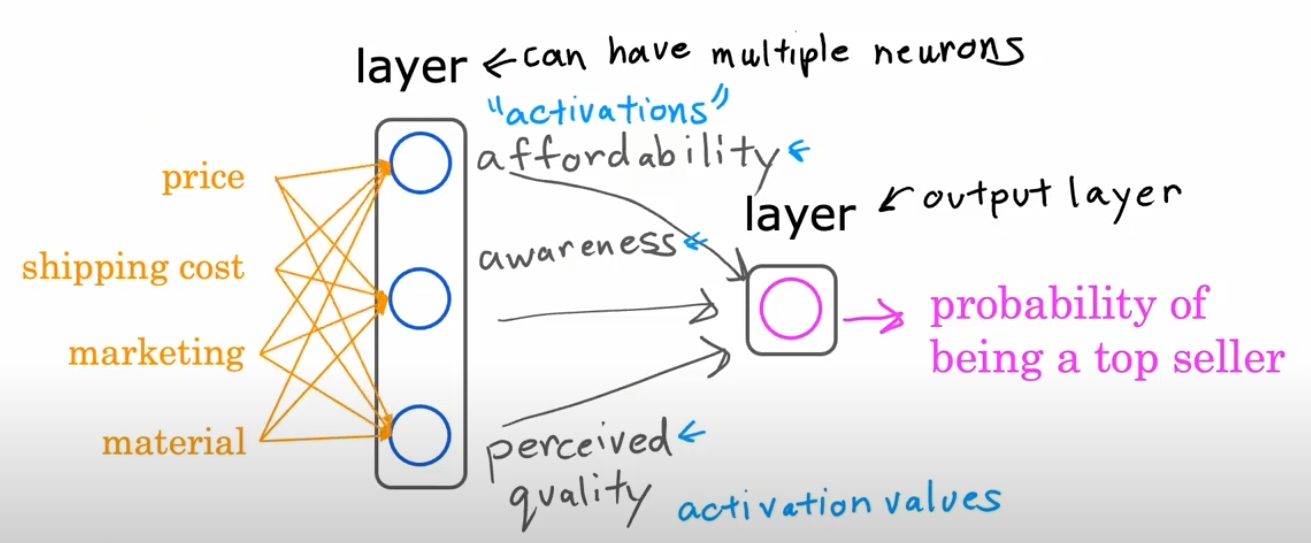
- Hidden Layer 1: Contains a few activations functions like: affordability , awareness, perceived quality.
- Output Layer: Aggregates information from the previous layers to make a final prediction.
The output layer applies a sigmoid activation function:
where is a weighted sum of the previous layer’s outputs. If , we classify the T-shirt as a top-seller; otherwise, it is not.
Face Recognition Example: Layer-by-Layer Processing
Face recognition is a real-world example where neural networks excel. Let's consider a deep neural network designed for face recognition, breaking down the processing step by step:
- Input Layer: An image of a face is converted into pixel values (e.g., a 100x100 grayscale image would be represented as a vector of 10,000 pixel values).
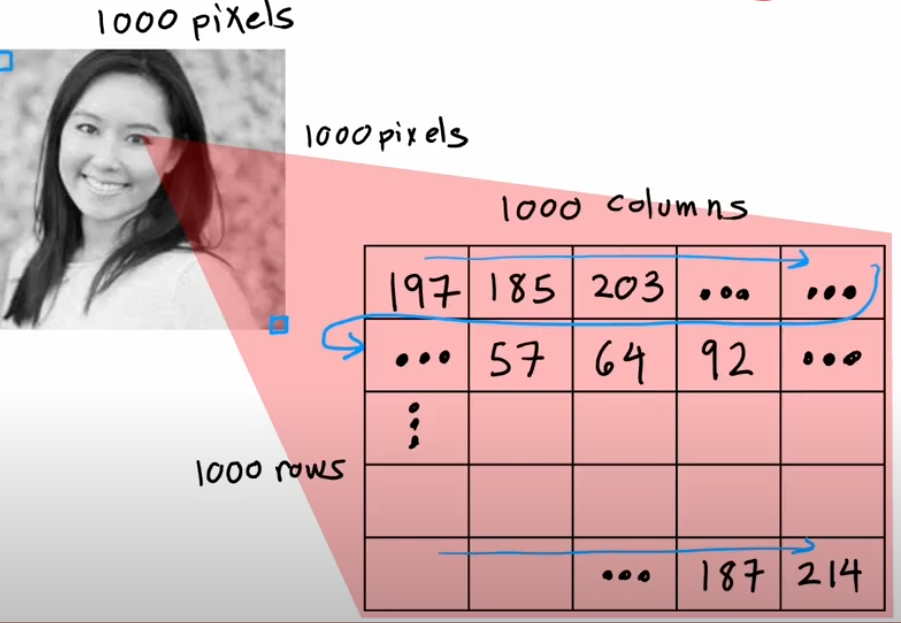
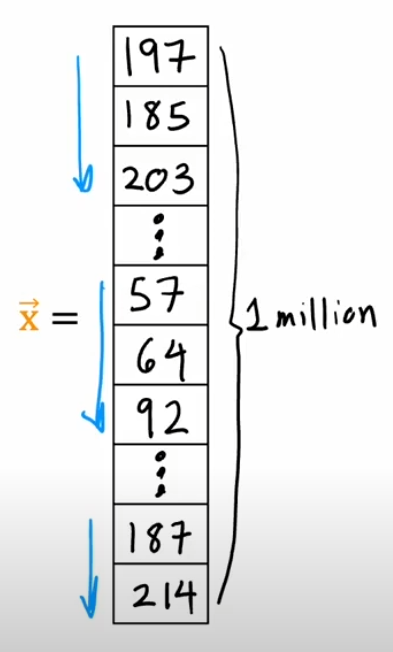
- First Hidden Layer: Detects basic edges and corners in the image by applying simple filters.
- Second Hidden Layer: Identifies facial features like eyes, noses, and mouths by combining edge and corner information.
- Third Hidden Layer: Recognizes entire facial structures and relationships between features.
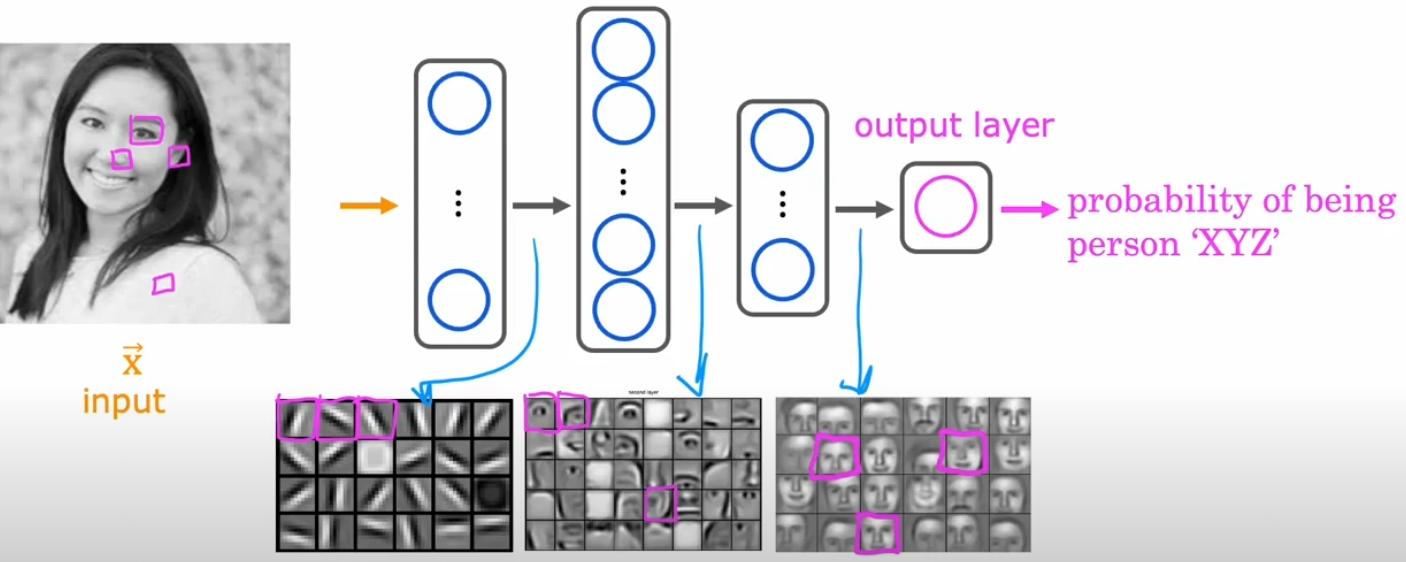
- Output Layer: Determines whether the face matches a known identity by producing a probability score.
Mathematical Representation of a Neural Network
To efficiently compute activations in a neural network, we use matrix notation. The general formula for forward propagation is:
where:
- is the activation from the previous layer,
- is the weight matrix of the current layer,
- is the bias vector,
- is the linear combination of inputs before applying the activation function.
The activation function is applied as:
where is typically a sigmoid, ReLU, or softmax function.
Example Calculation
Suppose we have a single-layer neural network with three inputs and one neuron. We define the inputs as:
The corresponding weight matrix and bias term are given by:
The weighted sum (Z) is calculated as:
Applying the sigmoid activation function:
Since the output is above 0.5, we classify this case as positive.
Two Hidden Layer Neural Network Calculation
Now, let's consider a neural network with two hidden layers.
Network Structure
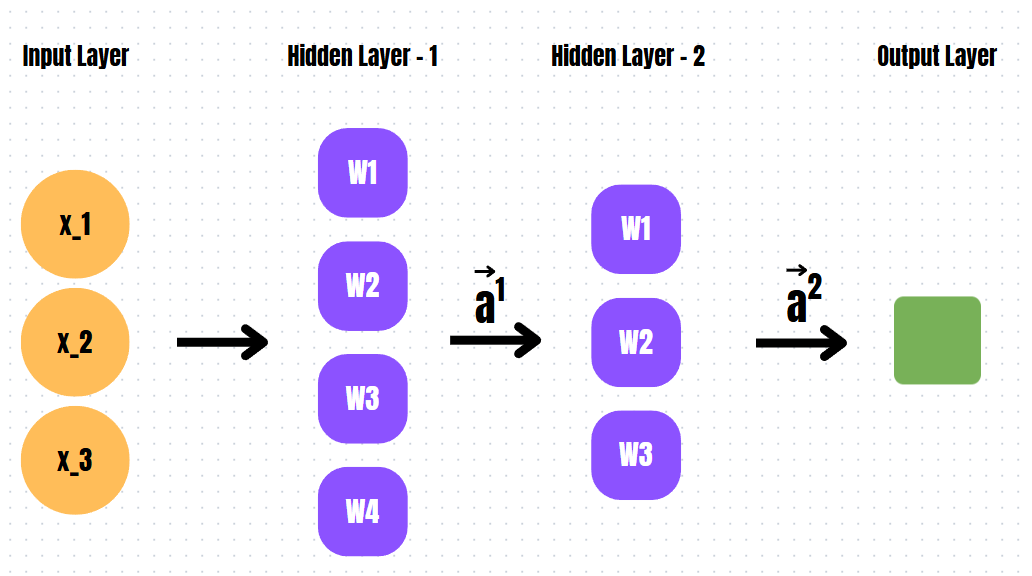
- Input Layer: 3 input values
- First Hidden Layer: 4 neurons
- Second Hidden Layer: 3 neurons
- Output Layer: 1 neuron
First Hidden Layer Calculation
Given input vector:
Weight matrix for the first hidden layer:
Bias vector:
Computing the weighted sum:
Applying the sigmoid activation function:
Second Hidden Layer Calculation
Weight matrix:
Bias vector:
Computing the weighted sum:
Applying the sigmoid activation function:
Output Layer Calculation
Weight matrix:
Bias:
Computing the final weighted sum:
Applying the sigmoid activation function:
If , the output is classified as positive.
Conclusion
- The first hidden layer extracts basic features.
- The second hidden layer learns more abstract representations.
- The output layer makes the final classification decision.
This demonstrates how a multi-layer neural network processes information in a hierarchical manner.
Handwritten Digit Recognition Using Two Layers
A classic application of neural networks is handwritten digit recognition. Let's consider recognizing the digit '1' from an 8x8 pixel grid using a simple neural network with two layers.
First Layer: Feature Extraction
- The 8x8 image is flattened into a 64-dimensional input vector.
- This vector is processed by neurons in the first hidden layer.
- The neurons identify edges, curves, and simple shapes using learned weights.
- Mathematically, the output of the first layer can be represented as:
Second Layer: Pattern Recognition
- The first layer's output is passed to a second hidden layer.
- This layer detects digit-specific features, such as the vertical stroke characteristic of '1'.
- The transformation at this stage follows:
Output Layer: Classification
- The final layer has 10 neurons, each representing a digit from 0 to 9.
- The neuron with the highest activation determines the predicted digit:
This structured approach demonstrates how neural networks model real-world problems, from binary classification to deep learning applications like face and handwriting recognition.
Implementation of Forward Propagation
- Coffee Roasting Example (Classification Task)
- Neural Network Architecture
- TensorFlow Implementation
- Forward Propagation Step-by-Step (NumPy Implementation)
- Artificial General Intelligence (AGI)
Coffee Roasting Example (Classification Task)
Imagine we want to classify coffee as either "Good" or "Bad" based on two factors:
- Temperature (°C)
- Roasting Time (minutes)
For simplicity, we define:
- Good coffee: If the temperature is between 190°C and 210°C and the roasting time is between 10 and 15 minutes.
- Bad coffee: Any other condition.
We collect the following data:
| Temperature (°C) | Roasting Time (min) | Quality (1 = Good, 0 = Bad) |
|---|---|---|
| 200 | 12 | 1 |
| 180 | 10 | 0 |
| 210 | 15 | 1 |
| 220 | 20 | 0 |
| 195 | 13 | 1 |
We will implement a simple neural network using TensorFlow to classify new coffee samples.
Neural Network Architecture
We construct a neural network using the following structure:
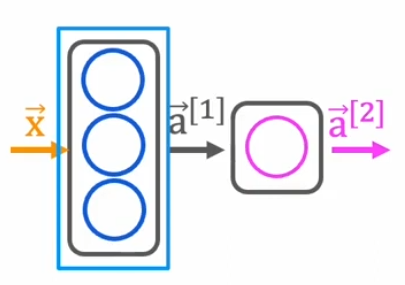
- Input Layer: Two neurons (temperature, time)
- Hidden Layer: Three neurons, activated with the sigmoid function
- Output Layer: One neuron, activated with the sigmoid function (binary classification)
TensorFlow Implementation
Step 1: Importing Libraries
import tensorflow as tf
import numpy as np
tensorflowis the core deep learning library that allows us to define and train neural networks.numpyis used for handling arrays and numerical operations efficiently.
Step 2: Defining Inputs and Outputs
X = np.array([[200, 12], [180, 10], [210, 15], [220, 20], [195, 13]], dtype=np.float32)
y = np.array([[1], [0], [1], [0], [1]], dtype=np.float32)
Xrepresents the input features (temperature and roasting time) as a NumPy array.yrepresents the expected output (1 for good coffee, 0 for bad coffee).dtype=np.float32ensures numerical stability and compatibility with TensorFlow.
Step 3: Building the Model
model = tf.keras.Sequential([
tf.keras.layers.Dense(3, activation='sigmoid', input_shape=(2,)),
tf.keras.layers.Dense(1, activation='sigmoid')
])
Sequential()creates a linear stack of layers.Dense(3, activation='sigmoid', input_shape=(2,))defines the hidden layer:- 3 neurons
- Sigmoid activation function
- Input shape of (2,) since we have two input features.
Dense(1, activation='sigmoid')defines the output layer with 1 neuron and sigmoid activation.
Step 4: Training the Model
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
model.fit(X, y, epochs=500, verbose=0)
compile()configures the model for training:adamoptimizer adapts the learning rate automatically.binary_crossentropyis used for binary classification problems.accuracymetric tracks how well the model classifies coffee samples.
fit(X, y, epochs=500, verbose=0)trains the model for 500 epochs (iterations over data).
Step 5: Making Predictions
new_coffee = np.array([[205, 14]], dtype=np.float32)
prediction = model.predict(new_coffee)
print("Prediction (Probability of Good Coffee):", prediction)
new_coffeecontains a new sample (205°C, 14 min) to classify.model.predict(new_coffee)computes the probability of the coffee being good.- The output is a probability (closer to 1 means good, closer to 0 means bad).
Forward Propagation Step-by-Step (NumPy Implementation)
We now implement forward propagation manually using NumPy to understand how TensorFlow executes it under the hood.
Initializing Weights and Biases
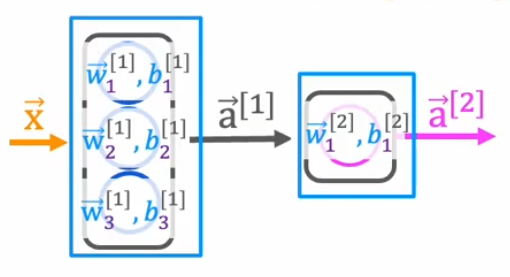
np.random.seed(42) # For reproducibility
W1 = np.random.randn(2, 4) # Weights for hidden layer (2 inputs -> 4 neurons)
b1 = np.random.randn(4) # Bias for hidden layer
W2 = np.random.randn(4, 1) # Weights for output layer (4 neurons -> 1 output)
b2 = np.random.randn(1) # Bias for output layer
np.random.randn()initializes weights and biases randomly from a normal distribution.W1andb1define the hidden layer parameters.W2andb2define the output layer parameters.
Forward Propagation Calculation
def sigmoid(z):
return 1 / (1 + np.exp(-z))
- This function applies the sigmoid activation function, which outputs values between 0 and 1.
def forward_propagation(X):
Z1 = np.dot(X, W1) + b1 # Linear transformation (Hidden Layer)
A1 = sigmoid(Z1) # Activation function (Hidden Layer)
Z2 = np.dot(A1, W2) + b2 # Linear transformation (Output Layer)
A2 = sigmoid(Z2) # Activation function (Output Layer)
return A2
np.dot(X, W1) + b1computes the weighted sum of inputs for the hidden layer.sigmoid(Z1)applies the activation function to introduce non-linearity.np.dot(A1, W2) + b2computes the weighted sum of outputs from the hidden layer.sigmoid(Z2)produces the final prediction.
# Testing with an example input
output = forward_propagation(np.array([[185, 10]]))
print(output)
This manually replicates TensorFlow's forward propagation but using pure NumPy.
Artificial General Intelligence (AGI)
AGI refers to AI that can perform any intellectual task a human can. Unlike current AI systems, AGI would adapt, learn, and generalize across different tasks without needing task-specific training.
Everyday Example: AGI vs. Narrow AI
- Narrow AI (Current AI): A chess-playing AI can defeat world champions but cannot drive a car.
- AGI: If a chess-playing AI was truly intelligent, it would learn how to drive just like a human without explicit programming.
Key Challenges in AGI
- Transfer Learning: Current AI requires large amounts of data. Humans learn with few examples.
- Common Sense Reasoning: AI struggles with simple logic like "If I drop a glass, it will break."
- Self-Learning: AGI must improve without needing human intervention.
Is AGI Possible?
- Some scientists believe AGI is decades away, while others argue it may never happen.
- Brain-inspired architectures (like Neural Networks) might be a stepping stone toward AGI.
Neural Network Training and Activation Functions
Understanding Loss Functions
Binary Crossentropy (BCE)
Binary crossentropy is commonly used for binary classification problems. It measures the difference between the predicted probability and the true label as follows:
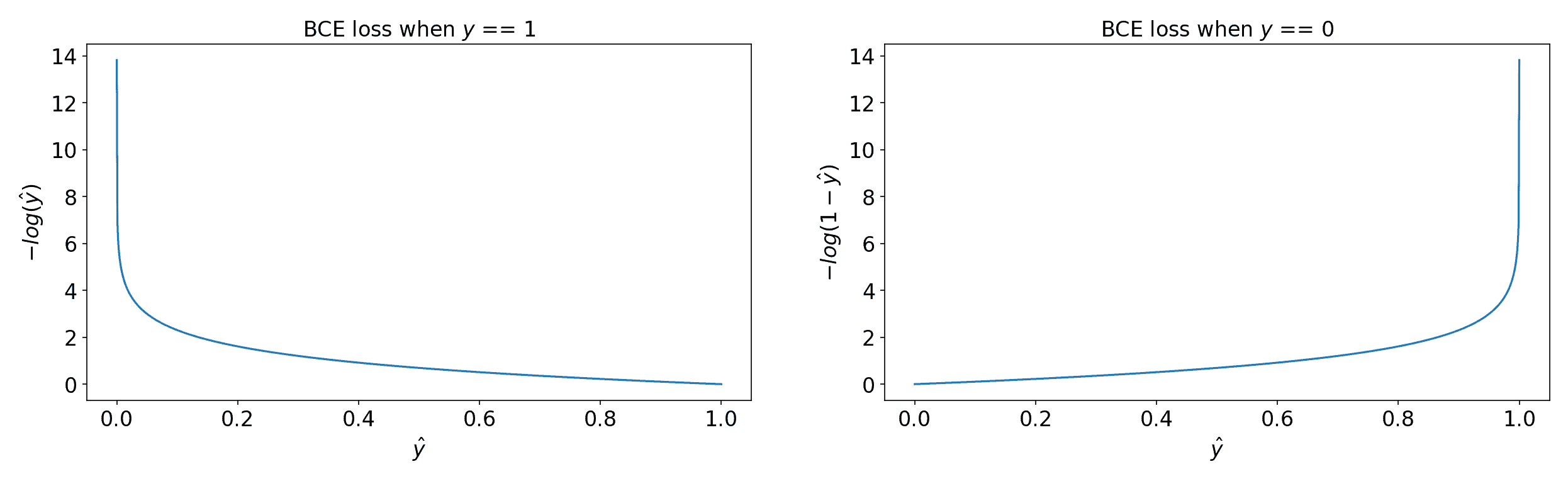
TensorFlow Implementation
import tensorflow as tf
loss_fn = tf.keras.losses.BinaryCrossentropy()
y_true = [1, 0, 1, 1]
y_pred = [0.9, 0.1, 0.8, 0.6]
loss = loss_fn(y_true, y_pred)
print("Binary Crossentropy Loss:", loss.numpy())
Mean Squared Error (MSE)
For regression problems, MSE calculates the average squared differences between actual and predicted values:
TensorFlow Implementation
mse_fn = tf.keras.losses.MeanSquaredError()
y_true = [3.0, -0.5, 2.0, 7.0]
y_pred = [2.5, 0.0, 2.1, 7.8]
mse_loss = mse_fn(y_true, y_pred)
print("Mean Squared Error Loss:", mse_loss.numpy())
Categorical Crossentropy (CCE)
Categorical crossentropy is used for multi-class classification problems where labels are one-hot encoded. The loss function is given by:
where is the number of classes.
TensorFlow Implementation
cce_fn = tf.keras.losses.CategoricalCrossentropy()
y_true = [[0, 0, 1], [0, 1, 0]] # One-hot encoded labels
y_pred = [[0.1, 0.2, 0.7], [0.2, 0.6, 0.2]] # Model predictions
cce_loss = cce_fn(y_true, y_pred)
print("Categorical Crossentropy Loss:", cce_loss.numpy())
Sparse Categorical Crossentropy (SCCE)
Sparse categorical crossentropy is similar to categorical crossentropy but used when labels are not one-hot encoded (i.e., they are integers instead of vectors).
TensorFlow Implementation
scce_fn = tf.keras.losses.SparseCategoricalCrossentropy()
y_true = [2, 1] # Integer labels
y_pred = [[0.1, 0.2, 0.7], [0.2, 0.6, 0.2]] # Model predictions
scce_loss = scce_fn(y_true, y_pred)
print("Sparse Categorical Crossentropy Loss:", scce_loss.numpy())
Choosing the Right Loss Function
| Problem Type | Suitable Loss Function | Example Application |
|---|---|---|
| Binary Classification | BinaryCrossentropy | Spam detection |
| Multi-class Classification (one-hot) | CategoricalCrossentropy | Image classification |
| Multi-class Classification (integer labels) | SparseCategoricalCrossentropy | Sentiment analysis |
| Regression | MeanSquaredError | House price prediction |
Each loss function serves a different purpose and is chosen based on the nature of the problem. For classification tasks, crossentropy-based losses are preferred, while for regression, MSE is commonly used. Understanding the structure of your dataset and the expected output format is crucial when selecting the right loss function.
Training Details Main Concepts
Epochs
An epoch represents one complete pass of the entire training dataset through the neural network. During each epoch, the model updates its weights based on the error calculated from the loss function.

- If we train for one epoch, the model sees each training sample exactly once.
- If we train for multiple epochs, the model repeatedly sees the same data and continuously updates its weights to improve performance.
Choosing the Number of Epochs
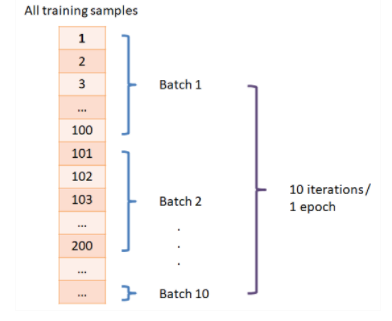
- Too Few Epochs → The model may underfit, meaning it has not learned enough patterns from the data.
- Too Many Epochs → The model may overfit, meaning it memorizes the training data but generalizes poorly to new data.
- The optimal number of epochs is typically determined using early stopping, which monitors validation loss and stops training when the loss starts increasing (a sign of overfitting).
TensorFlow Implementation
model.fit(X_train, y_train, epochs=50, batch_size=32, validation_data=(X_val, y_val))
Batch Size
Instead of feeding the entire dataset into the model at once, training is performed in smaller subsets called batches.
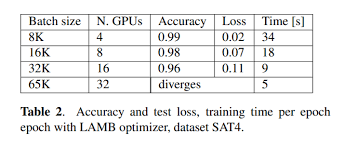
Key Concepts:
- Batch Size: The number of training samples processed before updating the model's weights.
- Iteration: One update of the model’s weights after processing a batch.
- Steps Per Epoch: If we have
Ntraining samples and batch sizeB, then the number of steps per epoch is N/B.
Choosing Batch Size
- Small Batch Sizes (e.g., 16, 32):
- Require less memory.
- Provide noisy but effective updates (better generalization).
- Large Batch Sizes (e.g., 256, 512, 1024):
- Require more memory.
- Lead to smoother but potentially less generalized updates.
TensorFlow Implementation
model.fit(X_train, y_train, epochs=20, batch_size=64)
Validation Data
A validation set is a separate portion of the dataset that is not used for training. It helps monitor the model's performance and detect overfitting.
Differences Between Training, Validation, and Test Data:
| Data Type | Purpose |
|---|---|
| Training Set | Used for updating model weights during training. |
| Validation Set | Used to tune hyperparameters and detect overfitting. |
| Test Set | Used to evaluate final model performance on unseen data. |
How to Split Data:
A common split is 80% training, 10% validation, 10% test, but this can vary based on dataset size.
TensorFlow Implementation
from sklearn.model_selection import train_test_split
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)
model.fit(X_train, y_train, epochs=30, batch_size=32, validation_data=(X_val, y_val))
Activation Functions
1. Why Do We Need Activation Functions?
Without an activation function, a neural network with multiple layers behaves like a single-layer linear model because:
is just a linear transformation. Activation functions introduce non-linearity, allowing the network to learn complex patterns.
If we do not apply non-linearity, no matter how many layers we stack, the final output remains a linear function of the input. Activation functions solve this by enabling the model to approximate complex, non-linear relationships.
2. Common Activation Functions
Sigmoid (Logistic Function)
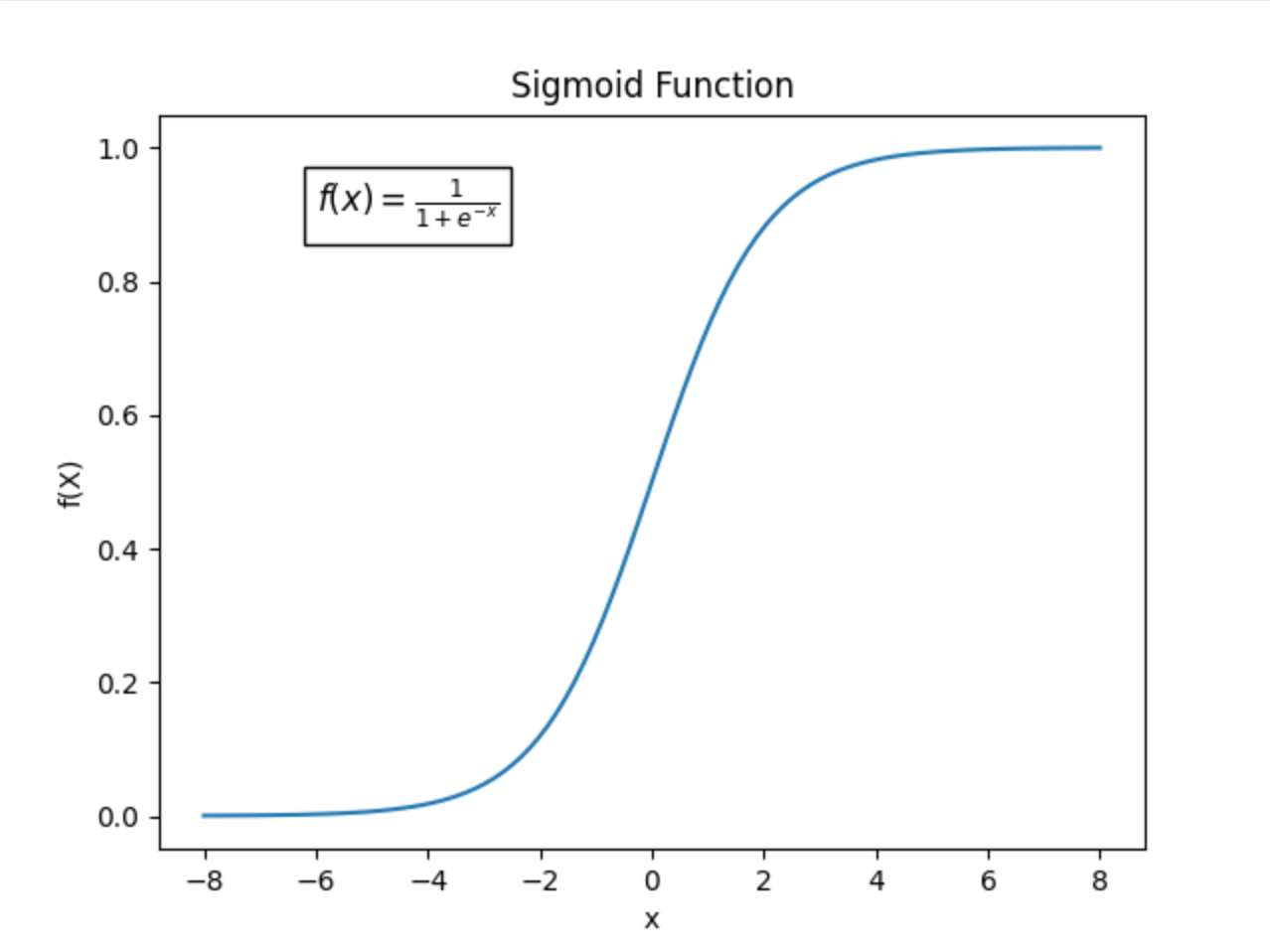
- Range: (0, 1)
- Used in: Binary classification problems
- Pros: Outputs can be interpreted as probabilities.
- Cons: Vanishing gradients for very large or very small values of ( x ), making training slow.
ReLU (Rectified Linear Unit)
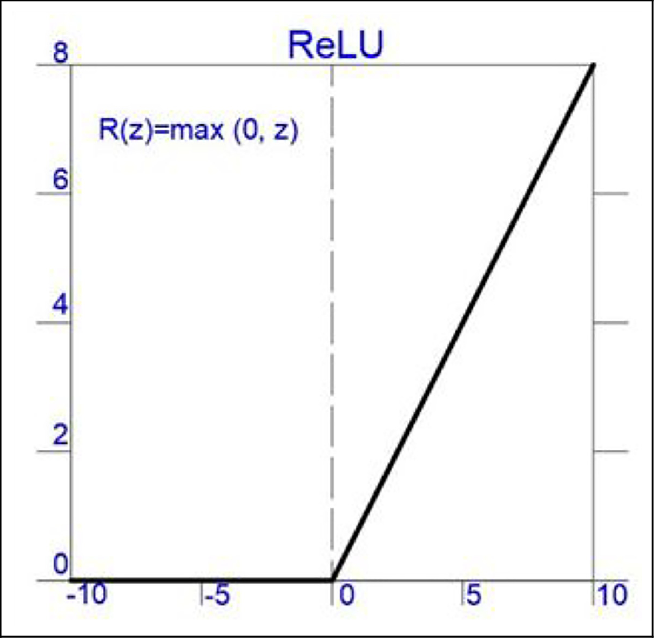
- Range: [0, ∞)
- Used in: Hidden layers of deep neural networks.
- Pros: Helps with gradient flow and avoids vanishing gradients.
- Cons: Can suffer from dying ReLU problem (where neurons output 0 and stop learning if input is negative).
Leaky ReLU
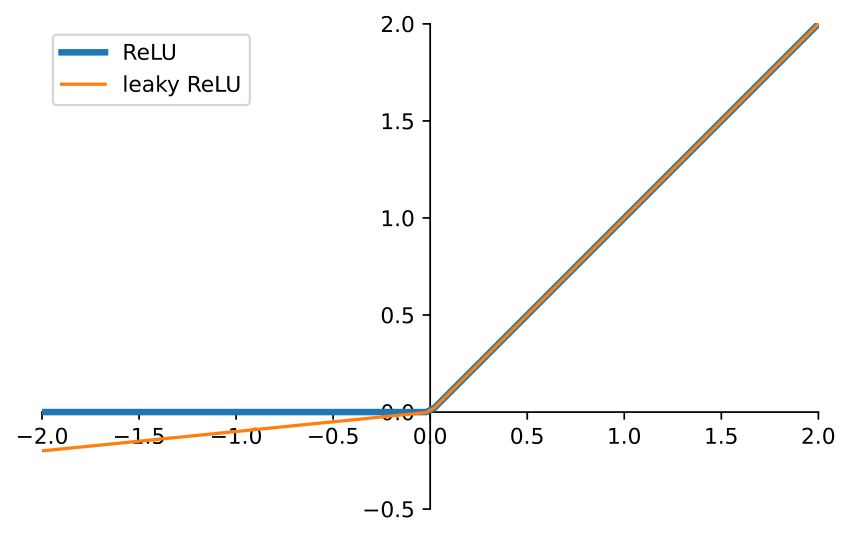
- Range: (-∞, ∞)
- Used in: Hidden layers as an alternative to ReLU.
- Pros: Prevents the dying ReLU problem.
- Cons: Small negative slope may still lead to slow learning.
Softmax
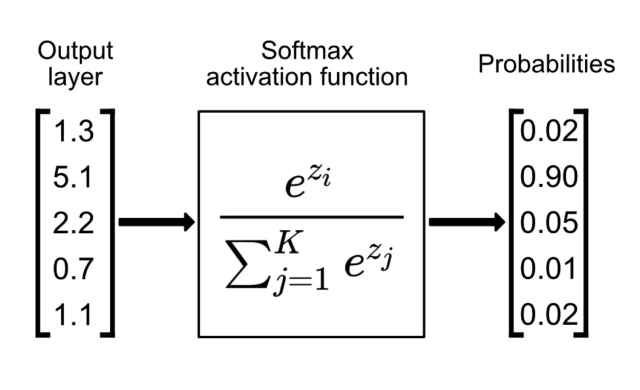
- Used in: Multi-class classification (output layer).
- Pros: Outputs a probability distribution (each class gets a probability between 0 and 1, summing to 1).
- Cons: Can lead to numerical instability when exponentiating large numbers.
Linear Activation
- Used in: Regression problems (output layer).
- Pros: No constraints on output values.
- Cons: Not useful for classification since it doesn’t map values to a specific range.
3. Choosing the Right Activation Function
| Layer | Recommended Activation Function | Explanation |
|---|---|---|
| Hidden Layers | ReLU (or Leaky ReLU if ReLU is dying) | Helps with deep networks by maintaining gradient flow |
| Output Layer (Binary Classification) | Sigmoid | Outputs probabilities for two-class classification |
| Output Layer (Multi-Class Classification) | Softmax | Converts logits into probability distributions |
| Output Layer (Regression) | Linear | Directly outputs numerical values |
Softmax vs. Sigmoid: Key Differences
- Sigmoid is mainly used for binary classification, mapping values to (0,1), which can be interpreted as class probabilities.
- Softmax is used for multi-class classification, producing a probability distribution over multiple classes.
If you use sigmoid for multi-class problems, each output node will act independently, making it difficult to ensure they sum to 1. Softmax ensures that outputs sum to 1, providing a clearer probabilistic interpretation.
Improved Implementation of Softmax
Why Use Linear Instead of Softmax in the Output Layer?
When implementing a neural network for classification, we often pass logits (raw outputs) directly into the loss function instead of applying softmax explicitly.
Mathematically, if we apply softmax explicitly:
where ( \sigma(z) ) is the softmax function.
However, if we pass raw logits (without softmax) into the cross-entropy loss function, TensorFlow applies the log-softmax trick internally:
This avoids computing large exponentials, improving numerical stability and reducing computation cost.
TensorFlow Implementation
Instead of:
model = tf.keras.Sequential([
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax') # Explicit softmax
])
model.compile(loss=tf.keras.losses.SparseCategoricalCrossentropy(), optimizer='adam')
Use:
model = tf.keras.Sequential([
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(10) # No activation here!
])
model.compile(loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True), optimizer='adam')
This allows TensorFlow to handle softmax internally, avoiding unnecessary computation and improving numerical precision.
Optimizers and Layer Types
- Optimizers in Deep Learning
- Choosing the Right Optimizer
- Gradient Descent (GD)
- Stochastic Gradient Descent (SGD)
- Stochastic Gradient Descent with Momentum (SGD-Momentum)
- Mini-Batch Gradient Descent
- Adagrad (Adaptive Gradient Descent)
- RMSprop (Root Mean Square Propagation)
- AdaDelta
- Adam (Adaptive Moment Estimation)
- Hands-on Optimizers
- Table Analysis
- Conclusion
- Additional Layer Types in Neural Networks
Optimizers in Deep Learning
Optimizers play a crucial role in training deep learning models by adjusting the model parameters to minimize the loss function. Different optimization algorithms have been developed to improve convergence speed, accuracy, and stability. In this article, we explore various optimizers used in deep learning, their mathematical formulations, and practical implementations.
Choosing the Right Optimizer
Choosing the right optimizer depends on several factors, including:
- The nature of the dataset
- The complexity of the model
- The presence of noisy gradients
- The required computational efficiency
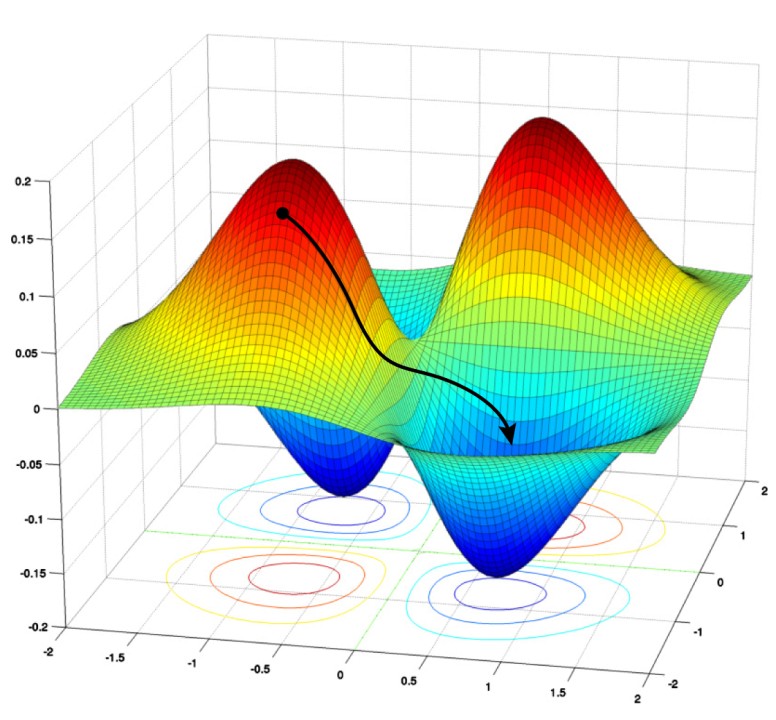
Below, we examine different types of optimizers along with their mathematical formulations.
Gradient Descent (GD)
Mathematical Formulation
Gradient Descent updates model parameters iteratively using the gradient of the loss function :
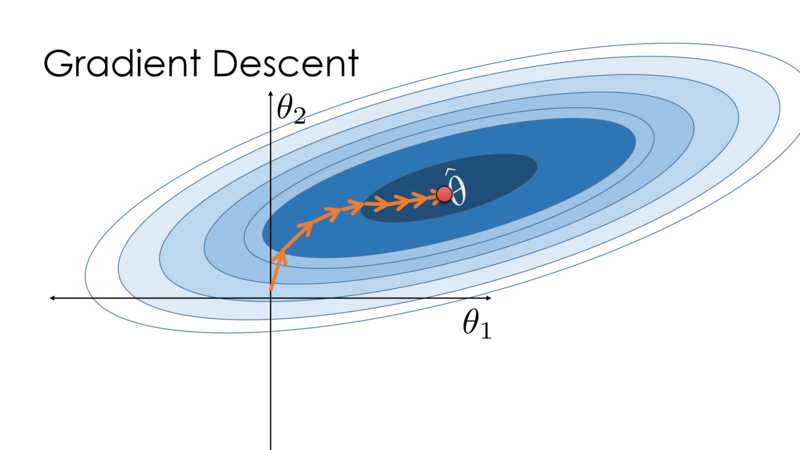
where:
- is the learning rate
- is the gradient of the loss function
Characteristics
- Computes gradient over the entire dataset
- Slow for large datasets
- Prone to getting stuck in local minima
Stochastic Gradient Descent (SGD)
Gradient descent struggles with massive datasets, making stochastic gradient descent (SGD) a better alternative. Unlike standard gradient descent, SGD updates model parameters using small, randomly selected data batches, improving computational efficiency.
SGD initializes parameters and learning rate , then shuffles data at each iteration, updating based on mini-batches. This introduces noise, requiring more iterations to converge, but still reduces overall computation time compared to full-batch gradient descent.
For large datasets where speed matters, SGD is preferred over batch gradient descent.
Mathematical Formulation
Instead of computing the gradient over the entire dataset, SGD updates using a single data point:
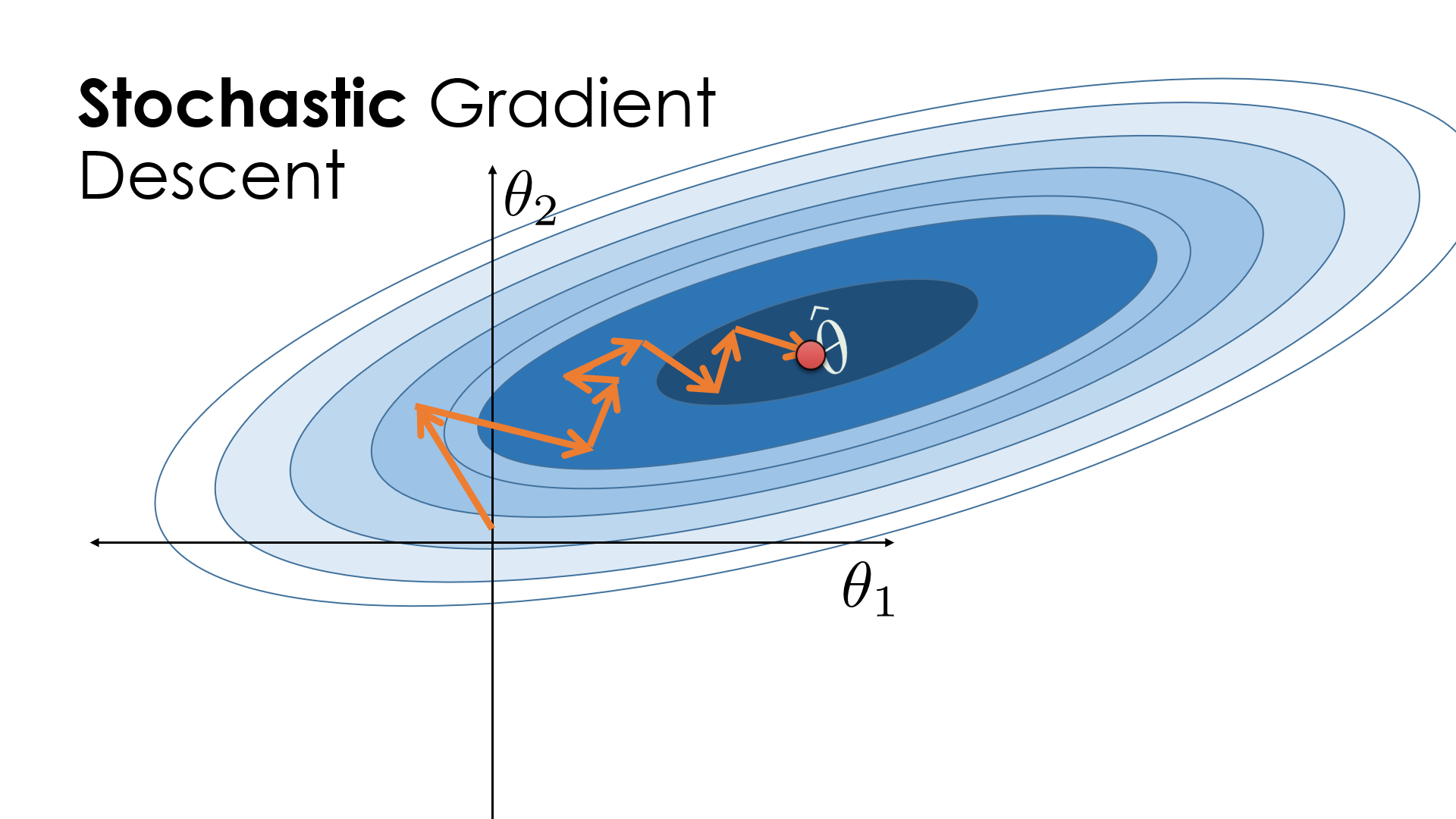
where is a single training example.
Characteristics
- Faster than full-batch gradient descent
- High variance in updates
- Introduces noise, which can help escape local minima
Stochastic Gradient Descent with Momentum (SGD-Momentum)
SGD follows a noisy optimization path, requiring more iterations and longer computation time. To speed up convergence, SGD with momentum is used.
Momentum helps stabilize updates by adding a fraction of the previous update to the current one, reducing oscillations and accelerating convergence. However, a high momentum term requires lowering the learning rate to avoid overshooting the optimal minimum.
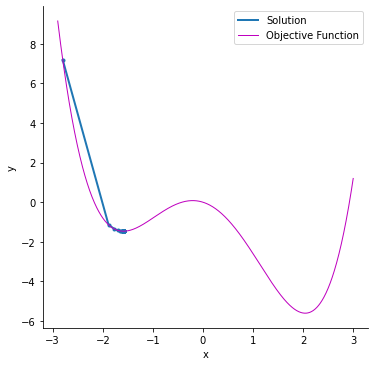
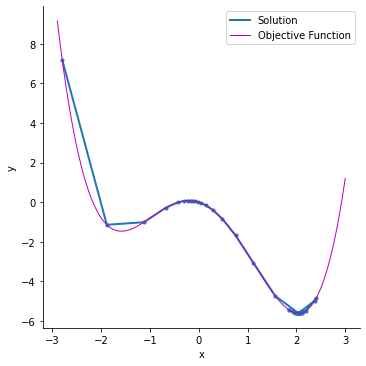
While momentum improves speed, too much momentum can cause instability and poor accuracy. Proper tuning is essential for effective optimization.
Mathematical Formulation
Momentum helps accelerate SGD by maintaining a velocity term:
where:
- is the momentum term
- is a momentum coefficient (typically 0.9)
Characteristics
- Reduces oscillations
- Faster convergence
Mini-Batch Gradient Descent
Mini-batch gradient descent optimizes training by using a subset of data instead of the entire dataset, reducing the number of iterations needed. This makes it faster than both stochastic and batch gradient descent while being more efficient and memory-friendly.
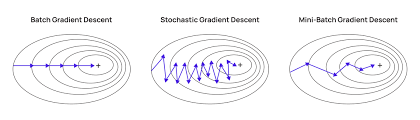
Key Advantages
- Balances speed and accuracy by reducing noise compared to SGD but keeping updates more dynamic than batch gradient descent.
- Doesn’t require loading all data into memory, improving implementation efficiency.
Limitations
- Requires tuning the mini-batch size (typically 32) for optimal accuracy.
- May lead to poor final accuracy in some cases, requiring alternative approaches.
Mathematical Formulation
Instead of updating with the entire dataset or a single example, mini-batch GD uses a small batch of samples:
Adagrad (Adaptive Gradient Descent)
Adagrad differs from other gradient descent algorithms by using a unique learning rate for each iteration, adjusting based on parameter changes. Larger parameter updates lead to smaller learning rate adjustments, making it effective for datasets with both sparse and dense features.
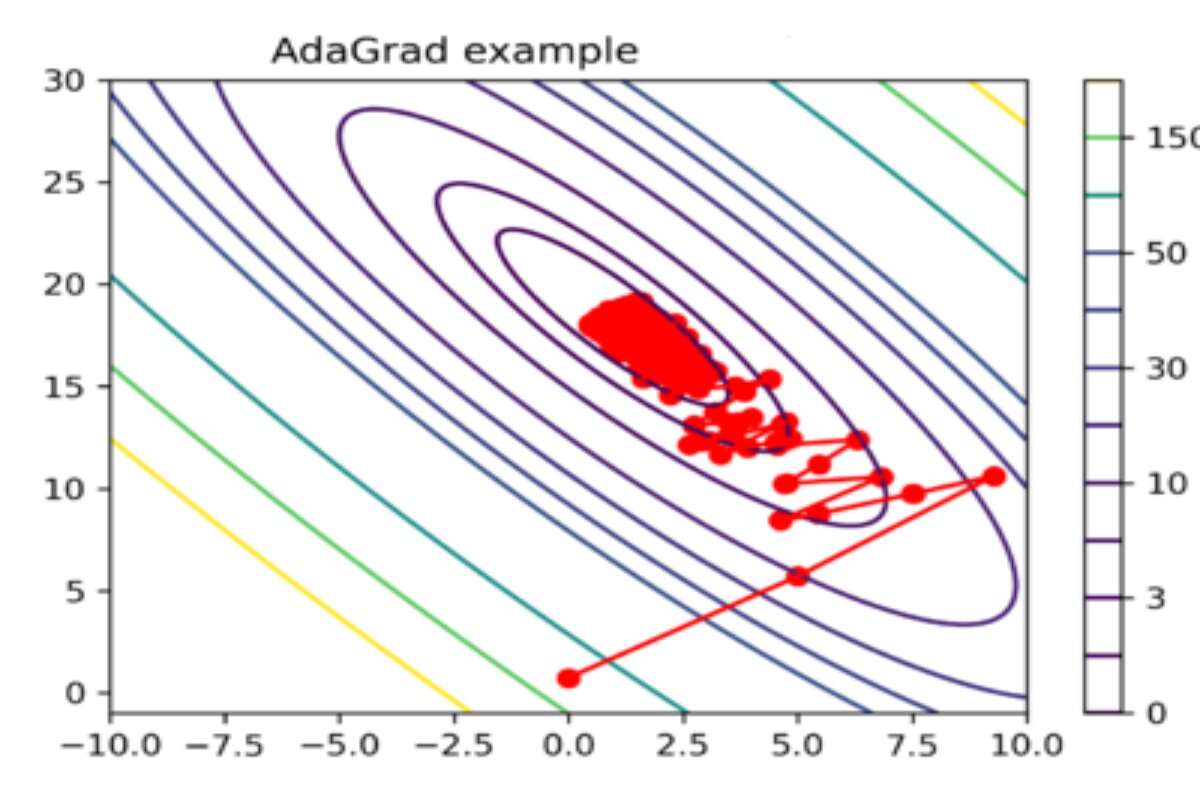
Key Advantages
- Eliminates manual learning rate tuning by adapting automatically.
- Faster convergence compared to standard gradient descent methods.
Limitations
- Aggressively reduces the learning rate over time, which can slow learning and harm accuracy.
- The accumulation of squared gradients in the denominator causes the learning rate to become too small, limiting further model improvements.
Mathematical Formulation
Adagrad adapts learning rates for each parameter:
where accumulates past squared gradients:
Characteristics
- Suitable for sparse data
- Learning rate decreases over time
RMSprop (Root Mean Square Propagation)
RMSProp improves stability by adapting step sizes per weight, preventing large gradient fluctuations. It maintains a moving average of squared gradients to adjust learning rates dynamically.
Mathematical Formulation
Pros
- Faster convergence with smoother updates.
- Less tuning than other gradient descent variants.
- More stable than Adagrad by preventing extreme learning rate decay.
Cons
- Requires manual learning rate tuning, and default values may not always be optimal.
AdaDelta
Mathematical Formulation
AdaDelta modifies Adagrad by using an exponentially decaying average of past squared gradients:
where is the moving average.
Characteristics
- Addresses diminishing learning rates in Adagrad
- No need to manually set a learning rate
Adam (Adaptive Moment Estimation)
Adam (Adaptive Moment Estimation) is a widely used deep learning optimizer that extends SGD by dynamically adjusting learning rates for each weight. It combines AdaGrad and RMSProp to balance adaptive learning rates and stable updates.
Mathematical Formulation
Adam combines momentum and RMSprop:
where and are bias-corrected estimates.
Key Features
- Uses first (mean) and second (variance) moments of gradients.
- Faster convergence with minimal tuning.
- Low memory usage and efficient computation.
Downsides
- Prioritizes speed over generalization, making SGD better for some cases.
- May not always be ideal for every dataset.
Adam is the default choice for many deep learning tasks but should be selected based on the dataset and training requirements.
Hands-on Optimizers
Import Necessary Libraries
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
(x_train, y_train), (x_test, y_test) = mnist.load_data()
print(x_train.shape, y_train.shape)
Load the Dataset
x_train= x_train.reshape(x_train.shape[0],28,28,1)
x_test= x_test.reshape(x_test.shape[0],28,28,1)
input_shape=(28,28,1)
y_train=keras.utils.to_categorical(y_train)#,num_classes=)
y_test=keras.utils.to_categorical(y_test)#, num_classes)
x_train= x_train.astype('float32')
x_test= x_test.astype('float32')
x_train /= 255
x_test /=255
Build the Model
batch_size=64
num_classes=10
epochs=10
def build_model(optimizer):
model=Sequential()
model.add(Conv2D(32,kernel_size=(3,3),activation='relu',input_shape=input_shape))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy, optimizer= optimizer, metrics=['accuracy'])
return model
Train the Model
optimizers = ['Adadelta', 'Adagrad', 'Adam', 'RMSprop', 'SGD']
for i in optimizers:
model = build_model(i)
hist=model.fit(x_train, y_train, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_test,y_test))
Table Analysis
| Optimizer | Epoch 1 (Val Acc | Val Loss) | Epoch 5 (Val Acc | Val Loss) | Epoch 10 (Val Acc | Val Loss) | Total Time |
|---|---|---|---|---|---|---|---|
| Adadelta | .4612 | 2.2474 | .7776 | 1.6943 | .8375 | 0.9026 | 8:02 min |
| Adagrad | .8411 | .7804 | .9133 | .3194 | .9286 | 0.2519 | 7:33 min |
| Adam | .9772 | .0701 | .9884 | .0344 | .9908 | .0297 | 7:20 min |
| RMSprop | .9783 | .0712 | .9846 | .0484 | .9857 | .0501 | 10:01 min |
| SGD with momentum | .9168 | .2929 | .9585 | .1421 | .9697 | .1008 | 7:04 min |
| SGD | .9124 | .3157 | .9569 | 1.451 | .9693 | .1040 | 6:42 min |
The above table shows the validation accuracy and loss at different epochs. It also contains the total time that the model took to run on 10 epochs for each optimizer. From the above table, we can make the following analysis.
- The adam optimizer shows the best accuracy in a satisfactory amount of time.
- RMSprop shows similar accuracy to that of Adam but with a comparatively much larger computation time.
- Surprisingly, the SGD algorithm took the least time to train and produced good results as well. But to reach the accuracy of the Adam optimizer, SGD will require more iterations, and hence the computation time will increase.
- SGD with momentum shows similar accuracy to SGD with unexpectedly larger computation time. This means the value of momentum taken needs to be optimized.
- Adadelta shows poor results both with accuracy and computation time.
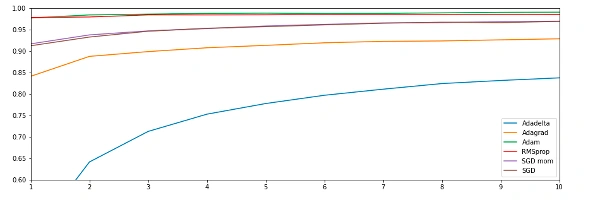
You can analyze the accuracy of each optimizer with each epoch from the above graph.
Conclusion
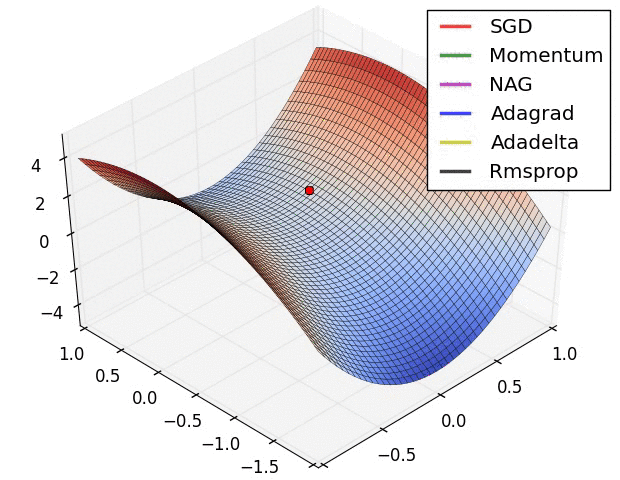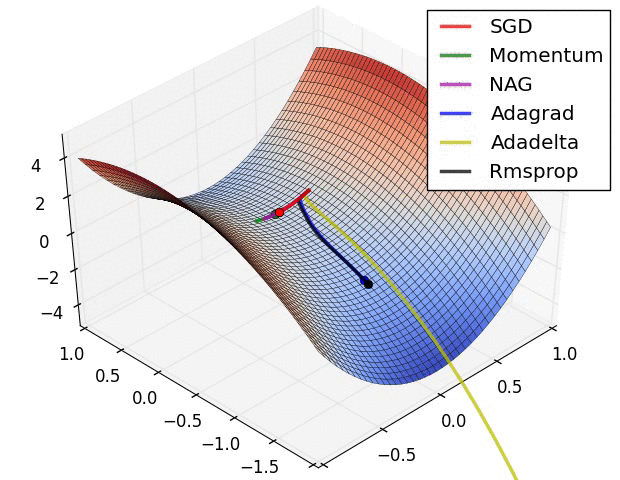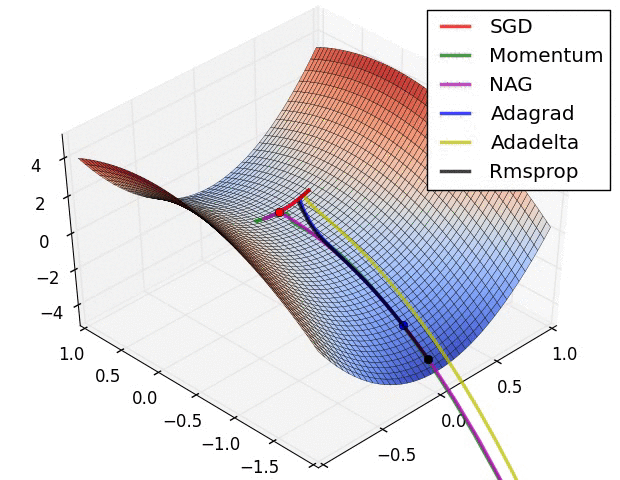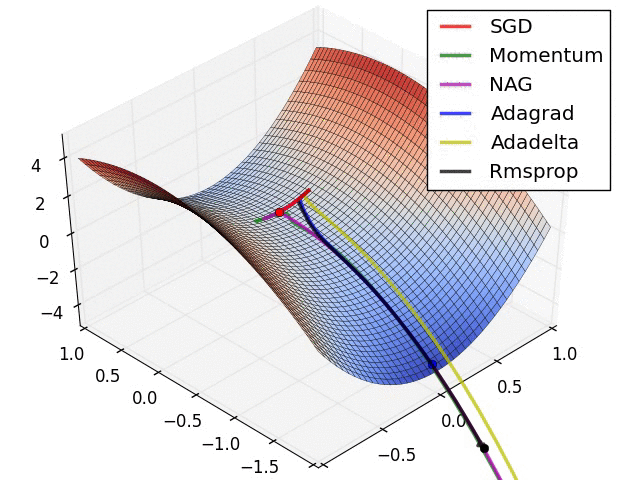
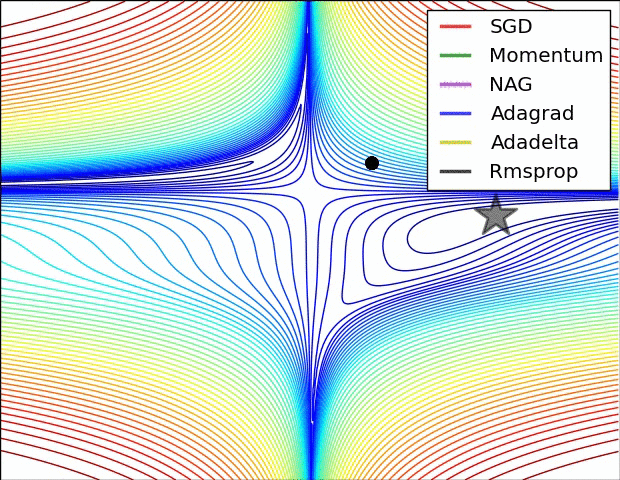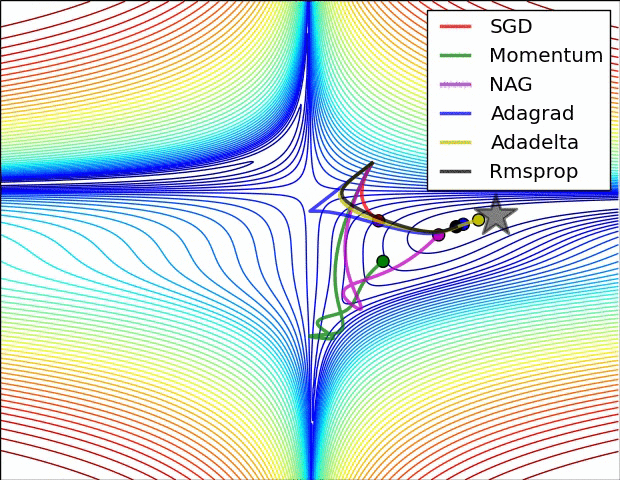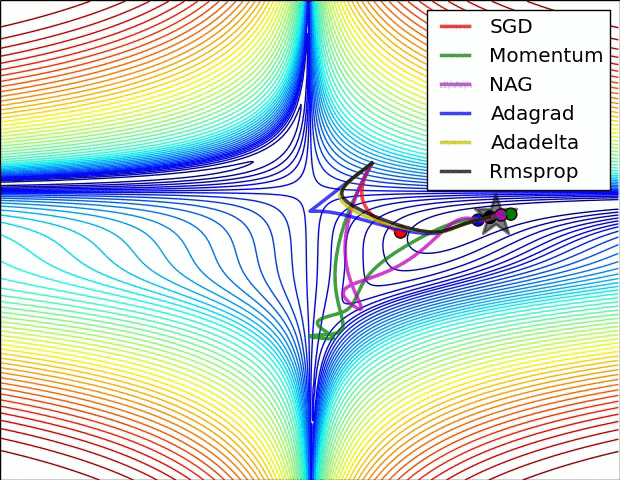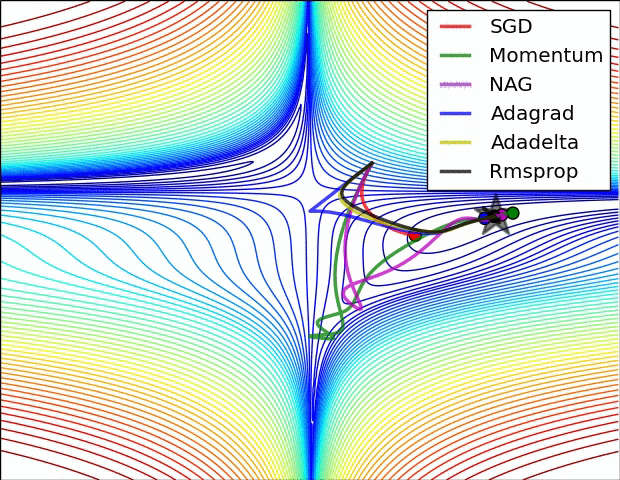
Different optimizers offer unique advantages based on the dataset and model architecture. While SGD is the simplest, Adam is often preferred for deep learning tasks due to its adaptive learning rate and momentum.
By understanding these optimizers, you can fine-tune deep learning models for optimal performance!
Additional Layer Types in Neural Networks
In deep learning, different layer types serve distinct purposes, helping neural networks learn complex representations. This section explores various layer types, their mathematical foundations, and practical implementations.
Dense Layer (Fully Connected Layer)
A Dense layer is a fundamental layer where each neuron is connected to every neuron in the previous layer.
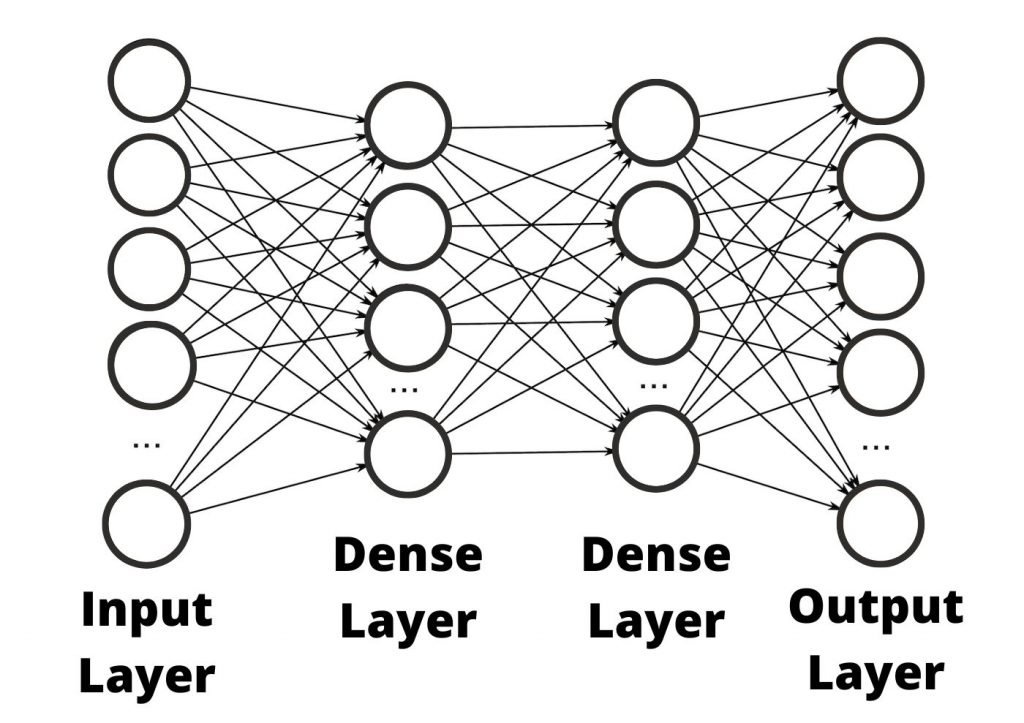
Mathematical Representation:
Given an input vector of size , weights of size , and bias of size , the output is calculated as:
where is an activation function such as ReLU, Sigmoid, or Softmax.
Implementation in TensorFlow:
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
model = Sequential([
Dense(64, activation='relu', input_shape=(100,)),
Dense(32, activation='relu'),
Dense(10, activation='softmax')
])
model.summary()
Convolutional Layer (Conv2D)
A Convolutional layer is used in image processing, applying filters (kernels) to extract features from input images.
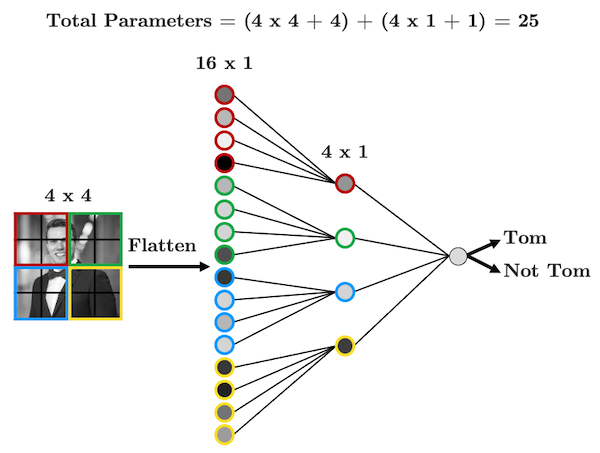
Mathematical Representation:
For an input image and a filter , the convolution operation is defined as:
Implementation in TensorFlow:
from tensorflow.keras.layers import Conv2D
model = Sequential([
Conv2D(32, kernel_size=(3,3), activation='relu', input_shape=(28,28,1)),
Conv2D(64, kernel_size=(3,3), activation='relu'),
])
model.summary()
Pooling Layer (MaxPooling & AveragePooling)
Pooling layers reduce dimensionality while preserving important features.
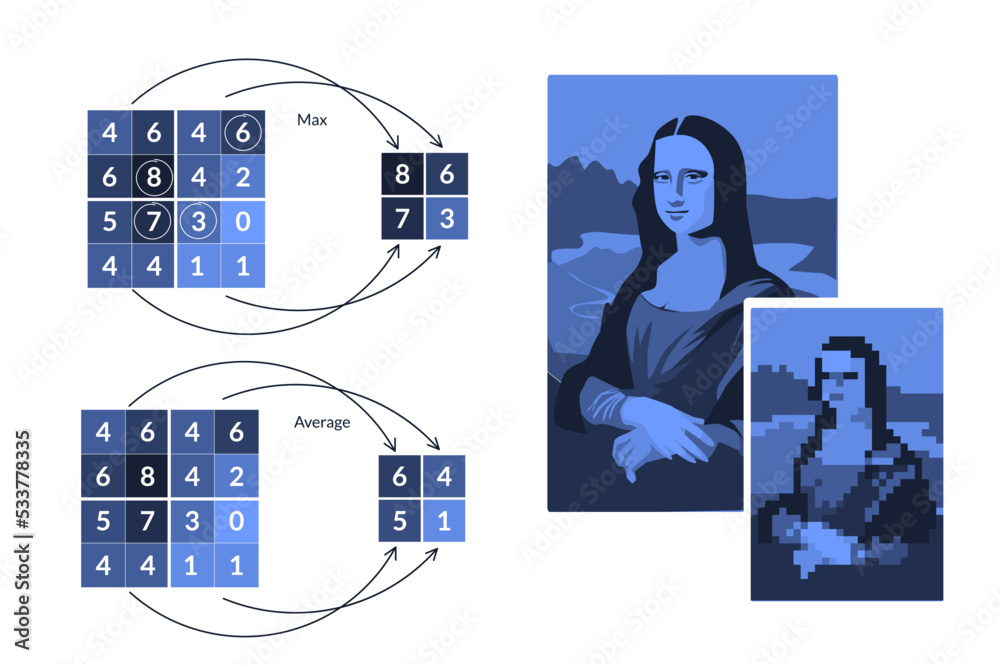
Max Pooling:
Average Pooling:
Implementation:
from tensorflow.keras.layers import MaxPooling2D, AveragePooling2D
model = Sequential([
MaxPooling2D(pool_size=(2,2)),
AveragePooling2D(pool_size=(2,2))
])
model.summary()
Recurrent Layer (RNN, LSTM, GRU)
Recurrent layers process sequential data by maintaining memory of past inputs.
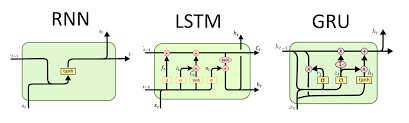
RNN Mathematical Model:
LSTM Update Equations:
Implementation:
from tensorflow.keras.layers import SimpleRNN, LSTM, GRU
model = Sequential([
LSTM(64, return_sequences=True, input_shape=(100, 10)),
GRU(32)
])
model.summary()
Dropout Layer
The Dropout layer randomly sets a fraction of input units to 0 to prevent overfitting.
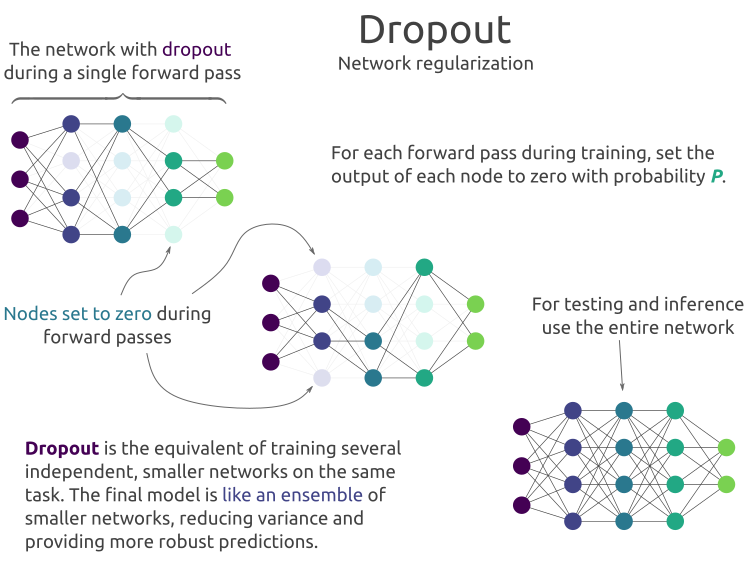
Mathematical Explanation:
During training, for each neuron, the probability of being kept is :
Implementation:
from tensorflow.keras.layers import Dropout
model = Sequential([
Dense(128, activation='relu'),
Dropout(0.5),
Dense(64, activation='relu'),
Dropout(0.3),
Dense(10, activation='softmax')
])
model.summary()
Comparison Table
| Layer Type | Purpose | Typical Use Case |
|---|---|---|
| Dense | Fully connected layer | General deep learning models |
| Conv2D | Feature extraction | Image processing |
| Pooling | Downsampling | CNNs to reduce size |
| RNN | Sequential processing | Time-series, NLP |
| LSTM/GRU | Long-term memory retention | Language models |
| Dropout | Overfitting prevention | Regularization in deep networks |
Conclusion
Understanding different types of layers is crucial in designing effective deep learning models. Choosing the right layers based on the data type and problem domain significantly impacts model performance. Experimenting with combinations of these layers is key to optimizing results.
Model Evaluation, Selection, and Improvement
- Evaluating a Model
- Model Selection and Training/Validation/Test Sets
- Diagnosing Bias and Variance
- Regularization and Bias-Variance Tradeoff
- Establishing a Baseline Level of Performance
- Iterative Loop of ML Development
- Adding Data: Data Augmentation & Synthesis
- Transfer Learning: Using Data from a Different Task
- Error Metrics for Skewed Datasets
Evaluating a Model
A metric is a numerical measure used to assess the performance of a model on a given dataset. Metrics help quantify how well a model is making predictions and whether it meets the desired objectives. The choice of metric depends on the nature of the problem:
- For classification tasks, we often measure how accurately a model assigns labels.
- For regression tasks, we evaluate how close the model's predictions are to actual values.
- In other domains like natural language processing (NLP) or computer vision, specialized metrics are used.
However, a high metric value does not always mean a model is truly effective. For example:
- In an imbalanced dataset, accuracy might be misleading. A model predicting the majority class 100% of the time can have high accuracy but perform poorly overall.
- A regression model with a low mean squared error (MSE) might still fail in real-world applications if it makes large errors in critical cases.
Key Metrics for Model Evaluation
Classification Metrics
- Accuracy: Measures the percentage of correctly predicted instances.
- Precision: The fraction of true positive predictions among all positive predictions.
- Recall: The fraction of actual positives correctly identified.
- F1-score: The harmonic mean of precision and recall, useful for imbalanced datasets.
- ROC-AUC (Receiver Operating Characteristic - Area Under Curve): Evaluates the model’s ability to distinguish between classes.
Regression Metrics
- Mean Squared Error (MSE): Measures the average squared difference between predicted and actual values.
- Mean Absolute Error (MAE): Measures the average absolute difference.
- R-squared (R²): Indicates how well the model explains variance in the data.
Other Metrics
- Log loss: Used for probabilistic classification models.
- BLEU score: Measures similarity in NLP tasks.
- Intersection over Union (IoU): Used in object detection to measure overlap between predicted and actual bounding boxes.
Choosing the Right Metric
Suppose we are building a spam classifier. If 99% of emails are non-spam, a naive model predicting "not spam" for all emails will have 99% accuracy but be completely useless. In this case, precision and recall are more meaningful metrics because they tell us how well the model detects actual spam emails without too many false positives.
Thus, choosing the right metric is just as important as achieving a high score. A well-performing model is one that aligns with the real-world objective of the task.
Model Selection and Training/Validation/Test Sets
Selecting the right model is essential for achieving high performance on unseen data. A model that performs well on training data but poorly on new data is overfitting, while a model that is too simple may underfit. To properly evaluate a model and fine-tune its performance, we split the dataset into three key subsets:
Training Set
The training set is the portion of the data used to train the machine learning model. The model learns patterns from this data by adjusting its internal parameters. However, evaluating the model only on the training set is misleading because the model might memorize the data instead of generalizing from it.
Validation Set
The validation set is a separate portion of the dataset that is used to tune hyperparameters and select the best model architecture. Hyperparameters are external configuration settings that are not learned by the model but instead set manually or through automated search methods. Examples of hyperparameters include:
- Learning rate
- Number of hidden layers in a neural network
- Regularization parameters (L1, L2)
- Batch size
By testing different hyperparameter values on the validation set, we can find the combination that leads to the best generalization performance. However, if the validation set is too small or used excessively for tuning, the model might start overfitting to it.
Test Set
The test set is used only once, after model training and hyperparameter tuning, to evaluate the final model's performance. The test set should remain completely unseen during training and validation to provide an unbiased estimate of how the model will perform on real-world data.
Cross-Validation
Cross-validation is a technique to make better use of available data and improve model selection. Instead of relying on a single validation set, we divide the dataset into multiple subsets and perform training and validation multiple times. The most common approach is k-fold cross-validation, which works as follows:
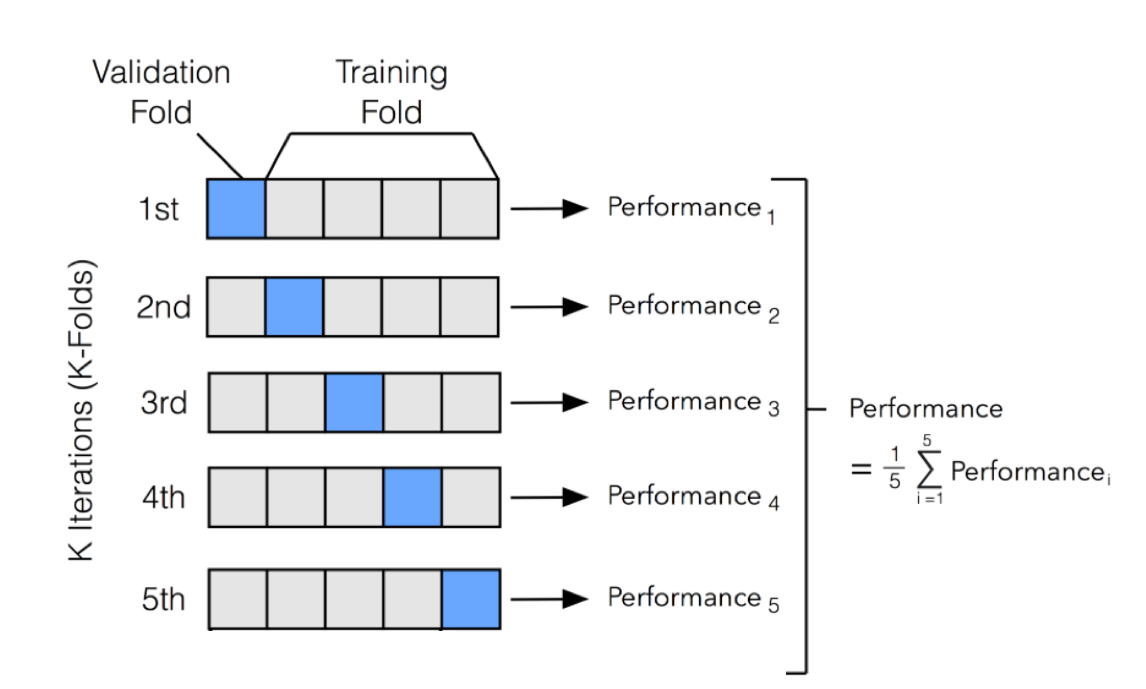
- The dataset is divided into k equal-sized folds.
- The model is trained on k-1 folds and validated on the remaining one.
- This process is repeated k times, with each fold serving as the validation set once.
- The final performance metric is the average of all validation scores.
For example, in 5-fold cross-validation, the dataset is split into 5 parts. The model is trained on 4 parts and validated on the remaining one, and this process repeats until each part has been used as a validation set once. This reduces the risk of selecting a model that performs well on just one specific validation set but poorly on unseen data.
Cross-validation is especially useful when working with small datasets since it allows more efficient use of data. However, it can be computationally expensive, especially for deep learning models, where training is time-consuming.
By using training, validation, and test sets appropriately—along with cross-validation where necessary—we can make informed decisions about model selection and ensure good generalization to new data.
Diagnosing Bias and Variance
Bias and variance are two key factors that determine a model’s ability to generalize to unseen data. To understand these concepts, let’s analyze the simple linear model:
A well-performing model should generalize well, meaning it captures the essential patterns in the data without memorizing noise. Let's break this down using the equation.

| Issue | Description | Effects | Impact of More Data |
|---|---|---|---|
| High Bias (Underfitting) | Model is too simple and cannot capture underlying patterns. | - Poor performance on both training and test sets. - Model is too simplistic. | Increasing training data does not improve performance. |
| High Variance (Overfitting) | Model is too complex and memorizes training data, including noise. | - Training error is very low, but test error is high. - Model learns noise instead of actual patterns. | Increasing training data can help generalization. |
Regularization and Bias-Variance Tradeoff
To prevent overfitting, we introduce regularization, which penalizes large weights.
The regularized loss function:
where:
- is the original loss function (e.g., Mean Squared Error),
- is the regularization strength,
- is the penalty term (L1 or L2).
Effect of Regularization
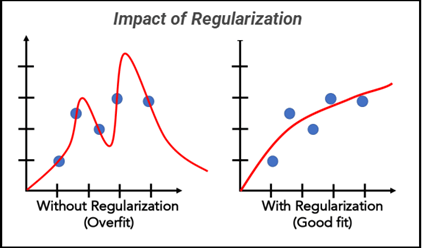
- If is too low, the model can overfit ( values become large).
- If is too high, the model becomes too simple ( values shrink too much).
- The ideal value balances bias and variance.
Establishing a Baseline Level of Performance
A baseline model helps measure improvement. Common baselines include:
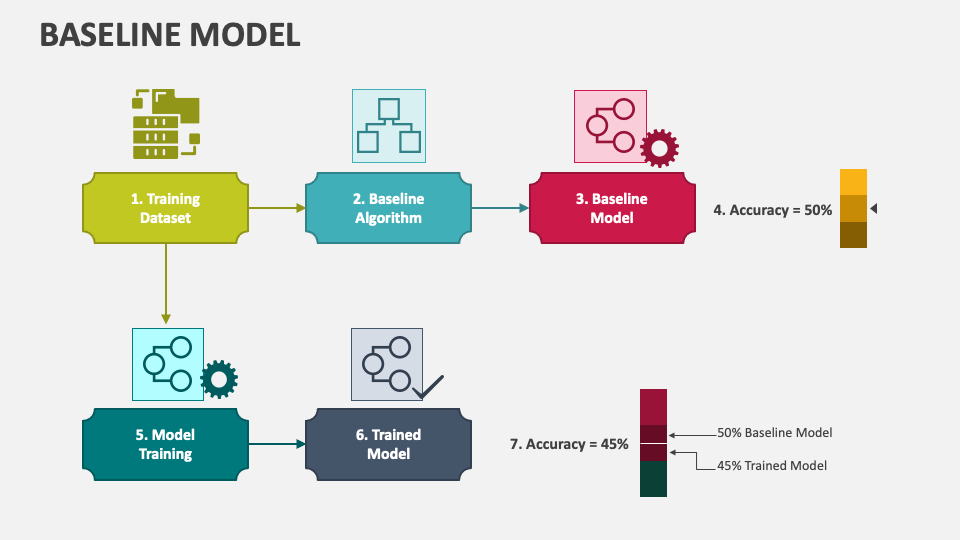
- Random classifiers (for classification tasks)
- Mean predictions (for regression tasks)
- Simple heuristic-based methods
A model must outperform the baseline to be considered useful.
Iterative Loop of ML Development
Machine learning development follows an iterative cycle:
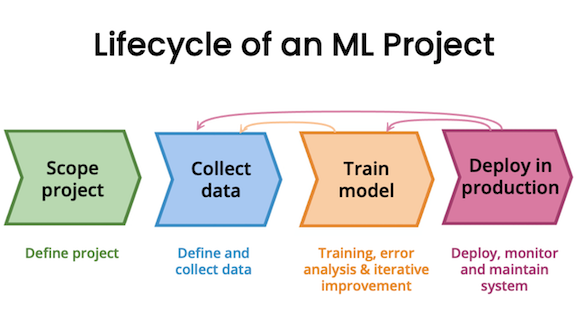
- Train a baseline model.
- Diagnose bias/variance errors.
- Adjust model complexity, regularization, or data strategy.
- Repeat until performance is satisfactory.
Adding Data: Data Augmentation & Synthesis
One of the most effective ways to improve a model’s generalization ability is by increasing the amount of training data. More data helps the model learn patterns that are not specific to the training set, reducing overfitting and improving robustness.
Data Augmentation
Data Augmentation refers to artificially increasing the size of the training dataset by applying transformations to existing data. It is particularly useful in fields like computer vision and NLP, where collecting labeled data is expensive and time-consuming.
Common Data Augmentation Techniques
-
Image Data Augmentation (Used in deep learning for computer vision tasks):

- Rotation: Rotating images by small degrees to simulate different perspectives.
- Cropping: Randomly cropping parts of the image to focus on different areas.
- Flipping: Horizontally or vertically flipping images.
- Scaling: Resizing images while maintaining aspect ratios.
- Brightness/Contrast Adjustments: Modifying brightness and contrast to simulate lighting variations.
- Noise Injection: Adding Gaussian noise to simulate different sensor conditions.
Example in TensorFlow/Keras:
from tensorflow.keras.preprocessing.image import ImageDataGenerator datagen = ImageDataGenerator( rotation_range=20, width_shift_range=0.1, height_shift_range=0.1, horizontal_flip=True, brightness_range=[0.8, 1.2] ) augmented_images = datagen.flow(x_train, y_train, batch_size=32) -
Text Data Augmentation (Used in NLP models):
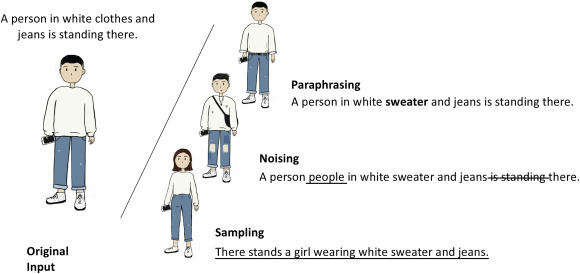
-
Synonym Replacement: Replacing words with their synonyms.
-
Random Insertion: Adding random words from the vocabulary.
-
Back Translation: Translating text to another language and back to introduce variation.
-
Sentence Shuffling: Reordering words or sentences slightly.
Example using
nlpaug:
import nlpaug.augmenter.word as naw aug = naw.SynonymAug(aug_src='wordnet') text = "Deep learning models require large amounts of data." augmented_text = aug.augment(text) print(augmented_text) -
-
Time-Series Data Augmentation (Used in financial data, speech processing):
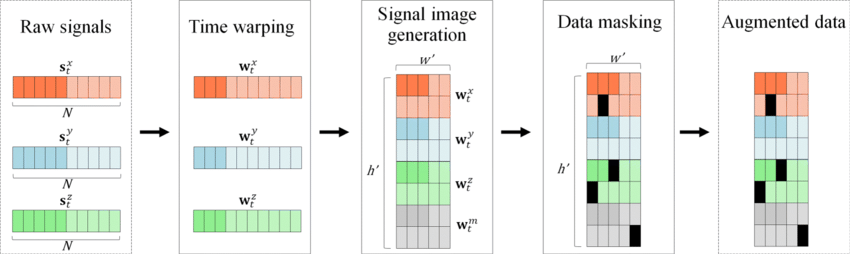
- Time Warping: Stretching or compressing time series data.
- Jittering: Adding small random noise to numerical values.
- Scaling: Multiplying data points by a random factor.
Data Synthesis
Data Synthesis involves generating entirely new data points that mimic real-world distributions. This is useful when real data is scarce or difficult to obtain.
Common Data Synthesis Techniques
-
Generative Adversarial Networks (GANs)
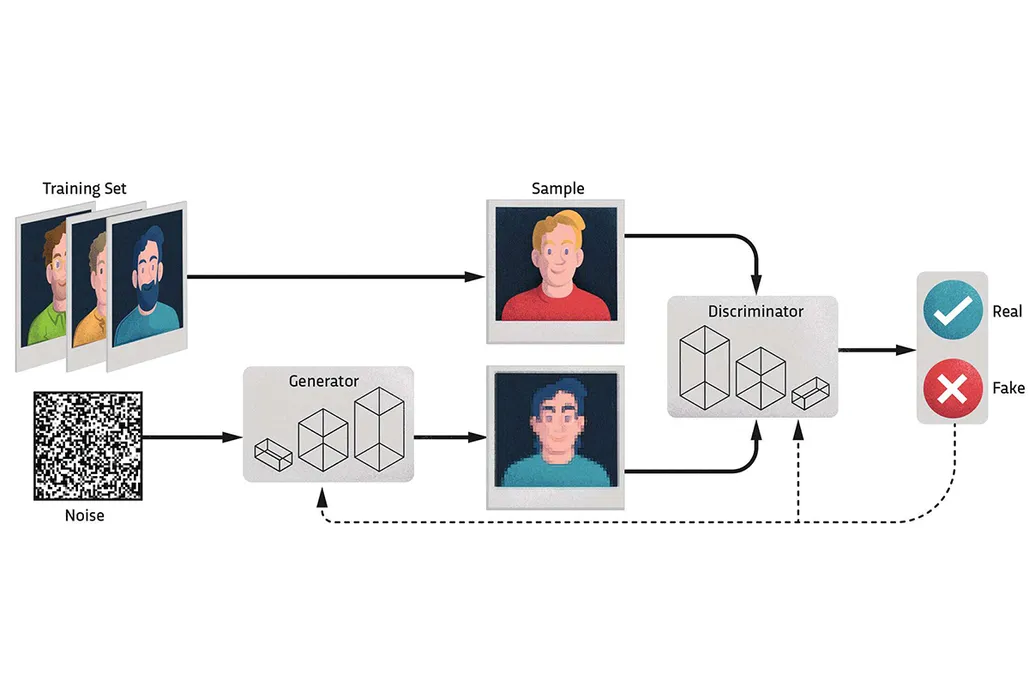
- GANs can generate realistic-looking images, text, or audio by learning the underlying distribution of the dataset.
- Example: GAN-generated human faces (thispersondoesnotexist.com).
Example GAN code using PyTorch:
import torch.nn as nn import torch.optim as optim class Generator(nn.Module): def __init__(self): super(Generator, self).__init__() self.fc = nn.Linear(100, 784) # 100-d noise vector to 28x28 image def forward(self, x): return torch.tanh(self.fc(x)) generator = Generator() noise = torch.randn(1, 100) fake_image = generator(noise) -
Bootstrapping
- A statistical method that resamples data with replacement to create new samples.
- Useful in small datasets to increase training size.
- Often used in ensemble learning (e.g., bagging).
-
Synthetic Minority Over-sampling (SMOTE)
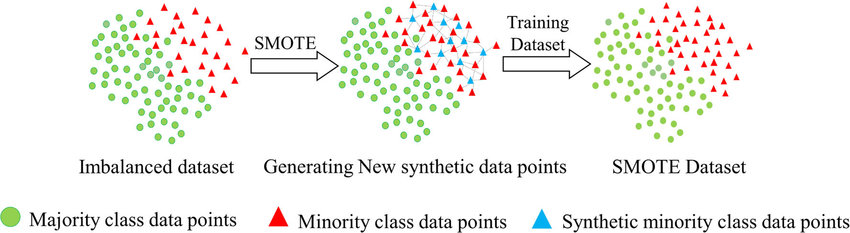
- Used in imbalanced datasets to generate synthetic minority class examples.
- Creates interpolated samples between existing data points.
- Example using
imbalanced-learn:
from imblearn.over_sampling import SMOTE from sklearn.model_selection import train_test_split X_resampled, y_resampled = SMOTE().fit_resample(X_train, y_train) -
Simulation-Based Synthesis
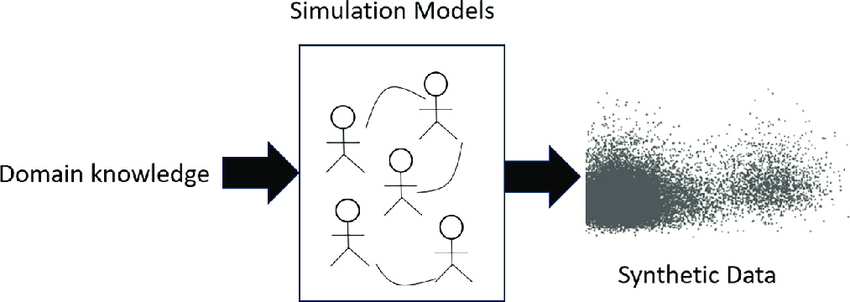
- Used in robotics, healthcare, and autonomous driving where real-world data collection is expensive or dangerous.
- Example: Self-driving cars trained on simulated environments before real-world deployment.
When to Use Data Augmentation vs. Data Synthesis?
| Method | Best for | Common Use Cases |
|---|---|---|
| Data Augmentation | Expanding existing datasets | Image classification, speech recognition |
| Data Synthesis | Creating new synthetic samples | GANs for image generation, NLP text synthesis |
Transfer Learning: Using Data from a Different Task
Transfer learning leverages pre-trained models:
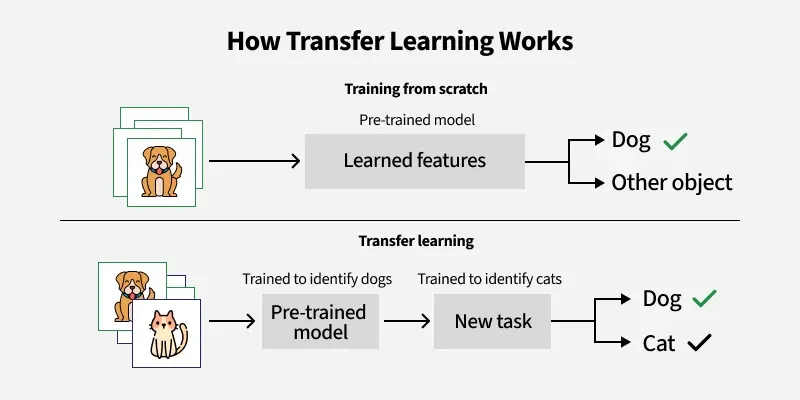
- Feature extraction: Use pre-trained model layers as feature extractors.
- Fine-tuning: Unfreeze layers and retrain on a new dataset.
Example: Using ImageNet-trained models for medical image classification.
Error Metrics for Skewed Datasets
In imbalanced datasets, accuracy alone is often misleading. For example, if a dataset has 95% negative samples and 5% positive samples, a model that always predicts "negative" will have 95% accuracy but is completely useless. Instead, we use more informative metrics:
Precision, Recall, and F1-Score
-
Precision (): Measures how many of the predicted positives are actually correct.
- High Precision: The model makes fewer false positive errors.
- Example: In an email spam filter, high precision means fewer legitimate emails are mistakenly classified as spam.
-
Recall (): Measures how many actual positives were correctly identified.
- High Recall: The model captures most of the actual positive cases.
- Example: In a medical test for cancer, high recall ensures that nearly all cancer cases are detected.
-
F1-Score: The harmonic mean of precision and recall, balancing both aspects.
- Used when both false positives and false negatives need to be minimized.
- F1-score ranges from 0 to 1, where 1 is the best possible score, indicating a perfect balance between precision and recall. However, what qualifies as a "good" or "bad" F1-score depends on the context of the problem.
Decision Trees
- Decision Tree Model
- Measuring Purity
- Choosing a Split: Information Gain
- Decision Trees for Continuous Features
- Regression Trees
- Using Multiple Decision Trees
Decision Tree Model
What is a Decision Tree?
A decision tree is a supervised machine learning algorithm used for classification and regression tasks. It mimics human decision-making by splitting data into branches based on feature values, forming a tree-like structure. The key components of a decision tree include:
- Root Node: The initial decision point that represents the entire dataset.
- Internal Nodes: Decision points where data is split based on a feature.
- Branches: The possible outcomes of a decision node.
- Leaf Nodes: The terminal nodes that provide the final classification or prediction.
graph TD;
Root[Root Node] -->|Feature 1| Node1[Node 1];
Root -->|Feature 2| Node2[Node 2];
Node1 --> Leaf1[Leaf Node 1];
Node1 --> Leaf2[Leaf Node 2];
Node2 --> Leaf3[Leaf Node 3];
Node2 --> Leaf4[Leaf Node 4];
Decision trees work by recursively splitting data based on a selected feature until a stopping condition is met.
Advantages and Disadvantages of Decision Trees
Advantages:
- Easy to Interpret: Decision trees provide an intuitive representation of decision-making.
- Handles Both Numerical and Categorical Data: They can work with mixed data types.
- No Need for Feature Scaling: Unlike algorithms like logistic regression or SVMs, decision trees do not require feature normalization.
- Works Well with Small Datasets: Decision trees can be effective even with limited data.
Disadvantages:
- Overfitting: Decision trees tend to learn patterns too specifically to the training data, leading to poor generalization.
- Sensitive to Noisy Data: Small variations in data can lead to different tree structures.
- Computational Complexity: For large datasets, training a deep tree can be time-consuming and memory-intensive.
Example: Classifying Fruits Using a Decision Tree
Consider a dataset containing different types of fruits characterized by their color, size, and texture. Our goal is to classify whether a given fruit is an apple or an orange.
| Color | Size | Texture | Fruit |
|---|---|---|---|
| Red | Small | Smooth | Apple |
| Green | Small | Smooth | Apple |
| Yellow | Large | Rough | Orange |
| Orange | Large | Rough | Orange |
Decision Tree Representation:
graph TD;
Root[Is Size Large?]
Root -- Yes --> Node1[Is Texture Rough?]
Root -- No --> Apple[Apple]
Node1 -- Yes --> Orange[Orange]
Node1 -- No --> Apple[Apple]
The decision tree follows a top-down approach:
- The root node first checks whether the fruit is large.
- If yes, it checks whether the texture is rough.
- If the texture is rough, it classifies the fruit as an orange; otherwise, it's an apple.
This example demonstrates how decision trees break down complex decision-making processes into simple binary decisions.
The learning process involves recursively splitting the dataset into smaller subsets. The splitting criterion is chosen based on purity measures such as Gini impurity or entropy. Each split creates child nodes until the stopping condition is met.
Stopping Criteria and Overfitting
A decision tree can continue growing until each leaf contains only one class. However, this often leads to overfitting, where the model memorizes the training data but fails to generalize to new data. To prevent this, stopping criteria such as:
- A minimum number of samples per leaf
- A maximum tree depth
- A minimum purity gain
can be used. Additionally, pruning techniques help reduce overfitting by removing branches that add little predictive value.
Pruning Example
- Pre-pruning: Stop the tree from growing beyond a certain depth.
- Post-pruning: Grow the full tree and then remove unimportant branches based on validation performance.
Measuring Purity
In decision trees, "purity" refers to how homogeneous the data in a given node is. A node is considered pure if it contains only samples from a single class. Measuring purity is essential for determining the best way to split a dataset to build an effective decision tree. The two most common metrics used for measuring purity are Entropy and Gini Impurity.
Entropy
Entropy, derived from information theory, measures the randomness or disorder in a dataset. The entropy equation for a binary classification problem is:
where:
- and are the proportions of each class in the set .
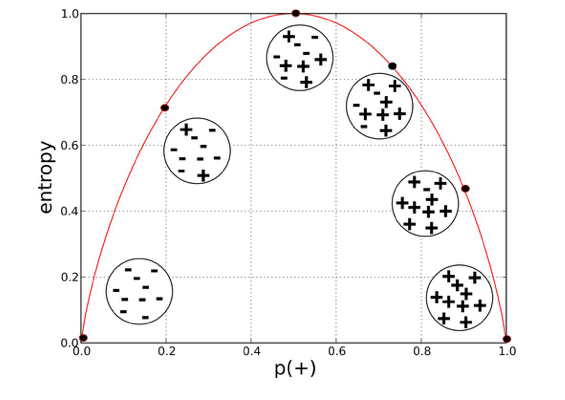
- Entropy = 0: The node is pure (all samples belong to one class).
- Entropy is high: The node contains a mix of different classes, meaning more disorder.
- Entropy is maximized at 0.5: If there is an equal probability of both classes (i.e., 50%-50%), the entropy is at its highest.
Example Calculation:
If a node contains 8 positive examples and 2 negative examples, the entropy is calculated as:
Gini Impurity
Gini Impurity measures how often a randomly chosen element from the set would be incorrectly classified if it were randomly labeled according to the class distribution.
The formula for Gini impurity is:
where:
- is the probability of class in the dataset.
graph TD;
A(Class Distribution) -->|Pure Node| B(Entropy = 0, Gini = 0);
A -->|50-50 Split| C(Entropy = 1, Gini = 0.5);
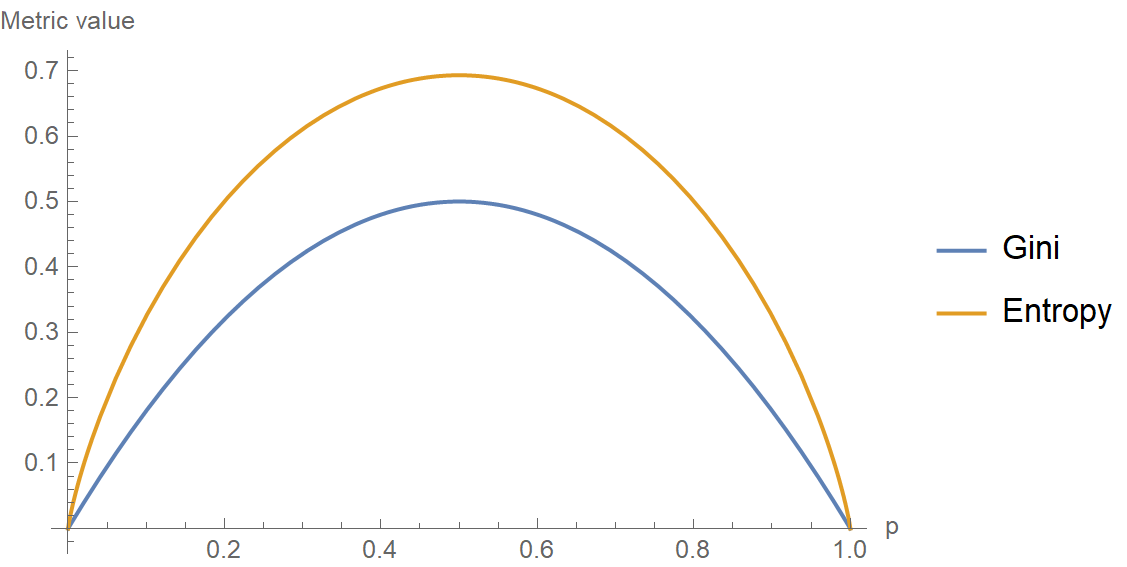
- Gini = 0: The node is completely pure.
- Gini is high: The node contains a mixture of classes.
Example Calculation:
For the same node with 8 positive and 2 negative examples:
Both metrics are used to determine the best way to split a node in a decision tree, but they have slight differences:
- Entropy is more computationally expensive since it involves logarithmic calculations.
- Gini Impurity is faster to compute and often preferred in decision tree implementations like CART (Classification and Regression Trees).
In practice, both perform similarly, and the choice depends on the specific problem and computational constraints.
By using these metrics, we can quantify the impurity of nodes and use them to decide the best possible splits while constructing a decision tree.
Choosing a Split: Information Gain
When constructing a decision tree, selecting the best feature to split on is crucial for building an optimal model. The goal is to maximize the Information Gain, which measures how well a feature separates the data into pure subsets.
Reducing Entropy
Information Gain (IG) is the reduction in entropy after splitting on a feature. It is calculated as:
where:
- is the entropy of the original set.
- represents subsets created by splitting on attribute .
- is the weighted proportion of samples in each subset.
Example Calculation
Consider a dataset with the following samples:
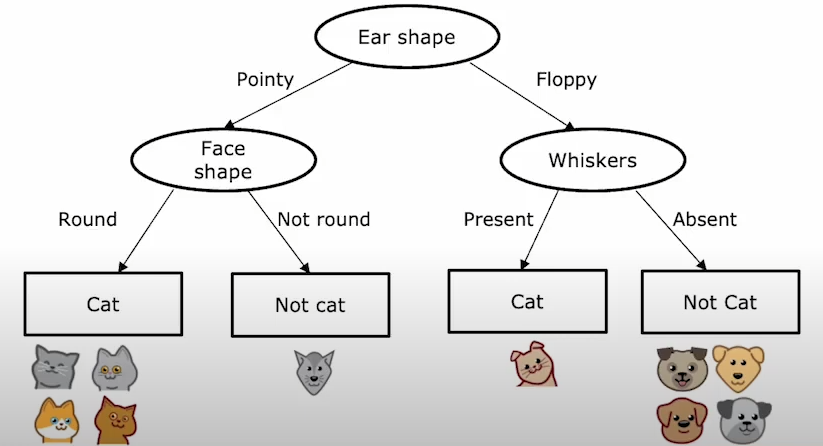
-
Compute initial entropy:
- 5
Catlabels and 5Doglabels.
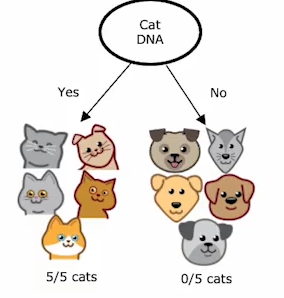
-
, .
-
.
- 5
-
Compute entropy after splitting by
Ear Shape:-
Subset
Pointy: {Cat, Cat, Cat, Cat, Dog} -
Subset
Floppy: {Cat, Dog, Dog, Dog, Dog} -
-
-
Compute entropy after splitting by
Face Shape:-
Subset
Round: {Cat, Cat, Cat, Dog, Dog, Dog, Cat} -
Subset
Not Round: {Cat, Dog, Dog} -
-
-
Compute entropy after splitting by
Whiskers:-
Subset
Present: {Cat, Cat, Cat, Dog} -
Subset
Absent: {Dog, Dog, Dog, Dog, Cat, Cat} -
-
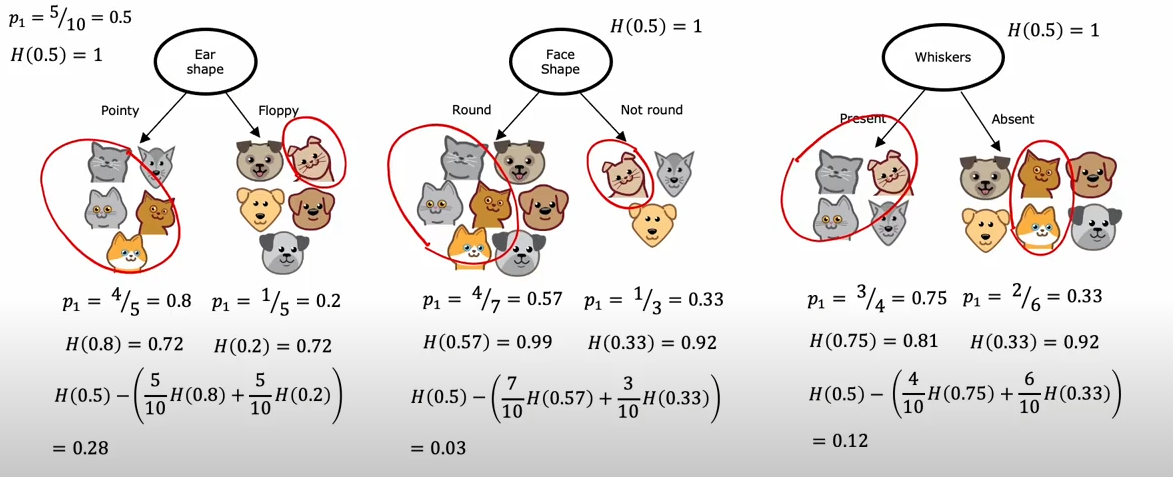
Since the highest Information Gain is (Ear Shape), splitting on either of these features is optimal.
Decision Trees for Continuous Features
When working with continuous features, decision trees can still be used effectively to predict outcomes, just like with categorical features.
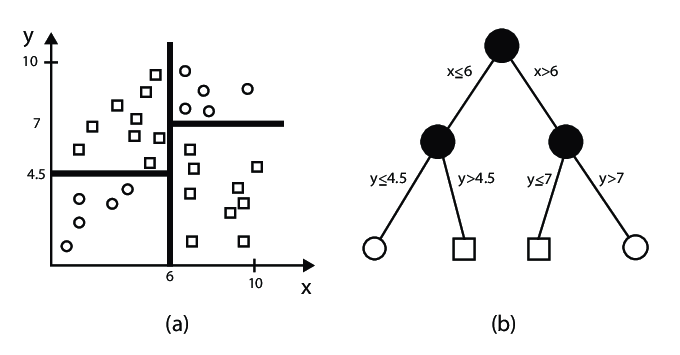
The key difference is that instead of using categorical values for splitting, decision trees for continuous features will determine optimal cutoffs or thresholds in the data. This allows the algorithm to make predictions for continuous target variables based on continuous input features.
In this example, we will predict whether an animal is a cat or dog based on its weight, using a decision tree that handles continuous features.
Let's say we have the following dataset of animals, and we want to predict if the animal is a cat or dog based on its weight:
| Animal | Weight (kg) |
|---|---|
| Cat | 4.5 |
| Cat | 5.1 |
| Cat | 4.7 |
| Dog | 8.2 |
| Dog | 9.0 |
| Cat | 5.3 |
| Dog | 10.1 |
| Dog | 11.4 |
| Dog | 12.0 |
| Dog | 9.8 |
Here, we aim to build a decision tree based on the Weight feature to determine whether an animal is a cat or a dog.
Step 1: Find the Best Split for the Weight Feature
We will evaluate potential splits based on the Weight feature. The decision tree will consider possible cutoffs and calculate the impurity or variance for each split.
Let's consider the following splits:
- Weight ≤ 7.0 kg: Assign
Cat - Weight > 7.0 kg: Assign
Dog
The decision tree will evaluate these splits by computing the impurity (for classification) or variance (for regression) for each possible split.
Step 2: Train a Decision Tree Model
We can use a decision tree to learn the best split and predict the animal type based on the weight. Here is how we can implement this in Python:
import numpy as np
from sklearn.tree import DecisionTreeClassifier
import pandas as pd
# Creating the dataset
data = {
'Weight': [4.5, 5.1, 4.7, 8.2, 9.0, 5.3, 10.1, 11.4, 12.0, 9.8],
'Animal': ['Cat', 'Cat', 'Cat', 'Dog', 'Dog', 'Cat', 'Dog', 'Dog', 'Dog', 'Dog']
}
df = pd.DataFrame(data)
# Splitting features and target
X = df[['Weight']] # Feature
y = df['Animal'] # Target
# Training a decision tree classifier
clf = DecisionTreeClassifier(criterion='gini', max_depth=1)
clf.fit(X, y)
# Predicting animal type
predictions = clf.predict(X)
print(f'Predicted Animals: {predictions}')
Step 3: Visualizing the Decision Tree
The decision tree can be visualized to show how the split is made based on the Weight feature.
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt
plt.figure(figsize=(10,8))
plot_tree(clf, feature_names=['Weight'], class_names=['Cat', 'Dog'], filled=True)
plt.show()
Step 4: Interpreting the Results
The resulting decision tree will have a root node where the Weight feature is split at a threshold (e.g., kg). If the animal's weight is less than or equal to kg, it is classified as a Cat; otherwise, it is classified as a Dog.
Regression Trees
Regression trees are used when the target variable is continuous rather than categorical. Unlike classification trees, which predict discrete labels, regression trees predict numerical values by recursively partitioning the data and assigning an average value to each leaf node.
How Regression Trees Work
- Splitting the Data: The algorithm finds the best feature and threshold to split the data by minimizing variance.
- Assigning Values to Leaves: Instead of class labels, leaf nodes store the mean of the target values in that region.
- Prediction: Given a new sample, traverse the tree based on feature values and return the mean value from the corresponding leaf node.
Example: Predicting Animal Weights
We extend our dataset by adding a new feature: Weight. Our dataset consists of 10 animals, with the following features:
- Ear Shape: (Pointy, Floppy)
- Face Shape: (Round, Not Round)
- Whiskers: (Present, Absent)
- Weight (kg): Continuous target variable
| Ear Shape | Face Shape | Whiskers | Animal | Weight (kg) |
|---|---|---|---|---|
| Pointy | Round | Present | Cat | 4.5 |
| Pointy | Round | Present | Cat | 5.1 |
| Pointy | Round | Absent | Cat | 4.7 |
| Pointy | Not Round | Present | Dog | 8.2 |
| Pointy | Not Round | Absent | Dog | 9.0 |
| Floppy | Round | Present | Cat | 5.3 |
| Floppy | Round | Absent | Dog | 10.1 |
| Floppy | Not Round | Present | Dog | 11.4 |
| Floppy | Not Round | Absent | Dog | 12.0 |
| Floppy | Round | Absent | Dog | 9.8 |
Building a Regression Tree
We use Mean Squared Error (MSE) to determine the best split. The split that results in the lowest MSE is selected.
Step 1: Compute Initial MSE
The overall mean weight is:
MSE before splitting:
Step 2: Find the Best Split
We evaluate splits based on feature values:
-
Split on Ear Shape:
- Pointy: → Mean =
- Floppy: → Mean =
- MSE = (better than initial MSE)
-
Split on Face Shape:
- Round: → Mean =
- Not Round: → Mean =
- MSE = (even better)
-
Split on Whiskers:
- Present: → Mean =
- Absent: → Mean =
- MSE = (better than initial but worse than Face Shape)
Thus, Face Shape is chosen as the first split.
Implementing in Python
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import pandas as pd
# Creating the dataset
data = {
'Ear_Shape': [0, 0, 0, 0, 0, 1, 1, 1, 1, 1], # 0: Pointy, 1: Floppy
'Face_Shape': [0, 0, 0, 1, 1, 0, 0, 1, 1, 0], # 0: Round, 1: Not Round
'Whiskers': [0, 0, 1, 0, 1, 0, 1, 1, 0, 0], # 0: Present, 1: Absent
'Weight': [4.5, 5.1, 4.7, 8.2, 9.0, 5.3, 10.1, 11.4, 12.0, 9.8]
}
df = pd.DataFrame(data)
# Splitting features and target
X = df[['Ear_Shape', 'Face_Shape', 'Whiskers']]
y = df['Weight']
# Training a regression tree
regressor = DecisionTreeRegressor(criterion='squared_error', max_depth=2)
regressor.fit(X, y)
# Predicting weights
predictions = regressor.predict(X)
print(f'Predicted Weights: {predictions}')
This regression tree provides predictions for the animal weights based on feature values.
Using Multiple Decision Trees
Using a single decision tree can sometimes lead to overfitting or instability, especially if the dataset has noise. By using multiple decision trees together, we can improve model performance and robustness. Two main techniques to achieve this are Bagging and Boosting.
Bagging (Bootstrap Aggregating)
Bagging reduces variance by training multiple decision trees on different random subsets of the dataset and then averaging their predictions. The most well-known example of bagging is the Random Forest algorithm.
Key Steps in Bagging:
- Draw random subsets (with replacement) from the training data.
- Train a decision tree on each subset.
- Combine predictions using majority voting (for classification) or averaging (for regression).
Visualization of Bagging:
graph TD;
A[Dataset] -->|Bootstrap Sampling| B1[Tree 1];
A[Dataset] -->|Bootstrap Sampling| B2[Tree 2];
A[Dataset] -->|Bootstrap Sampling| B3[Tree 3];
B1 --> C[Majority Vote];
B2 --> C;
B3 --> C;
Sampling with Replacement
Sampling with replacement is a technique where each data point has an equal probability of being selected multiple times in a new sample. This method is widely used in Bootstrap Aggregating (Bagging) to create multiple training datasets from the original dataset, allowing for robust model training and variance reduction.
- Why use Sampling with Replacement?
- It helps in reducing model variance.
- Generates multiple diverse datasets from the original dataset.
- Prevents overfitting by averaging multiple models.
Bootstrap Sampling Process
- Given a dataset of size , create a new dataset by randomly selecting samples with replacement.
- Some original samples may appear multiple times, while others may not appear at all.
- Train multiple models on these sampled datasets and aggregate predictions.
Consider a dataset with five samples :
| Original Data | Bootstrap Sample 1 | Bootstrap Sample 2 |
|---|---|---|
| A | B | A |
| B | A | C |
| C | C | A |
| D | D | B |
| E | A | E |
Notice that in each bootstrap sample, some samples appear multiple times while others are missing.
Random Forest Algorithm
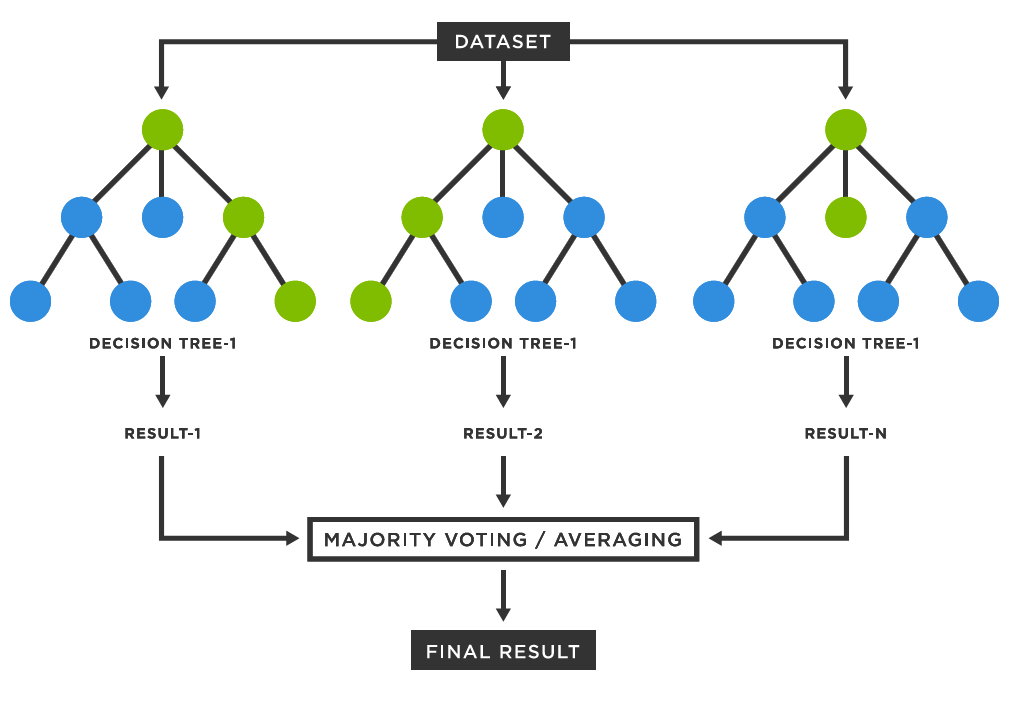
Random Forest is an ensemble learning method that builds multiple decision trees and merges them to achieve better performance. It is based on the concept of bagging (Bootstrap Aggregating), which helps reduce overfitting and improve accuracy.
How Random Forest Works
- Bootstrap Sampling: Randomly select subsets of the training data (with replacement).
- Decision Trees: Train multiple decision trees on different subsets.
- Feature Randomness: At each split, only a random subset of features is considered to introduce diversity.
- Aggregation:
- For classification, it takes a majority vote across all trees.
- For regression, it averages the predictions of all trees.
where is the number of trees and is the prediction of the tree.
Key Hyperparameters
| Hyperparameter | Description |
|---|---|
n_estimators | Number of decision trees in the forest |
max_depth | Maximum depth of each tree |
max_features | Number of features considered for splitting |
min_samples_split | Minimum samples required to split a node |
min_samples_leaf | Minimum samples required in a leaf node |
Decision Tree vs. Random Forest
graph TD;
A[Dataset] -->|Training| B[Single Decision Tree];
A -->|Bootstrap Sampling| C[Multiple Decision Trees];
C -->|Aggregation| D[Final Prediction];
Random Forest example on Telco Customer Churn Dataset
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, classification_report
# Load the dataset
df = pd.read_csv('Telco-Customer-Churn.csv')
# Preprocessing
df = df.drop(columns=['customerID']) # Remove non-relevant column
df = pd.get_dummies(df, drop_first=True) # Convert categorical variables
# Splitting data
X = df.drop(columns=['Churn_Yes'])
y = df['Churn_Yes']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Train Random Forest model
rf = RandomForestClassifier(n_estimators=100, max_depth=10, random_state=42)
rf.fit(X_train, y_train)
# Predictions
y_pred = rf.predict(X_test)
# Evaluation
print("Accuracy:", accuracy_score(y_test, y_pred))
print(classification_report(y_test, y_pred))
When to Use Random Forest
- When you need high accuracy with minimal tuning.
- When dealing with large feature spaces.
- When feature importance is important.
- When you want to reduce overfitting compared to decision trees.
Random Forest is a powerful and flexible model that performs well across various datasets. However, it can be computationally expensive for large datasets.
Boosting
Boosting is another ensemble method that builds trees sequentially, with each tree trying to correct the mistakes of the previous one. It focuses on difficult examples by assigning them higher weights.
The most popular boosting method is XGBoost (Extreme Gradient Boosting).
Key Steps in Boosting:
- Train a weak model on the training data.
- Identify misclassified samples and assign them higher weights.
- Train the next model focusing on these hard cases.
- Repeat until a stopping criterion is met.
Visualization of Boosting:
graph TD;
A[Dataset] -->|Train Weak Model| B1[Tree 1];
B1 -->|Adjust Weights| B2[Tree 2];
B2 -->|Adjust Weights| B3[Tree 3];
B3 --> C[Final Prediction];
XGBoost
XGBoost (Extreme Gradient Boosting) is a powerful and efficient implementation of gradient boosting that is widely used in machine learning competitions and real-world applications due to its high performance and scalability.
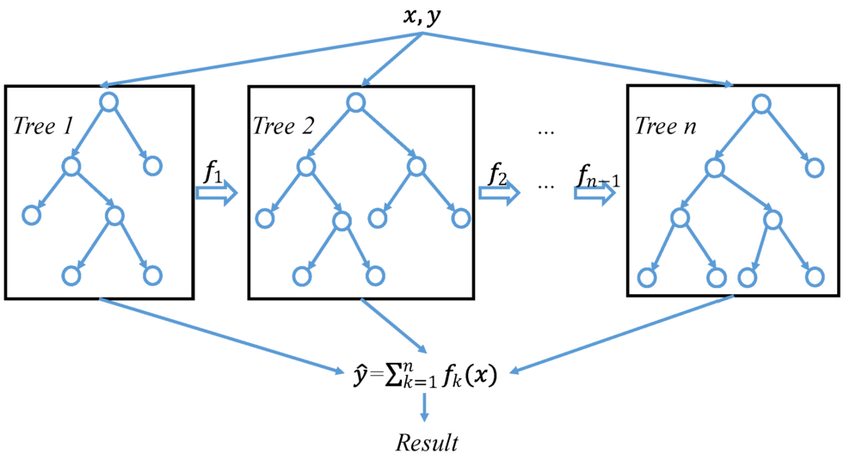
XGBoost builds an ensemble of decision trees sequentially, where each tree corrects the errors of the previous ones. The algorithm optimizes a loss function using gradient descent, allowing it to minimize errors effectively.
Key Components of XGBoost:
- Gradient Boosting Framework: Uses boosting to improve weak learners iteratively.
- Regularization: Includes L1 and L2 regularization to reduce overfitting.
- Parallelization: Optimized for fast training using parallel computing.
- Handling Missing Values: Automatically finds optimal splits for missing data.
- Tree Pruning: Uses depth-wise pruning instead of weight pruning for efficiency.
- Custom Objective Functions: Allows defining custom loss functions.
XGBoost optimizes the following objective function:
Where:
- is the loss function (e.g., squared error for regression, log loss for classification).
- is the regularization term controlling model complexity.
- represents individual trees.
Implementing XGBoost on Telco Customer Churn Dataset
We will train an XGBoost model to predict customer churn.
Step 1: Load the dataset
import pandas as pd
from xgboost import XGBClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# Load dataset
df = pd.read_csv("Telco-Customer-Churn.csv")
# Preprocess data
df = df.dropna()
df = pd.get_dummies(df, drop_first=True)
X = df.drop("Churn_Yes", axis=1)
y = df["Churn_Yes"]
# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
Step 2: Train the XGBoost Model
xgb_model = XGBClassifier(n_estimators=100, learning_rate=0.1, max_depth=4, reg_lambda=1, use_label_encoder=False, eval_metric='logloss')
xgb_model.fit(X_train, y_train)
Step 3: Evaluate the Model
y_pred = xgb_model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.4f}")
Hyperparameter Tuning
Key hyperparameters in XGBoost:
| Hyperparameter | Description |
|---|---|
n_estimators | Number of trees in the model. |
learning_rate | Step size for updating weights. |
max_depth | Maximum depth of trees. |
subsample | Fraction of samples used per tree. |
colsample_bytree | Fraction of features used per tree. |
gamma | Minimum loss reduction required for split. |
When to Use XGBoost
- When you have structured/tabular data.
- When you need high accuracy.
- When you need a model that handles missing values efficiently.
- When feature interactions are important.
XGBoost is one of the most powerful algorithms for predictive modeling. By leveraging its strengths in handling structured data, regularization, and parallel processing, it can significantly outperform traditional machine learning methods in many real-world applications.
XGBoost vs Random Forest
| Feature | XGBoost | Random Forest |
|---|---|---|
| Training Speed | Faster (parallelized) | Slower |
| Overfitting Control | Stronger (Regularization) | Moderate |
| Performance on Structured Data | High | Good |
| Handles Missing Data | Yes | No |
K-means Clustering
- What is Clustering?
- K-Means Intuition
- K-Means Algorithm
- Optimization Objective
- Initializing K-Means
- Choosing the Number of Clusters
- Implementation of K-Means in Python
- Choosing the Number of Clusters
- Advantages and Disadvantages of K-Means
- Conclusion
What is Clustering?
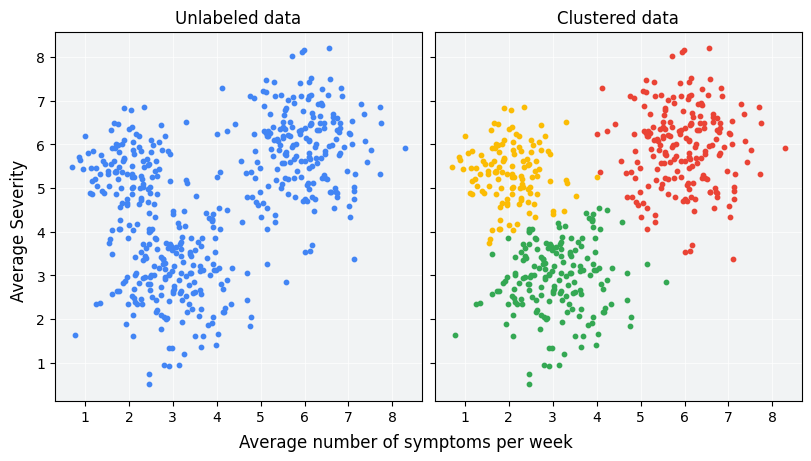
Clustering is an unsupervised learning technique used to group data points into distinct clusters based on their similarities. Unlike supervised learning, clustering does not rely on labeled data but instead identifies underlying structures within a dataset.
Applications of Clustering
- Customer Segmentation: Identifying groups of customers with similar purchasing behaviors.
- Anomaly Detection: Detecting fraudulent activities in financial transactions.
- Image Segmentation: Partitioning an image into meaningful regions.
- Document Categorization: Grouping documents with similar topics.
- Genomics: Identifying gene expression patterns and categorizing biological data.
- Social Network Analysis: Detecting communities within a network.
K-Means Intuition
K-Means is one of the most widely used clustering algorithms due to its simplicity, efficiency, and scalability. The primary goal of K-Means is to partition a given dataset into K clusters by minimizing intra-cluster variance while maximizing inter-cluster differences.
Key Intuition:
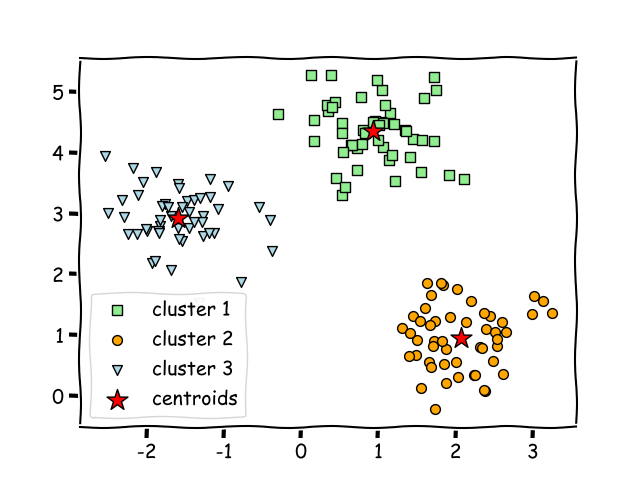
- Data points within the same cluster should be as similar as possible.
- Data points in different clusters should be as distinct as possible.
- The centroid of each cluster represents the
averageof all points in that cluster. - The algorithm iteratively improves the clusters until convergence.
K-Means Algorithm
The K-Means algorithm follows these steps:
- Initialize K cluster centroids randomly or using a specific method (e.g., K-Means++).
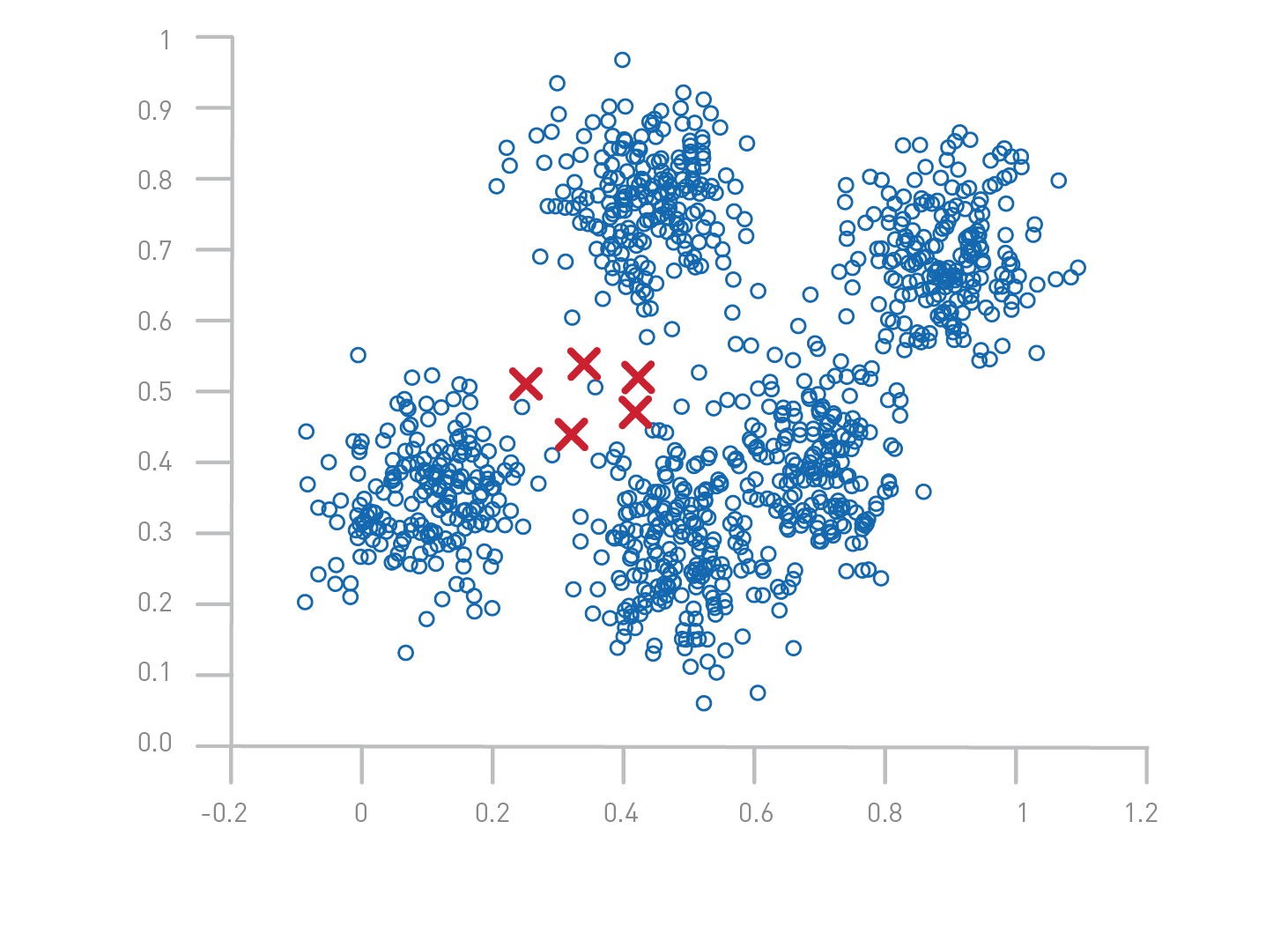
- Assign each data point to the nearest centroid using Euclidean distance:
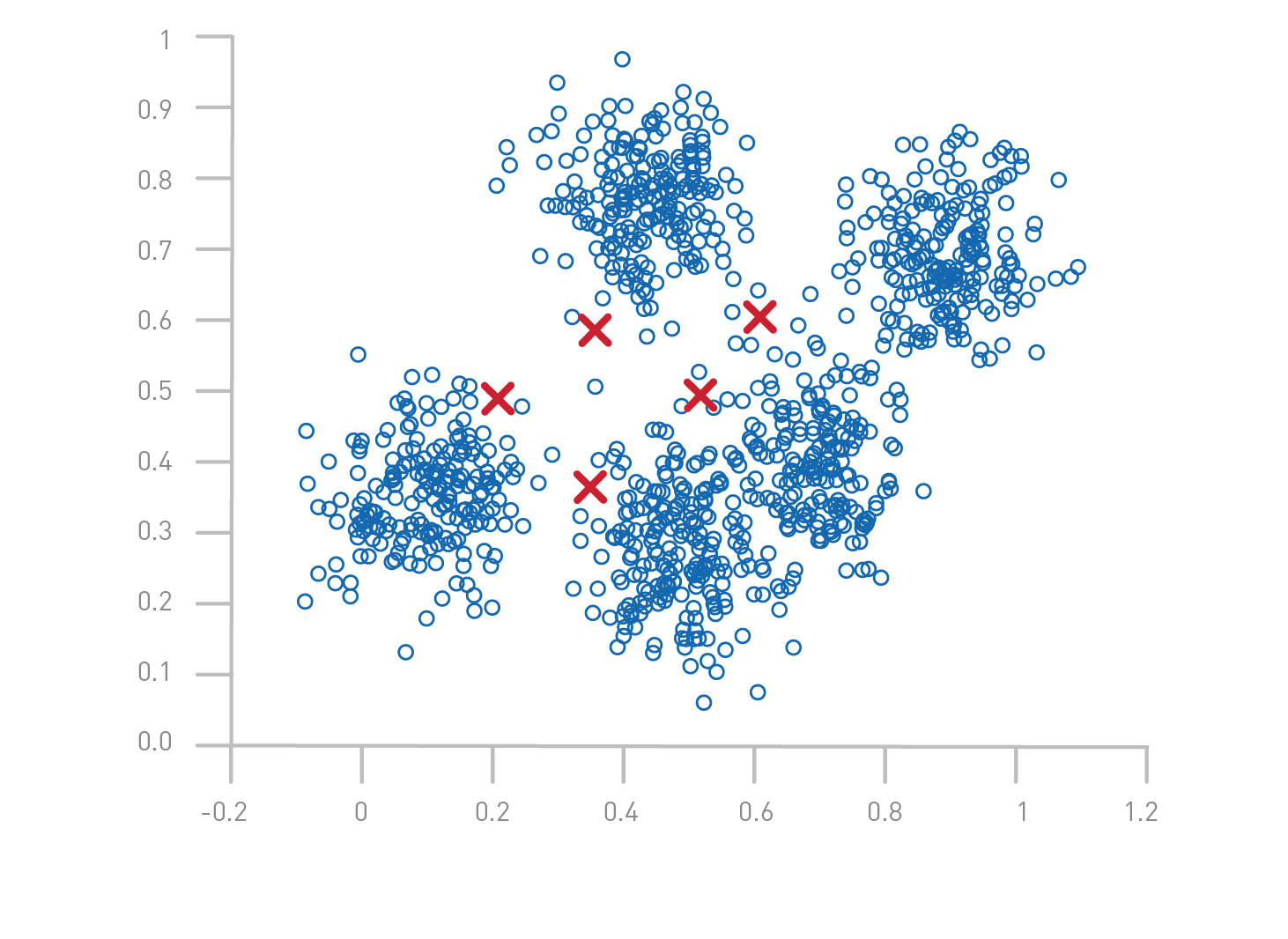
- Update centroids by computing the mean of all points assigned to each cluster:
where is the number of points in cluster .
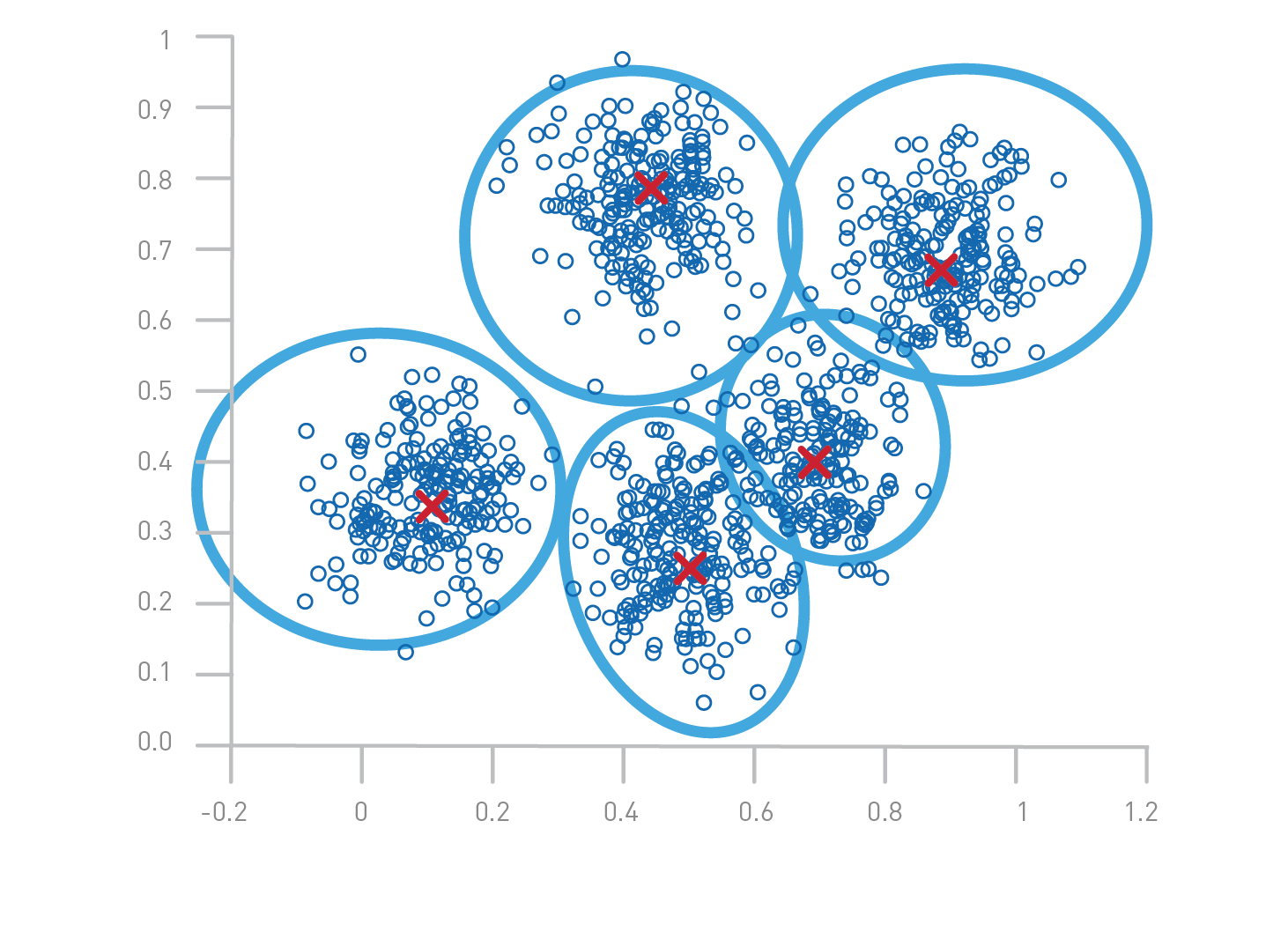
- Repeat until centroids stabilize (do not change significantly between iterations).
Optimization Objective
Consider data whose proximity measure is Euclidean distance. For our objective function, which measures the quality of a clustering, we use the sum of the squared error (SSE), which is also known as scatter.
In other words, we calculate the error of each data point, i.e., its Euclidean distance to the closest centroid, and then compute the total sum of the squared errors. Given two different sets of clusters that are produced by two different runs of K-means, we prefer the one with the smallest squared error, since this means that the prototypes (centroids) of this clustering are a better representation of the points in their cluster.
where:
- is a data point.
- is the centroid of cluster .
- is 1 if belongs to cluster , otherwise 0.
Initializing K-Means
Initialization significantly affects K-Means performance and results. Common initialization methods include:
- Random Initialization: Choosing K random points from the dataset.
- K-Means++ Initialization: A smarter method that spreads initial centroids to improve convergence speed and reduce the risk of poor clustering results.
- Forgy Method: Selecting K distinct data points as initial centroids.
Choosing the Number of Clusters
Selecting the appropriate number of clusters (K) is crucial. Common methods include:
- Elbow Method: Plotting WCSS vs. K and identifying the 'elbow' point.
- Silhouette Score: Measuring how similar a data point is to its own cluster vs. other clusters.
- Gap Statistic: Comparing WCSS against a random distribution to determine the optimal K.
Implementation of K-Means in Python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# Create a synthetic dataset
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=42)
# Apply K-Means
kmeans = KMeans(n_clusters=4, random_state=42)
kmeans.fit(X)
labels = kmeans.labels_
centroids = kmeans.cluster_centers_
# Plot the clusters
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', marker='o', edgecolor='black')
plt.scatter(centroids[:, 0], centroids[:, 1], s=200, c='red', marker='X')
plt.title("K-Means Clustering")
plt.show()
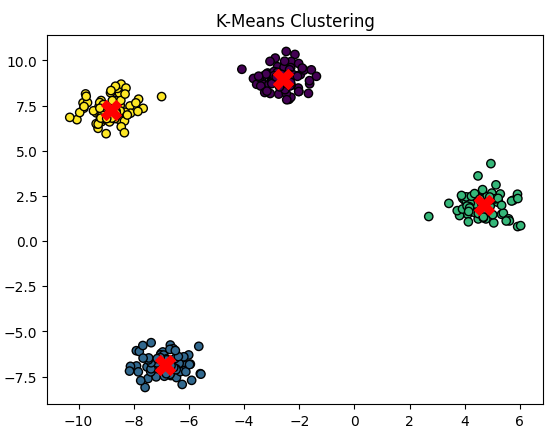
Choosing the Number of Clusters
Selecting the appropriate number of clusters (K) is crucial for obtaining meaningful results from K-Means clustering. Choosing too few clusters may result in underfitting, while choosing too many can lead to overfitting and unnecessary complexity. Several techniques help determine the optimal K:
1. Elbow Method
The Elbow Method is a widely used heuristic for selecting K by analyzing the Within-Cluster Sum of Squares (WCSS), also known as inertia.
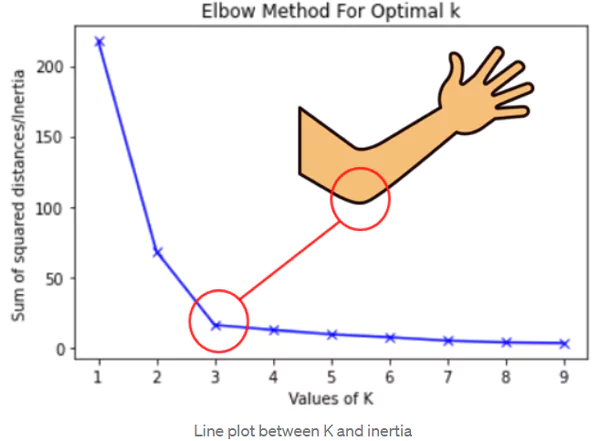
Steps:
- Run K-Means clustering for different values of K (e.g., from 1 to 10).
- Compute WCSS for each K. WCSS is defined as: where is the centroid of cluster and is a data point in that cluster.
- Plot WCSS vs. K and look for an 'elbow' point where the rate of decrease sharply changes.
- The optimal K is chosen at the elbow point, where adding more clusters does not significantly reduce WCSS.
2. Silhouette Score
The Silhouette Score measures how well-defined the clusters are by computing how similar a data point is to its own cluster compared to other clusters. It ranges from to :
- 1: Data point is well-clustered.
- 0: Data point is on the cluster boundary.
- -1: Data point is incorrectly clustered.
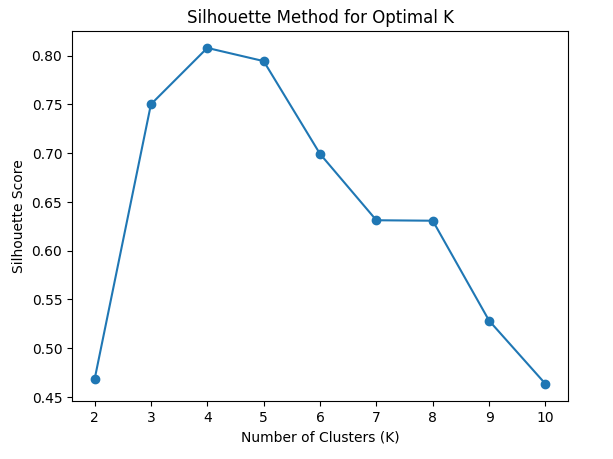
Steps:
- Compute the mean intra-cluster distance for each data point.
- Compute the mean nearest-cluster distance for each data point.
- Compute the silhouette score for each point:
- The overall Silhouette Score is the average of all .
- The optimal K is the one maximizing the Silhouette Score.
3. Gap Statistic
The Gap Statistic compares the clustering quality of the dataset against a random uniform distribution. It helps determine if a given clustering structure is significantly better than random clustering.
Steps:
- Run K-Means for different values of K and compute the within-cluster dispersion .
- Generate a random dataset with a similar range and compute .
- Compute the gap statistic: where is the number of random datasets.
- Choose the smallest K where is significantly large.
Advantages and Disadvantages of K-Means
Advantages
- Simplicity: Easy to understand and implement.
- Scalability: Efficient for large datasets.
- Fast Convergence: Typically converges in a few iterations.
- Works well for convex clusters: If clusters are well-separated, K-Means performs effectively.
- Interpretable Results: Clusters can be easily visualized and analyzed.
Disadvantages
- Choice of K: Requires prior knowledge or heuristic methods to select the number of clusters.
- Sensitivity to Initialization: Poor initial centroid selection can lead to suboptimal results.
- Not Suitable for Non-Convex Shapes: Struggles with arbitrarily shaped clusters.
- Affected by Outliers: Outliers can skew centroids, leading to poor clustering.
- Equal Variance Assumption: Assumes clusters have similar variance, which may not always hold.
Example of Poor Performance: If the dataset contains clusters with varying densities or non-spherical shapes, K-Means may misclassify data points. Alternatives like DBSCAN or Gaussian Mixture Models (GMMs) may perform better in such cases.
Conclusion
K-Means is a powerful clustering technique widely used across industries. While it is simple and efficient, it has limitations such as sensitivity to initialization and difficulty handling non-convex clusters. However, by applying optimization techniques and careful selection of K, it remains a strong tool in unsupervised learning.
Anomaly Detection
- Finding Unusual Events
- Gaussian (Normal) Distribution
- Anomaly Detection Algorithm
- Developing and Evaluating an Anomaly Detection System
- 5. Anomaly Detection vs. Supervised Learning
- Choosing What Features to Use
- Full Python Example with TensorFlow
Finding Unusual Events
Anomaly detection is the process of identifying rare or unusual patterns in data that do not conform to expected behavior. These anomalies may indicate critical situations such as fraud detection, system failures, or rare events in various fields like healthcare and finance.
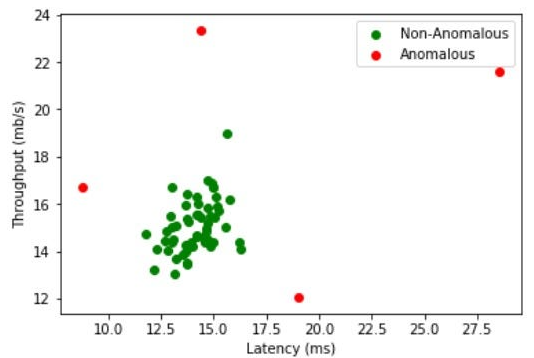
Real-World Examples
- Credit Card Fraud Detection: Identifying suspicious transactions that deviate significantly from a user’s normal spending habits.
- Manufacturing Defects: Detecting faulty products by identifying unusual patterns in production metrics.
- Network Intrusion Detection: Identifying cyber attacks by detecting unusual network traffic.
- Medical Diagnosis: Finding abnormal patterns in medical data that may indicate disease.
Gaussian (Normal) Distribution
The Gaussian distribution, also known as the normal distribution, is a fundamental probability distribution in statistics and machine learning. It is defined as:
Where:
- is the mean (expected value)
- is the variance
- is the variable of interest
Properties of Gaussian Distribution
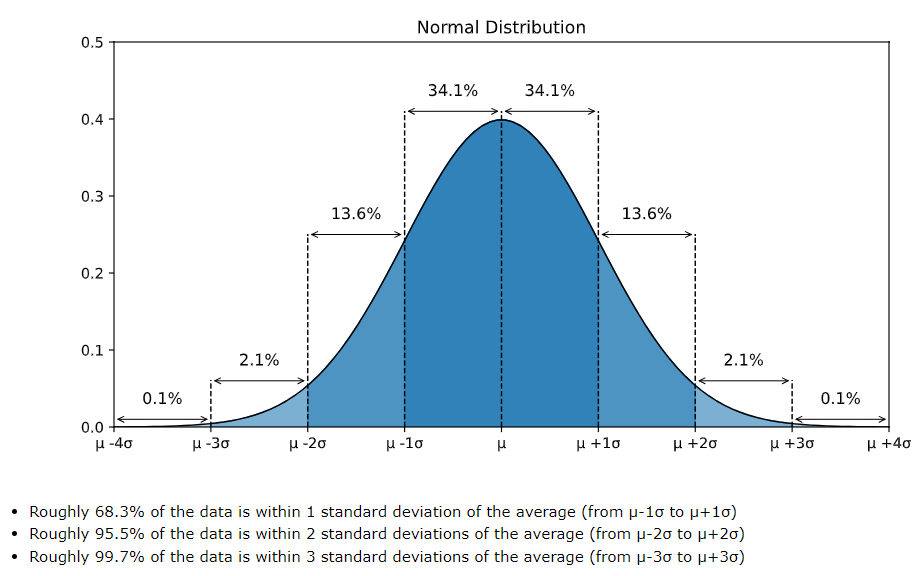
- Symmetric: Centered around the mean
- Rule:
- of values lie within standard deviation () of the mean.
- within standard deviations.
- within standard deviations.
Gaussian distribution is often used in anomaly detection to model normal behavior, where deviations from this distribution indicate anomalies.
Anomaly Detection Algorithm
Steps in Anomaly Detection
- Feature Selection: Identify relevant features from the dataset.
- Model Normal Behavior: Fit a probability distribution (e.g., Gaussian) to the normal data.
- Calculate Probability Density: Use the learned distribution to compute the probability density of new data points.
- Set a Threshold: Define a threshold below which data points are classified as anomalies.
- Detect Anomalies: Compare new observations against the threshold.
Mathematical Approach
For a feature , assuming a Gaussian distribution:
If is lower than a predefined threshold , then is considered an anomaly:
Developing and Evaluating an Anomaly Detection System
Data Preparation
- Obtain a labeled dataset with normal and anomalous instances
- Preprocess data: Handle missing values, normalize features
Model Training
- Estimate parameters and using training data:
- Compute probability density for test data
- Set anomaly threshold
Performance Evaluation
- Precision-Recall Tradeoff: Higher recall means catching more anomalies but may include false positives.
- F1 Score: Harmonic mean of precision and recall.
- ROC Curve: Evaluates different threshold settings.
5. Anomaly Detection vs. Supervised Learning
| Feature | Anomaly Detection | Supervised Learning |
|---|---|---|
| Labels Required? | No | Yes |
| Works with Unlabeled Data? | Yes | No |
| Suitable for Rare Events? | Yes | No |
| Examples | Fraud detection, Manufacturing defects | Spam detection, Image classification |
Choosing What Features to Use
- Domain Knowledge: Understand which features are relevant.
- Statistical Analysis: Use correlation matrices and distributions.
- Feature Scaling: Normalize or standardize data.
- Dimensionality Reduction: Use PCA or Autoencoders to reduce noise.
Full Python Example with TensorFlow
import numpy as np
import tensorflow as tf
from scipy.stats import norm
import matplotlib.pyplot as plt
# Generate synthetic normal data
np.random.seed(42)
data = np.random.normal(loc=50, scale=10, size=1000)
# Compute mean and variance
mu = np.mean(data)
sigma = np.std(data)
# Define probability density function
pdf = norm(mu, sigma).pdf(data)
# Set anomaly threshold (e.g., 0.001 percentile)
threshold = np.percentile(pdf, 1)
# Generate new test points
new_data = np.array([30, 50, 70, 100])
new_pdf = norm(mu, sigma).pdf(new_data)
# Detect anomalies
anomalies = new_data[new_pdf < threshold]
print("Anomalies detected:", anomalies)
# Plot
plt.figure(figsize=(10, 6))
plt.hist(data, bins=30, density=True, alpha=0.6, color='g')
x = np.linspace(min(data), max(data), 1000)
plt.plot(x, norm(mu, sigma).pdf(x), 'r', linewidth=2)
plt.scatter(anomalies, norm(mu, sigma).pdf(anomalies), color='red', marker='x', s=100, label='Anomalies')
plt.legend()
plt.show()
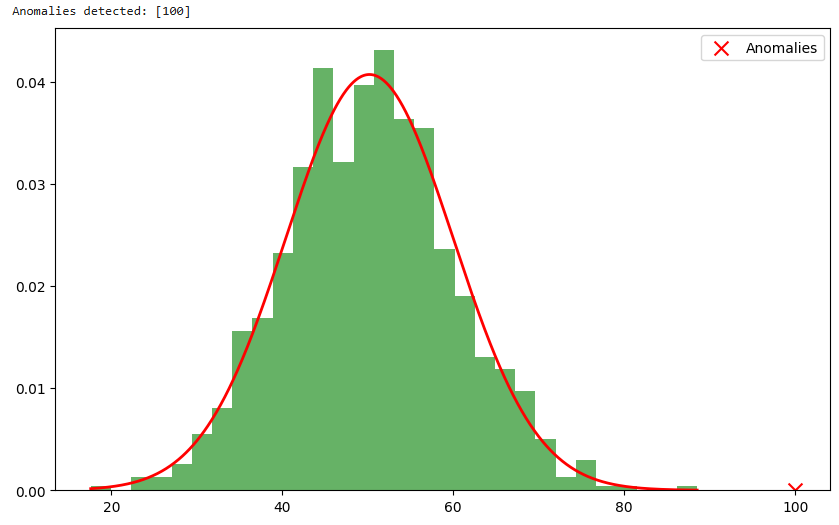
Explanation
- Generate synthetic data: We create a normal dataset.
- Compute mean and variance: Model normal behavior.
- Calculate probability density: Determine likelihood of each data point.
- Set threshold: Define an anomaly cutoff.
- Detect anomalies: Compare new observations against the threshold.
- Visualize results: Show normal distribution and detected anomalies.
This example provides a foundation for anomaly detection using probability distributions and can be extended with deep learning techniques like autoencoders or Gaussian Mixture Models (GMMs).
Recommender Systems
Recommender systems are everywhere in our digital lives, from Netflix suggesting movies based on our watch history to Amazon recommending products based on our previous purchases. These systems aim to predict what users might like based on their past behavior or the attributes of the items themselves.
Collaborative Filtering
Collaborative filtering is one of the most widely used techniques in recommender systems. It works by leveraging the behavior and preferences of users to make predictions about what they might like. Instead of relying on the characteristics of items themselves, collaborative filtering focuses on the interactions between users and items.
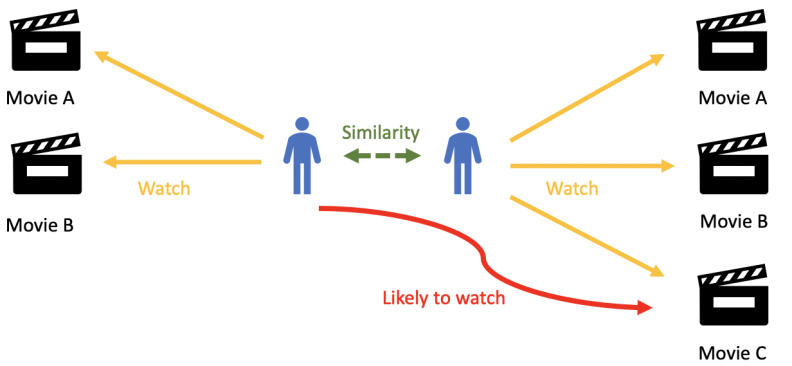
Imagine a streaming service like Netflix. If many users who watched "The Matrix" also watched "Inception," the system might recommend "Inception" to a user who has already watched "The Matrix." This works because the system assumes that similar users have similar tastes.
There are two main types of collaborative filtering:
- User-based Collaborative Filtering: Recommendations are made by finding users with similar preferences.
- Item-based Collaborative Filtering: Recommendations are made by finding similar items based on user interactions.
User-based Collaborative Filtering
Consider a movie recommendation system with four users (A, B, C, D) and seven movies (M1, M2, M3, M4, M5, M6, M7). The users have rated some of the movies on a scale from 1 to 5, but not every user has watched every movie. Our goal is to predict which unwatched movie user D would like the most and recommend it.
Below is the ratings matrix:
| User | M1 | M2 | M3 | M4 | M5 | M6 | M7 |
|---|---|---|---|---|---|---|---|
| A | 5 | 3 | 4 | - | 2 | - | 1 |
| B | 4 | - | 5 | 3 | 1 | 2 | - |
| C | 3 | 5 | - | 4 | - | 1 | 2 |
| D | - | 4 | 5 | 2 | 1 | - | - |
User D has not rated M1, M6, and M7, so we need to predict which one they are most likely to enjoy.
Finding Similar Users
We use a similarity measure to identify users most similar to D. A common choice is cosine similarity, defined as:
where:
- is the rating of user for item .
- is the set of items rated by both users.
Computing similarity between D and other users:
Using cosine similarity, we compare D with other users:
| User | M2 | M3 | M5 |
|---|---|---|---|
| A | 3 | 4 | 2 |
| D | 4 | 5 | 1 |
Similarly, we compute:
| User | M3 | M4 | M5 |
|---|---|---|---|
| B | 5 | 3 | 1 |
| D | 5 | 2 | 1 |
| User | M2 | M4 |
|---|---|---|
| C | 5 | 4 |
| D | 4 | 2 |
Since B is most similar to D, we estimate D's ratings for the unwatched movies (M1, M6, M7) using a weighted average:
Predicting Rating for M1
Using the weighted sum formula:
Repeating for M6 and M7, we get:
Since M1 has the highest predicted rating (3.998), we recommend M1 to user D.
- Predicted rating for M1: 3.998
- Predicted rating for M6: 1.494
- Predicted rating for M7: 1.505
Since M1 has the highest predicted rating, we recommend M1 to D.
Item-based Collaborative Filtering
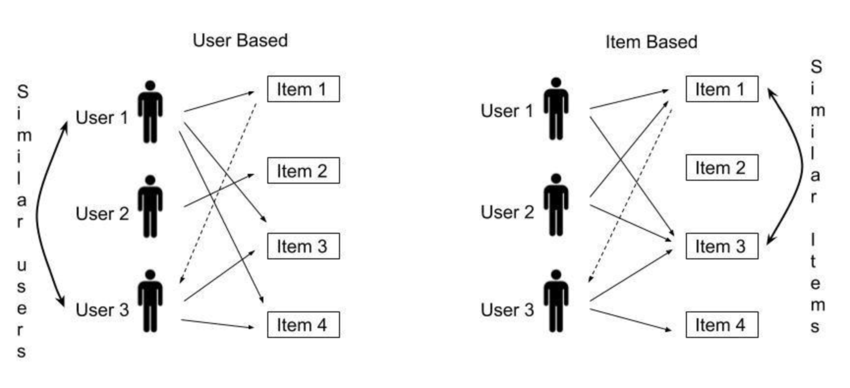
Rather than finding similar users, item-based collaborative filtering identifies similar items based on how users have rated them. The main idea is that if two movies are rated similarly by multiple users, they are likely to be similar.
Finding Similar Items
To determine item similarity, we use cosine similarity but compute it between movie rating vectors instead of user rating vectors.
Computing similarity between M1, M6, and M7 and other movies:
- sim(M1, M3) = 0.82
- sim(M6, M2) = 0.78
- sim(M7, M5) = 0.73
Since M3 is most similar to M1, we predict D's rating for M1 based on D's rating for M3:
After calculations:
- Predicted rating for M1: 4.1
- Predicted rating for M6: 3.7
- Predicted rating for M7: 3.6
Since M1 has the highest predicted rating, we again recommend M1 to D.
Conclusion
- User-based filtering finds similar users and recommends based on their preferences.
- Item-based filtering finds similar items and predicts ratings based on a user's history.
- Both methods predicted that D would like M1 the most, making it the best recommendation.
- These techniques can be combined for hybrid recommender systems to improve accuracy.
Content-Based Filtering
Content-based filtering recommends items to users by analyzing the characteristics of items a user has interacted with and comparing them with the characteristics of other items. Unlike collaborative filtering, which relies on user-item interactions, content-based filtering uses item metadata, such as genre, actors, or textual descriptions, to determine similarities.
Understanding Content-Based Filtering
In content-based filtering, each item is represented by a set of features. Users are assumed to have a preference for items with similar features to those they have previously liked. The recommendation process typically involves:

- Feature Representation: Representing items in terms of feature vectors.
- User Profile Construction: Creating a preference model for each user based on past interactions.
- Similarity Computation: Comparing new items with the user’s profile to generate recommendations.
- Generating Recommendations: Ranking items based on similarity scores and recommending the top ones.
To better understand this approach, let’s consider an example.
Example: Movie Recommendation
We have a dataset of seven movies, each described by three features: genre, director, and lead actor. Additionally, four users have rated some of these movies on a scale of 1 to 5.
Each movie is represented using a feature vector based on genre, director, and actors. We assign numerical values to categorical features using one-hot encoding.
| Movie | Action | Comedy | Drama | Sci-Fi | Director A | Director B | Actor X | Actor Y |
|---|---|---|---|---|---|---|---|---|
| M1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| M2 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| M3 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| M4 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| M5 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| M6 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| M7 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
User Ratings
| User | M1 | M2 | M3 | M4 | M5 | M6 | M7 |
|---|---|---|---|---|---|---|---|
| A | 5 | 3 | 4 | - | 2 | - | 1 |
| B | 4 | - | 5 | 3 | 1 | 2 | - |
| C | 3 | 5 | - | 4 | - | 1 | 2 |
| D | - | 4 | 5 | 2 | 1 | - | - |
Step 1: Constructing User Profiles
For each user, we compute a preference vector by averaging the feature vectors of the movies they have rated, weighted by their ratings.
For example, user D has rated three movies: M2 (4), M3 (5), and M4 (2). Their profile vector is computed as:
This results in a vector representing user D’s preferences.
Step 2: Computing Similarity Scores
To recommend a new movie (e.g., M6 or M7), we compute the cosine similarity between the user’s preference vector and the feature vector of the candidate movies:
Where is the dot product and and are the magnitudes.
Step 3: Generating Recommendations
By ranking the movies based on their similarity scores with the user’s profile, we can recommend the highest-ranked movie. If M6 has a similarity of 0.85 and M7 has 0.75, we recommend M6.
Advantages and Challenges of Content-Based Filtering
Advantages:
- Personalized recommendations based on individual preferences.
- Does not suffer from the cold start problem for items.
- No need for extensive user interaction data.
Challenges:
- Requires well-defined item features.
- Struggles with the cold start problem for new users.
- Limited to recommending items similar to those already interacted with.
By integrating deep learning techniques, such as word embeddings and neural networks, content-based filtering can improve accuracy and extend recommendations beyond direct similarities.
Principal Components Analysis (PCA)
Principal Components Analysis (PCA) is a dimensionality reduction technique used in machine learning and statistics to transform a large set of correlated features into a smaller set of uncorrelated features called principal components. This helps in reducing the complexity of data while retaining most of its variability.
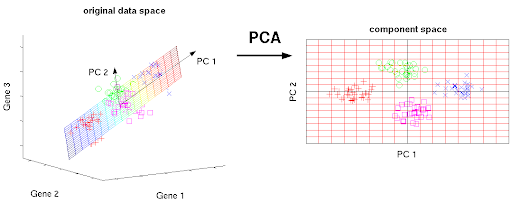
PCA is commonly used in:
- Reducing the number of features in high-dimensional datasets while preserving as much variance as possible.
- Visualizing high-dimensional data in 2D or 3D.
- Noise filtering and data compression.
- Feature extraction and selection.
Why PCA?
In many machine learning tasks, data often has a high number of dimensions, making computation expensive and difficult to interpret. For example, a movie recommender system might have thousands of features per movie (genre, director, actors, ratings, etc.). By using PCA, we can reduce this number to a smaller set of components that capture the most important patterns in the data.
How PCA Works
PCA involves the following steps:
- Standardization: The data is centered by subtracting the mean and scaled to have unit variance.
- Covariance Matrix Computation: A covariance matrix is computed to understand feature relationships.
- Eigenvalue and Eigenvector Computation: The eigenvalues and eigenvectors of the covariance matrix are found.
- Choosing Principal Components: The eigenvectors corresponding to the largest eigenvalues are selected as the principal components.
- Transforming the Data: The original data is projected onto the new principal component axes.
Mathematical Foundation of PCA
Step 1: Standardization
Since PCA relies on variance, the data should be standardized to have a mean of zero and unit variance:
where:
- is the original feature,
- is the mean of the feature,
- is the standard deviation.
Step 2: Compute the Covariance Matrix
The covariance matrix captures relationships between different features:
where is the standardized data matrix.
Step 3: Eigenvalues and Eigenvectors
PCA identifies principal components by computing eigenvalues and eigenvectors of the covariance matrix:
where:
- are eigenvalues (variance captured by each principal component),
- are eigenvectors (principal component directions).
Step 4: Project Data onto Principal Components
Data is transformed into the new coordinate system:
where contains the top eigenvectors.
PCA Visualization Example
We will visualize a dataset before and after applying PCA.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from mpl_toolkits.mplot3d import Axes3D
# 3D veriyi oluşturma
np.random.seed(42)
n_samples = 100
mean1 = [2, 2, 2]
cov1 = [[1, 0.5, 0.2], [0.5, 1, 0.1], [0.2, 0.1, 1]]
data1 = np.random.multivariate_normal(mean1, cov1, n_samples)
mean2 = [5, 5, 5]
cov2 = [[1, -0.3, 0.1], [-0.3, 1, -0.2], [0.1, -0.2, 1]]
data2 = np.random.multivariate_normal(mean2, cov2, n_samples)
X = np.concatenate((data1, data2))
y = np.concatenate((np.zeros(n_samples), np.ones(n_samples)))
# 3D veriyi görselleştirme
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(121, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap='coolwarm', edgecolors='k')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Original 3D Data')
# PCA uygulama
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# 2D veriyi görselleştirme
ax2 = fig.add_subplot(122)
ax2.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='coolwarm', edgecolors='k')
ax2.set_xlabel('Principal Component 1')
ax2.set_ylabel('Principal Component 2')
ax2.set_title('Data After PCA (2D)')
plt.tight_layout()
plt.show()
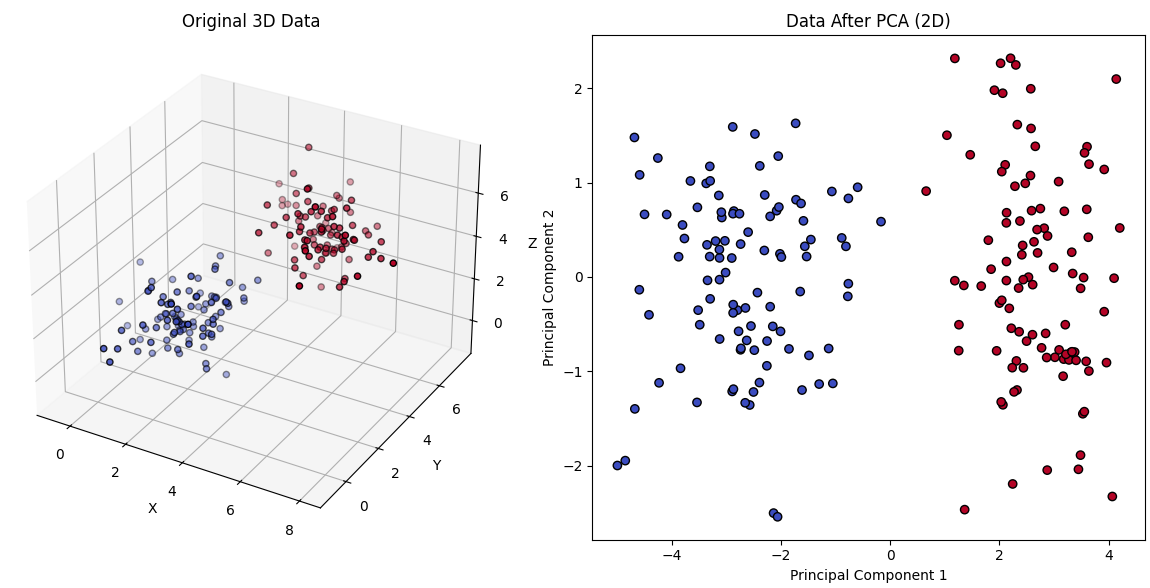
- The first plot shows the original dataset.
- The second plot shows the data projected onto the two principal components.
- PCA effectively captures the main variance in the data while reducing its dimensionality.
Conclusion
PCA is a fundamental technique for dimensionality reduction and data visualization. By identifying principal components, it helps uncover patterns, reduce noise, and improve machine learning model efficiency. However, PCA assumes linearity and may not perform well for highly non-linear data, where techniques like t-SNE or UMAP might be better alternatives.
Reinforcement Learning
- What is Reinforcement Learning?
- Markov Decision Process (MDP)
- State-Action Value Function ()
- Bellman Equation
- Stochastic Environment (Randomness in RL)
- Continuous State vs. Discrete State
- Lunar Lander Example
- -Greedy Policy
- Mini-Batch Learning in Reinforcement Learning
What is Reinforcement Learning?
Reinforcement Learning (RL) is a machine learning paradigm where an agent learns to make sequential decisions by interacting with an environment to maximize a cumulative reward. Unlike supervised learning, where labeled data is provided, RL relies on trial and error, receiving feedback in the form of rewards or penalties.
Key Characteristics of Reinforcement Learning:
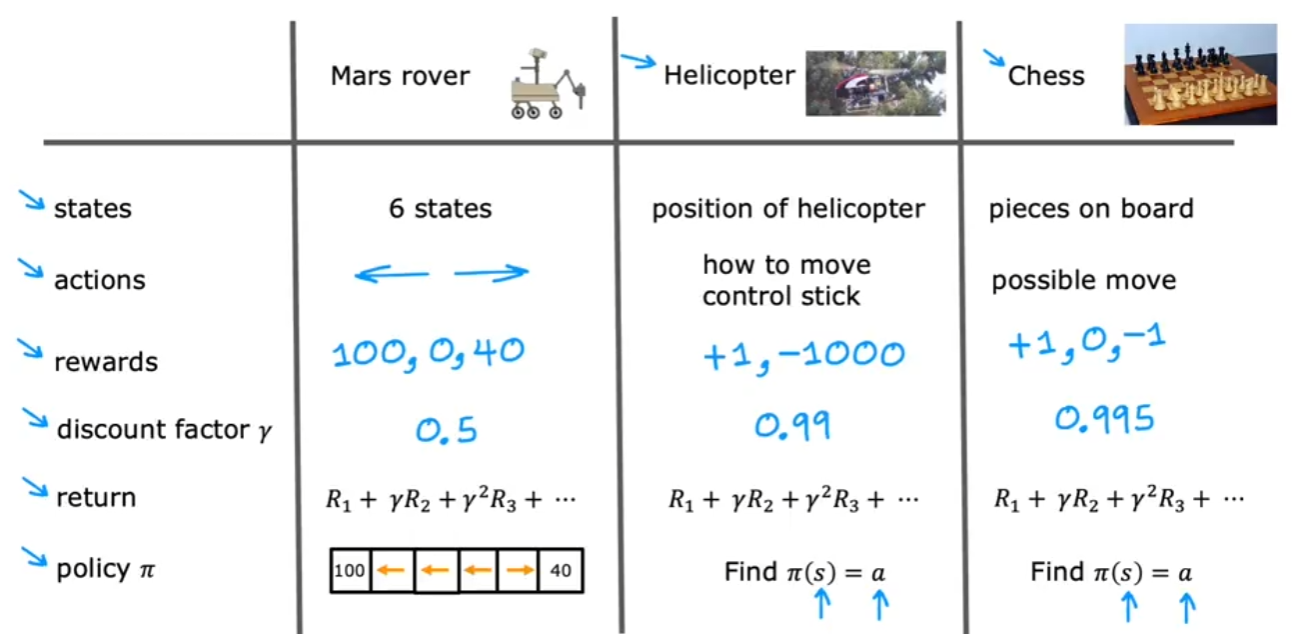
- Agent: The entity making decisions (e.g., a robot, a self-driving car, or an AI player in a game).
- Environment: The external system with which the agent interacts.
- State (s): A representation of the current situation of the agent in the environment.
- Action (a): A choice made by the agent at a given state.
- Reward (R): A numerical value given to the agent as feedback for its actions.
- Policy ( ): A strategy that maps states to actions.
- Return (G): The cumulative reward collected over time.
- Discount Factor ( ): A value between 0 and 1 that determines the importance of future rewards.
Mars Rover Example
Let's illustrate RL concepts using a Mars Rover example. Imagine a rover exploring a 1D terrain with six grid positions:
Each position is numbered from 1 to 6. The rover starts at position 4, and it can move left (-1) or right (+1). The goal is to maximize its rewards, which are given at positions 1 and 6:
- Position 1 reward: 100 (e.g., a research station with supplies)
- Position 6 reward: 40 (e.g., a safe resting point)
- Other positions reward: 0
States, Actions, and Rewards
| State | Possible Actions | Reward |
|---|---|---|
| 1 | Move right (+1) | 100 |
| 2 | Move left (-1), Move right (+1) | 0 |
| 3 | Move left (-1), Move right (+1) | 0 |
| 4 (Start) | Move left (-1), Move right (+1) | 0 |
| 5 | Move left (-1), Move right (+1) | 0 |
| 6 | Move left (-1) | 40 |
- The agent (rover) must decide which direction to move.
- The state is the current position of the rover.
- The action is moving left or right.
- The reward depends on reaching the goal states (1 or 6).
How the Rover Decides Where to Go
The rover's decision is based on maximizing its expected future rewards. Since it has two possible goal positions (1 and 6), it must evaluate different strategies. The rover should consider the following:
-
Immediate Reward Strategy
- If the rover focuses only on immediate rewards, it will move randomly, as most positions (except 1 and 6) have a reward of 0.
- This strategy is not optimal because it doesn't take future rewards into account.
-
Short-Term Greedy Strategy
- If the rover chooses the nearest reward, it will likely go to position 6 since it's closer than position 1.
- However, this might not be the best long-term decision.
-
Long-Term Reward Maximization
- The rover must evaluate how much discounted future reward it can accumulate.
- Even though position 6 has a reward of 40, position 1 has a much higher reward (100).
- If the rover can reliably reach position 1, it should favor this route, even if it takes more steps.
To formalize this, the rover can compute the expected return G for each possible path, considering the discount factor ().
Discount Factor () and Expected Return
The discount factor determines how much future rewards are valued relative to immediate rewards. If , all future rewards are considered equally important. If , future rewards are slightly less important than immediate rewards.
For example, if the rover follows a path where it expects to reach position 1 in 3 steps and receive 100 reward, the discounted return is:
If it reaches position 6 in 2 steps and receives 40 reward, the return is:
Since 72.9 is greater than 32.4, the rover should prioritize going to position 1, even though it is farther away.
Policy ()
A policy () defines the strategy of the rover: for each state, it dictates which action to take. Possible policies include:
- Greedy policy: Always moves towards the highest reward state immediately.
- Exploratory policy: Sometimes tries new actions to find better strategies.
- Discounted return policy: Balances short-term and long-term rewards.
If the rover follows an optimal policy, it should compute the total expected reward for every possible action and pick the one that maximizes its long-term return.
Markov Decision Process (MDP)
Reinforcement Learning problems are often modeled as Markov Decision Processes (MDPs), which are defined by:
- Set of States (S):
- Set of Actions (A):
- Transition Probability (P): Probability of moving from one state to another given an action
- Reward Function (R): Defines the reward received when moving from to
- Discount Factor (): Determines the importance of future rewards.
In our Mars Rover example:
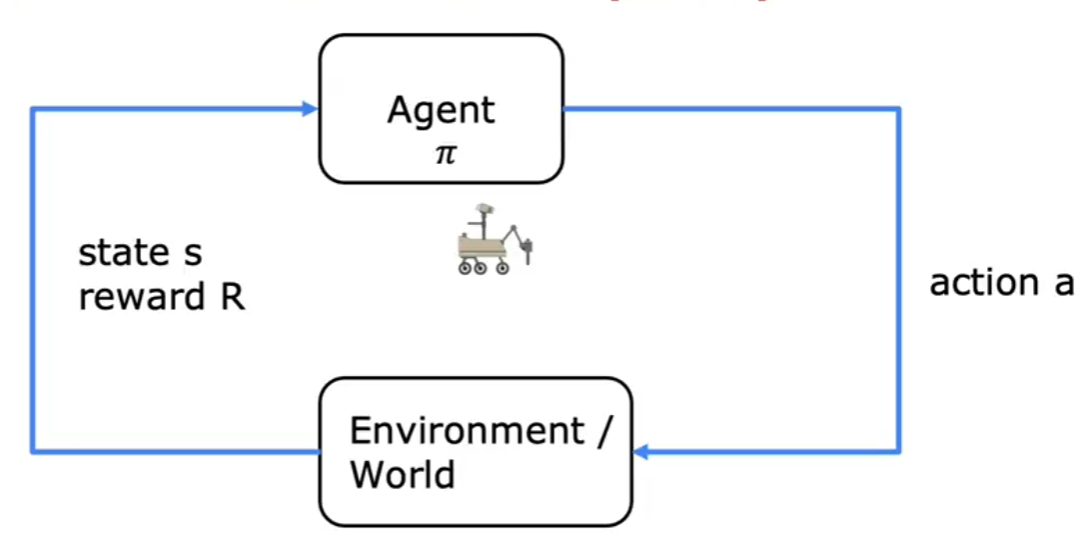
- States (S): {1, 2, 3, 4, 5, 6}
- Actions (A): {Left (-1), Right (+1)}
- Transition Probabilities (P): Deterministic (e.g., if the rover moves right, it always reaches the next state)
- Reward Function (R):
- , ,
- Discount Factor (): (assumed)
State-Action Value Function ()
The State-Action Value Function, denoted as , represents the expected return when starting from state , taking action , and then following a policy . Formally:
This function helps the agent determine which action will lead to the highest reward in a given state.
Applying to Mars Rover
Using our Mars rover example, we can estimate values for each state-action pair. Suppose:
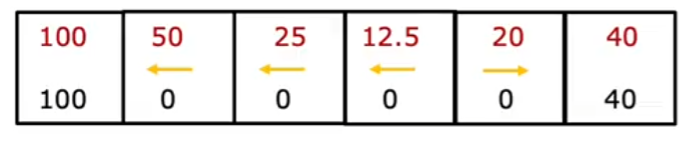
The rover should always select the action with the highest value to maximize rewards.
Bellman Equation
The Bellman Equation provides a recursive relationship for computing value functions in reinforcement learning. It expresses the value of a state in terms of the values of successor states.
Understanding the Bellman Equation
In reinforcement learning, an agent makes decisions in a way that maximizes future rewards. However, since future rewards are uncertain, we need a way to estimate them efficiently. The Bellman equation helps us do this by breaking down the value of a state into two components:
- Immediate Reward (): The reward received by taking action in state .
- Future Rewards (): The expected value of the next state , weighted by the probability of reaching that state.
The Bellman equation is written as:
where:
- : The value of state .
- : The immediate reward for taking action in state .
- : The discount factor (), which determines how much future rewards are considered.
- : The probability of reaching state after taking action .
- : The value of the next state .
Example Calculation for Mars Rover
Let’s assume:
- Moving from
4to3has a reward of-1. - Moving from
4to5has a reward of-1. - Position
1has a reward of100.
For :
If we assume and , and a discount factor , we compute:
Thus, the optimal value for state 4 is 44, meaning the agent should prefer moving left toward 3.
Intuition Behind the Bellman Equation
- The Bellman equation decomposes the value of a state into its immediate reward and the expected future reward.
- It allows us to compute values iteratively: we start with rough estimates and refine them over time.
- It helps in policy evaluation—determining how good a given policy is.
- It forms the foundation for Dynamic Programming methods like Value Iteration and Policy Iteration.
Stochastic Environment (Randomness in RL)
In real-world applications, environments are often stochastic, meaning actions do not always lead to the same outcome.
Stochasticity in the Mars Rover Example
Suppose the Mars rover’s motors sometimes malfunction, causing it to move in the opposite direction with a small probability (e.g., 10% of the time). Now, the transition dynamics include:
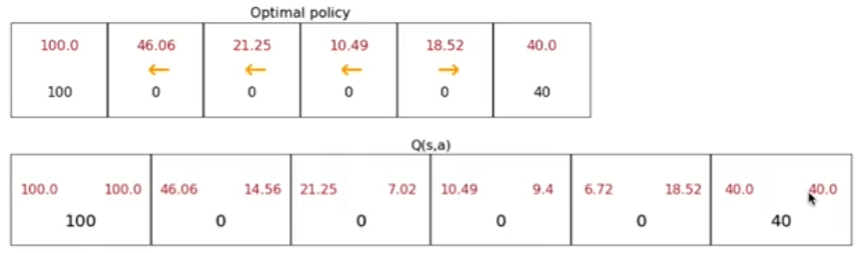
This randomness makes decision-making more challenging. Instead of just considering rewards, the rover must now account for expected rewards and the probability of ending up in different states.
Impact on Decision-Making
With stochastic environments, deterministic policies (always taking the best action) may not be optimal. Instead, an exploration-exploitation balance is needed:
- Exploitation: Following the best-known action based on past experience.
- Exploration: Trying new actions to discover potentially better rewards.
This concept is central to algorithms like Q-Learning and Policy Gradient Methods, which we will discuss in future sections.
Continuous State vs. Discrete State
In reinforcement learning, states can be either discrete or continuous. A discrete state means that the number of possible states is finite and well-defined, whereas a continuous state implies an infinite number of possible states.
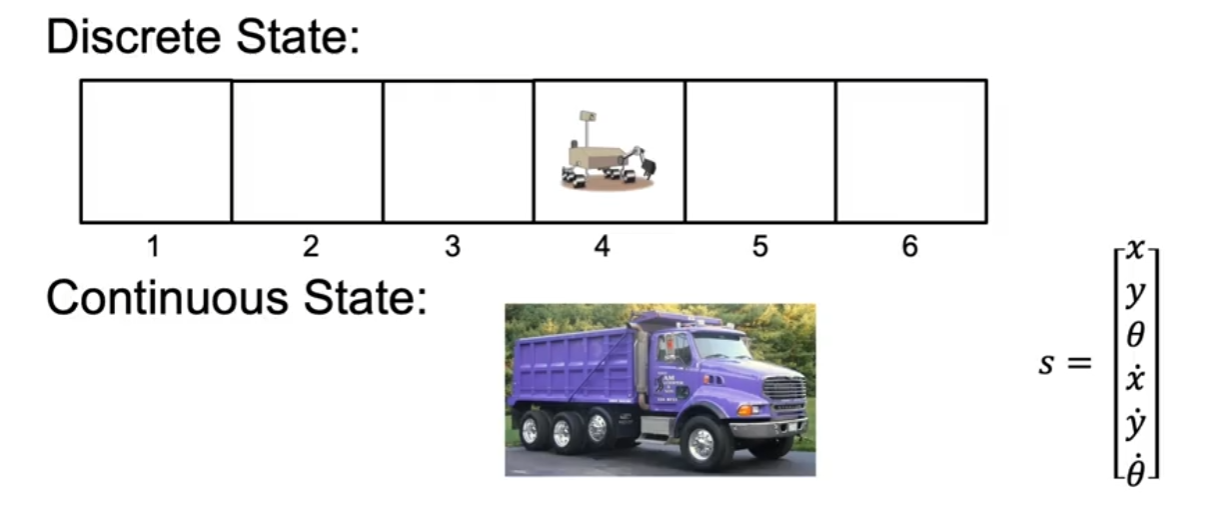
For example, consider our Mars Rover example with six possible states. The rover can be in any one of these six states at any given time, making it a discrete state environment. However, if we consider a truck driving on a highway, its position, speed, angle, and other attributes can take an infinite number of values, making it a continuous state environment.
Continuous state spaces are often approximated using function approximators like neural networks to generalize over an infinite number of states efficiently.
Lunar Lander Example
A classic reinforcement learning problem is the Lunar Lander, where the objective is to safely land a spacecraft on the surface of a planet. The agent (lander) interacts with the environment by selecting one of four possible actions:
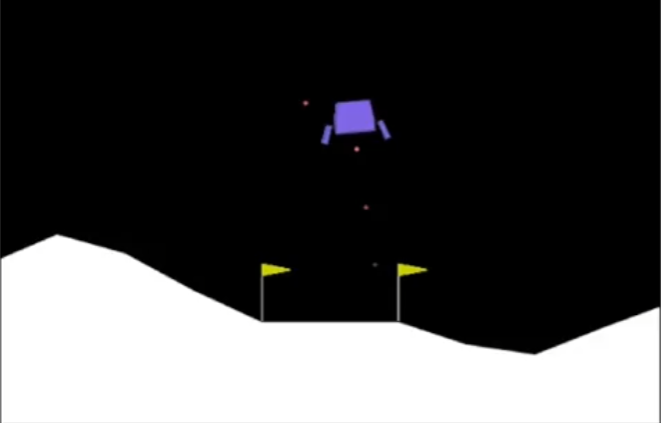
- Do Nothing: No thrust is applied.
- Left Thruster: Applies force to move left.
- Right Thruster: Applies force to move right.
- Main Thruster: Applies force to slow descent.
Rewards and Penalties:
The environment provides feedback through rewards and penalties:
- Soft Landing: +100 reward
- Crash Landing: -100 penalty
- Firing Main Engine: -0.3 penalty (fuel consumption)
- Firing Side Thrusters: -0.1 penalty (fuel consumption)
State Representation
The state of the lunar lander can be represented as:
where:
- : Position of the lander
- : Orientation (tilt angle)
- : Contact with left and right landing pads (binary values)
- : Velocities in x and y directions
- : Angular velocity
The policy function determines which action to take given the current state.
Deep Q-Network (DQN) Neural Network for Lunar Lander
To approximate the optimal policy, we use a deep neural network. The network takes the 8-dimensional state vector as input and predicts Q-values for each of the four actions.
Network Architecture:
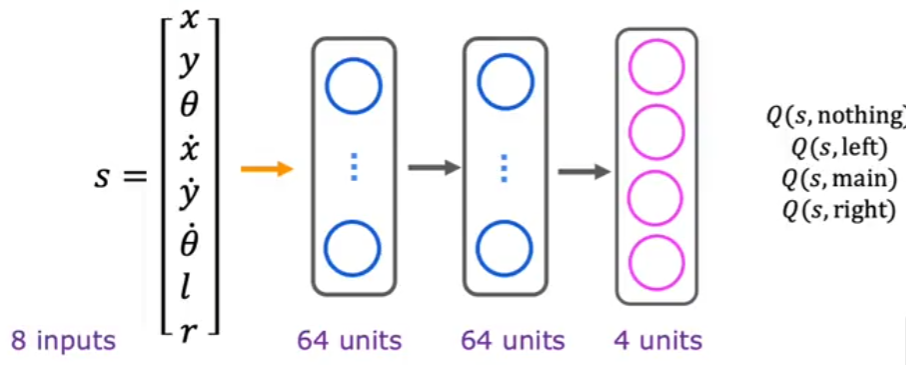
- Input Layer (8 neurons): Corresponds to
- Two Hidden Layers (64 neurons each, ReLU activation)
- Output Layer (4 neurons): Represents the Q-values for the four possible actions
The output neurons correspond to:
The network is trained using the Bellman equation to minimize the difference between predicted and actual Q-values.
-Greedy Policy
In reinforcement learning, an agent must balance exploration (trying new actions) and exploitation (choosing the best-known action). The -greedy policy is a common approach to achieve this balance:
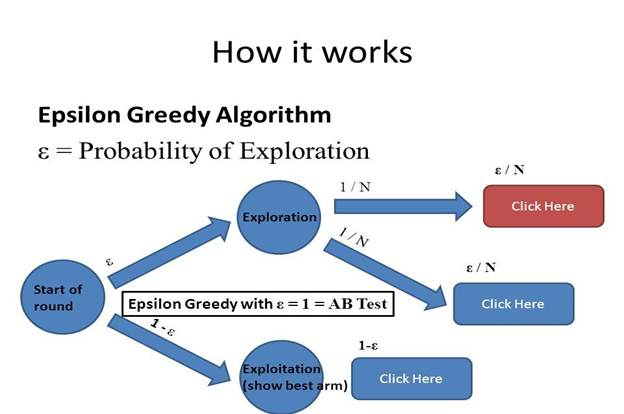
- With probability , take a random action (exploration).
- With probability , take the action with the highest Q-value (exploitation).
Initially, is set to a high value (e.g., 1.0) to encourage exploration and gradually decays over time.
Mini-Batch Learning in Reinforcement Learning
In deep reinforcement learning, we use mini-batch learning to improve training efficiency and stability.
Why Mini-Batch Learning?
- Prevents large updates from a single experience (stabilizes training).
- Helps break the correlation between consecutive experiences (improves generalization).
- Allows efficient GPU computation (faster convergence).
How It Works:
- Store experiences (state, action, reward, next state) in a replay buffer.
- Sample a mini-batch of experiences.
- Compute target Q-values using the Bellman equation.
- Perform a gradient descent update on the Q-network.
Mini-batch learning makes reinforcement learning more robust and prevents overfitting to recent experiences.
Welcome to Deep Learning notes.
∴
I completed the Deep Learning Specialization Course by taking detailed notes and summarizing critical concepts for future reference.
University of Stanford & DeepLearning.AI
— emreaslan —
Computer Vision and Edge Detection
- Computer Vision
- Edge Detection
Computer Vision
Introduction to Computer Vision
Computer Vision is a field of artificial intelligence (AI) that enables machines to interpret and understand visual information from the world. It encompasses tasks such as image recognition, object detection, and segmentation.
Real-World Applications
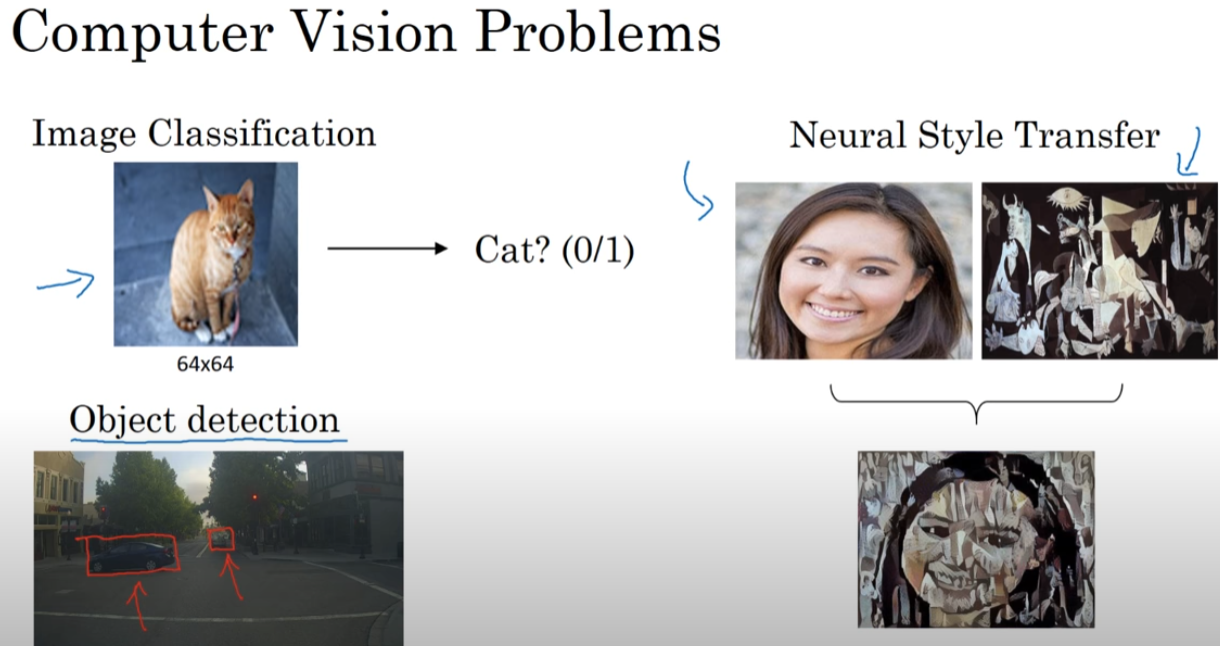
- Facial Recognition: Used in security systems and social media tagging.
- Medical Imaging: Helps in detecting diseases using X-rays, MRIs, and CT scans.
- Autonomous Vehicles: Enables self-driving cars to recognize objects and road signs.
- Industrial Automation: Used for defect detection in manufacturing.
Fundamental Concepts
- Pixels: The smallest unit in an image.
- Grayscale and Color Images: Difference between single-channel and multi-channel images.
- Resolution: Number of pixels in an image.
- Image Representation: Images as matrices of pixel values.
Mathematical Formulation
An image can be represented as a matrix:
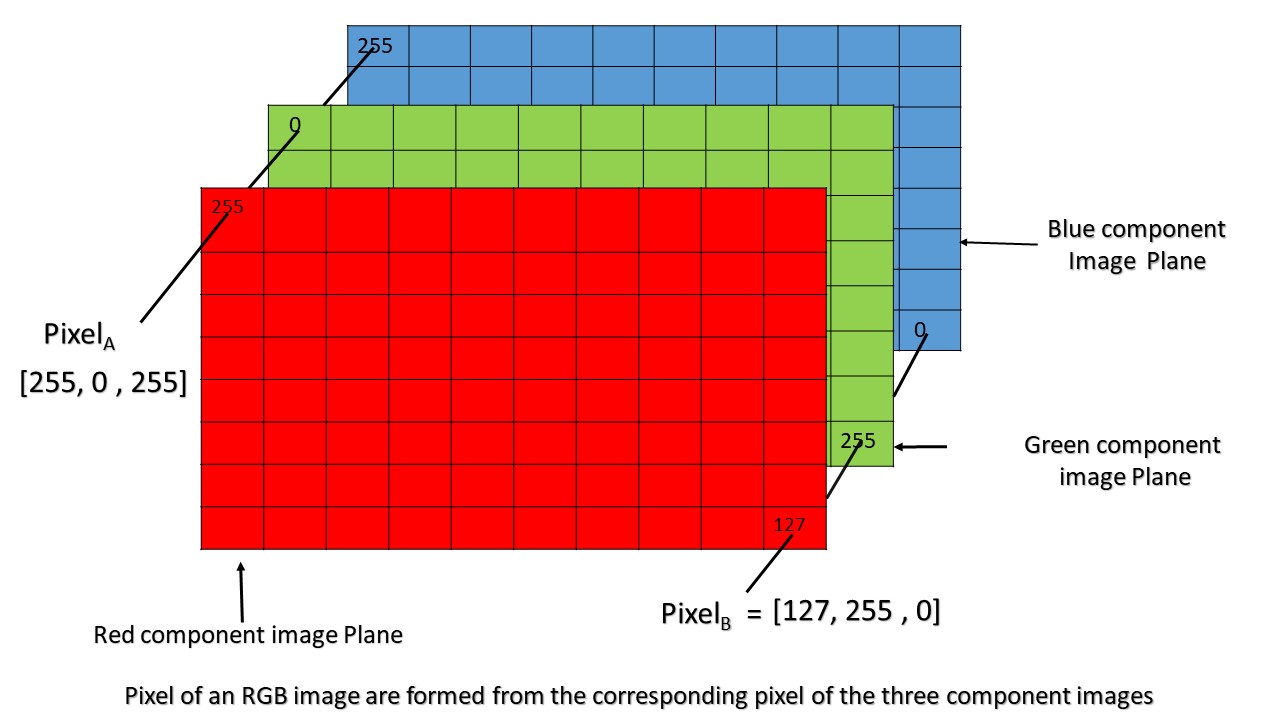
where and represent height and width, and represents the number of color channels (1 for grayscale, 3 for RGB images).
Edge Detection
Why Use Convolution for Edge Detection?
Edge detection aims to find points in an image where the intensity changes sharply. These points often correspond to boundaries of objects, texture changes, or discontinuities in depth. To detect these changes, we apply convolution operations with specific filters.
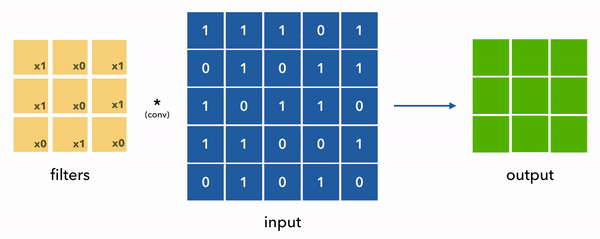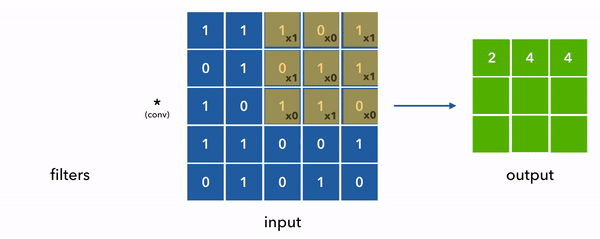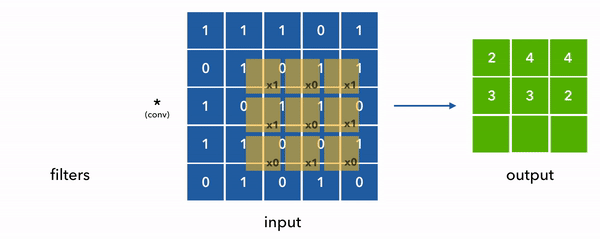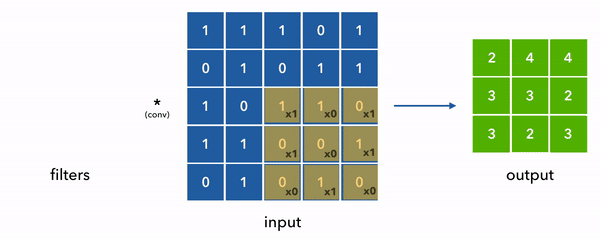
Convolution is a mathematical operation that helps us apply a small matrix (called a filter or kernel) across the entire image to detect specific patterns like edges.
What Does a Filter Do?
A filter is essentially a small grid of numbers (e.g., ) that slides across the image and emphasizes certain features:
- Edge filters highlight intensity changes
- Blur filters smooth the image
- Sharpening filters enhance details
In edge detection, filters are designed to detect high spatial frequency changes—essentially, edges.
Mathematical Example
We apply a vertical Sobel filter :
This filter detects vertical edges by highlighting horizontal intensity transitions.
Step-by-Step Convolution (No Padding, Stride = 1)
Let’s compute the top-left value of the output matrix. We place the filter on the top-left 3x3 window of ( I ):
Window:
Element-wise multiplication and sum:
So, the top-left value of the output matrix is 16.
Second Convolution Step (Next to Right)
New window (move filter one step to the right):
Apply the same operation:
So, second value is -13.
Full Output Matrix (4x4)
After sliding the filter across the 6x6 image, we get the 4x4 output:
This matrix highlights the vertical edges in the original image—areas where pixel intensities change most dramatically from left to right.
The result of convolving the image with these filters gives us areas of strong gradient—edges.
Key Insight:
Filters translate the idea of change in pixel values into a computable quantity.
Edge Detection Techniques
1. Sobel Operator
- Combines Gaussian smoothing and differentiation.
- Horizontal () and vertical () gradients are calculated using predefined 3x3 kernels.
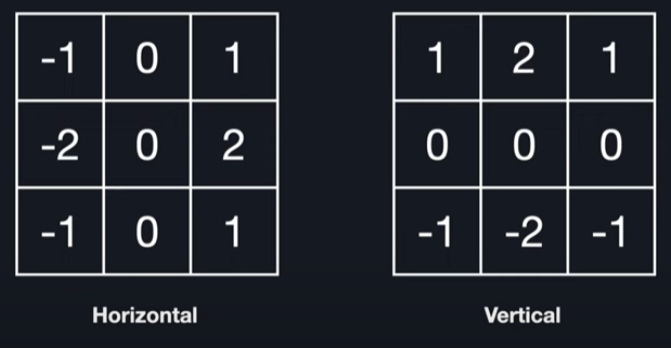
- The gradient magnitude is:
- Commonly used due to simplicity and noise resistance.
- Watch this youtube video
2. Prewitt Operator
- Similar to Sobel, but with uniform weights.
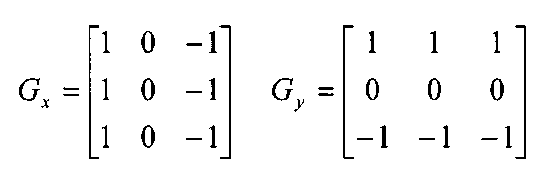
- Slightly less sensitive to noise compared to Sobel.
3. Laplacian of Gaussian (LoG)
- A second derivative method.
- Detects edges by identifying zero-crossings after applying the Laplacian to a Gaussian-smoothed image.
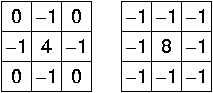
- Equation:
- Sensitive to noise, hence Gaussian smoothing is applied first.
4. Canny Edge Detection
A multi-stage algorithm designed for optimal edge detection:
- Gaussian Filtering: Noise reduction.
- Gradient Calculation: Using Sobel filters.
- Non-Maximum Suppression: Thinning the edges.
- Double Thresholding: Classify edges as strong, weak, or non-edges.
- Hysteresis: Connect weak edges to strong ones if they are adjacent.
Canny is widely used in practice for its high accuracy and low false detection.
5. Difference of Gaussians (DoG)
- Approximates the LoG by subtracting two Gaussian-blurred images:
- Faster to compute than LoG.
- Used in blob detection and feature matching.
Convolutional Operations
Padding
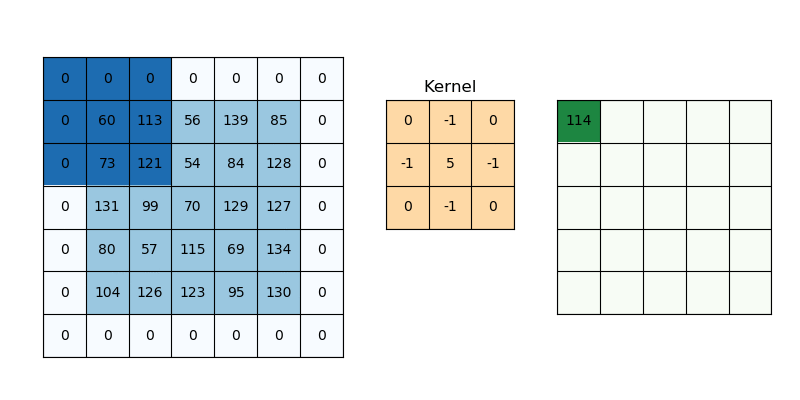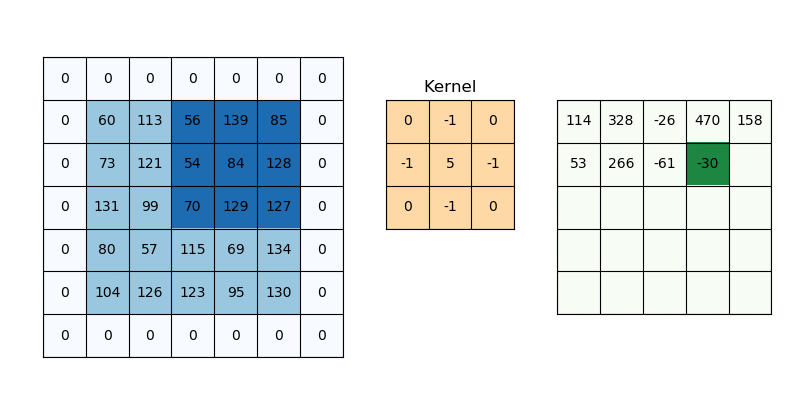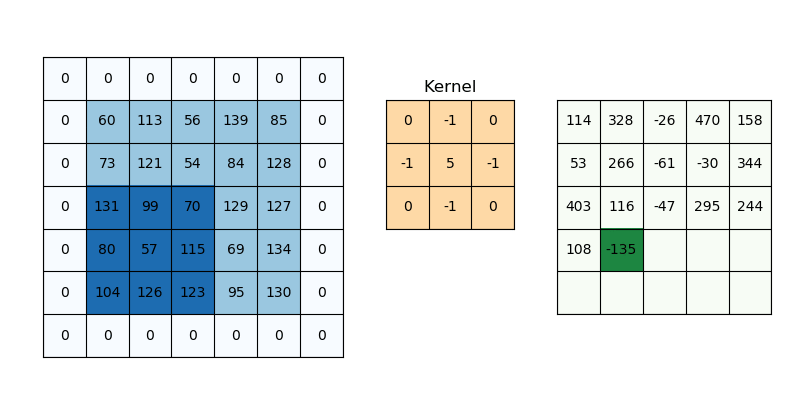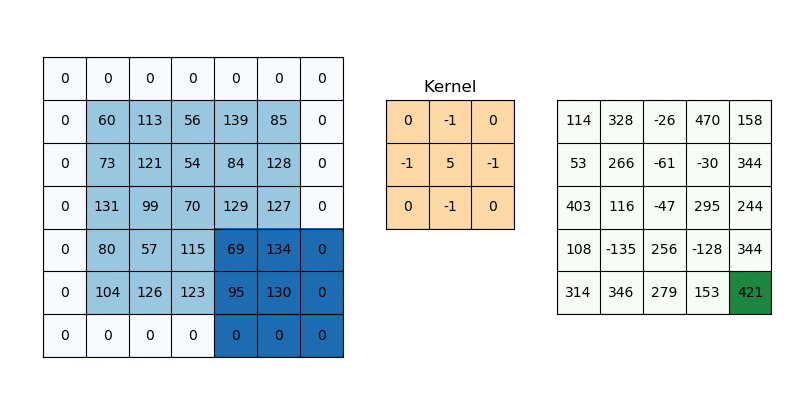
Why Padding is Needed
When applying convolution, the output image shrinks unless we pad it. This is a problem when building deep networks where spatial dimensions shrink after each convolution.
Without Padding:
Where:
- : input size
- : filter size
Example
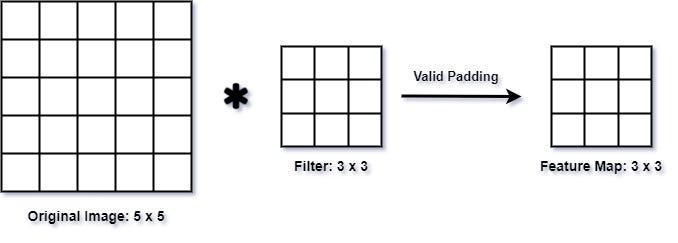
In this image:
- : input size =
- : filter size =
With Padding ():
Where:
- : input size
- : filter size
- : padding size
Example
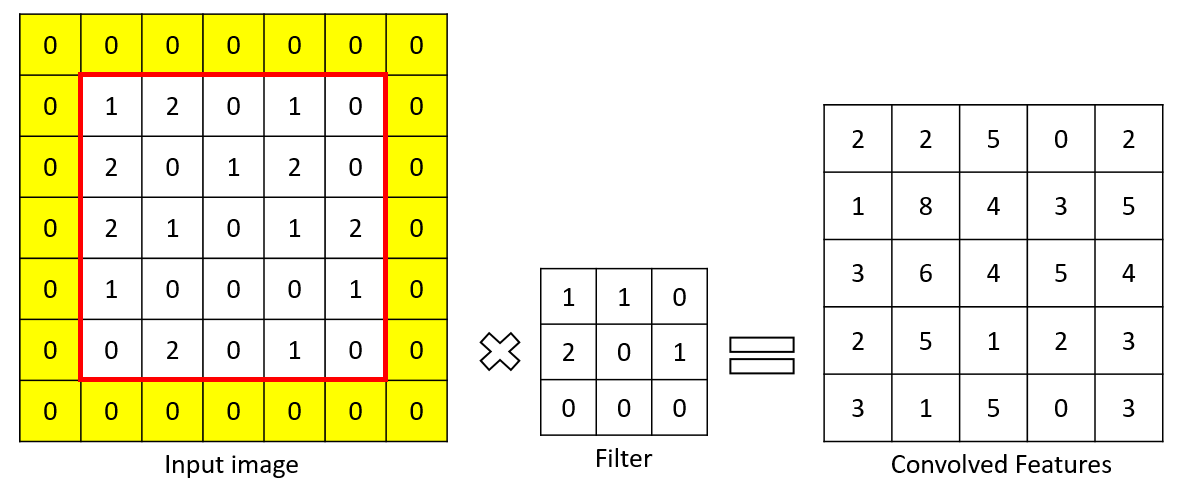
In this image:
- : input size =
- : filter size =
- : padding size =
Types of Padding
- Valid Padding (no padding): Output is smaller.
- Same Padding (zero padding): Output size equals input size.
Real-World Analogy
Imagine scanning a photo with a magnifying glass: without padding, you can’t examine the borders. Padding extends the image so that every pixel gets equal attention.
Strided Convolutions
What is Stride?
Stride is the number of pixels the filter moves at each step.
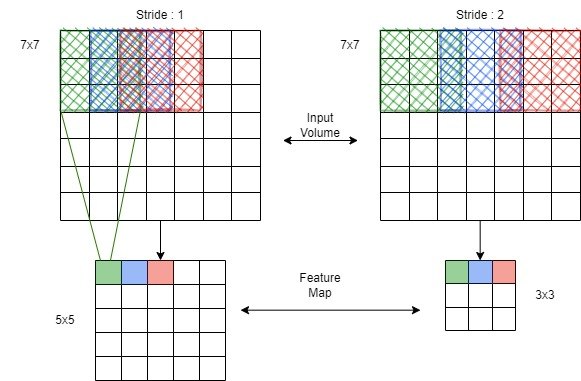
- Stride = 1: Normal convolution (moves 1 pixel at a time)
- Stride = 2: Downsampling (moves 2 pixels at a time)
Output Size Formula
Where:
- : input size
- : filter size
- : stride
- : padding
Visual Example
If stride = 2, the filter skips every alternate pixel, effectively reducing the spatial size of the output.
Convolutions Over Volume
From 2D to 3D
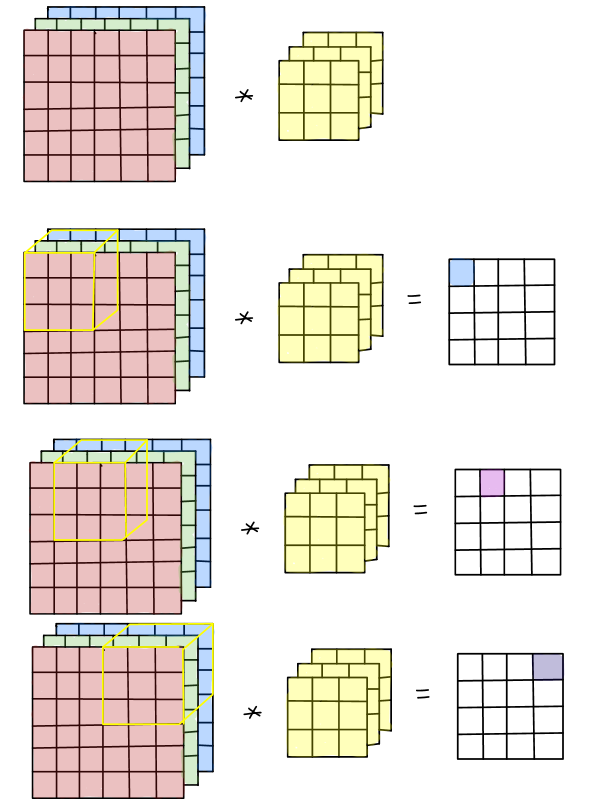
In RGB images, we have 3 channels: Red, Green, and Blue. Thus, a convolutional layer operates over 3D volumes.
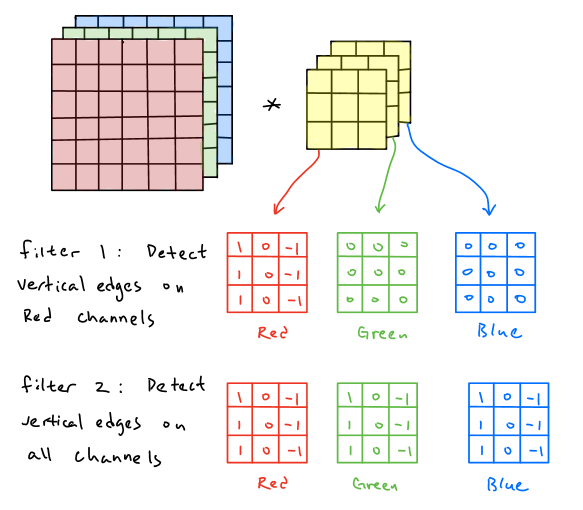
Input Dimensions:
- : Height
- : Width
- : Channels (e.g., 3 for RGB)
Filter Dimensions:
- Number of filters:
Output Volume:
- Each filter creates a 2D activation map, stacked together to form the output volume.
Practical Example
Let’s say you have a (6, 6, 3) image, and you apply 2 filters of size (3, 3, 3):
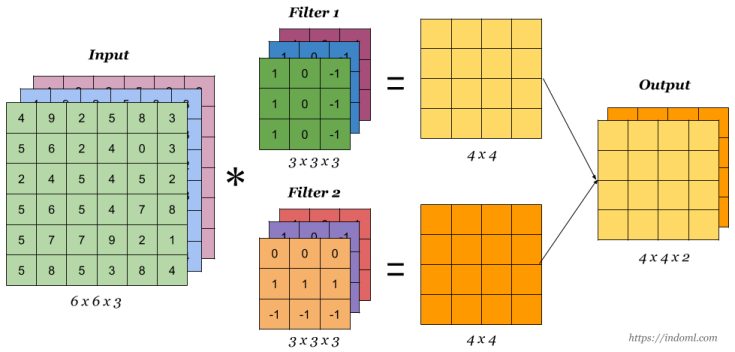
- Output shape: (4, 4, 2) (assuming valid padding, stride=1)
CNN Architecture and Examples
1. One Layer of a Convolutional Network
A Convolutional Neural Network (CNN) is typically composed of three types of layers:
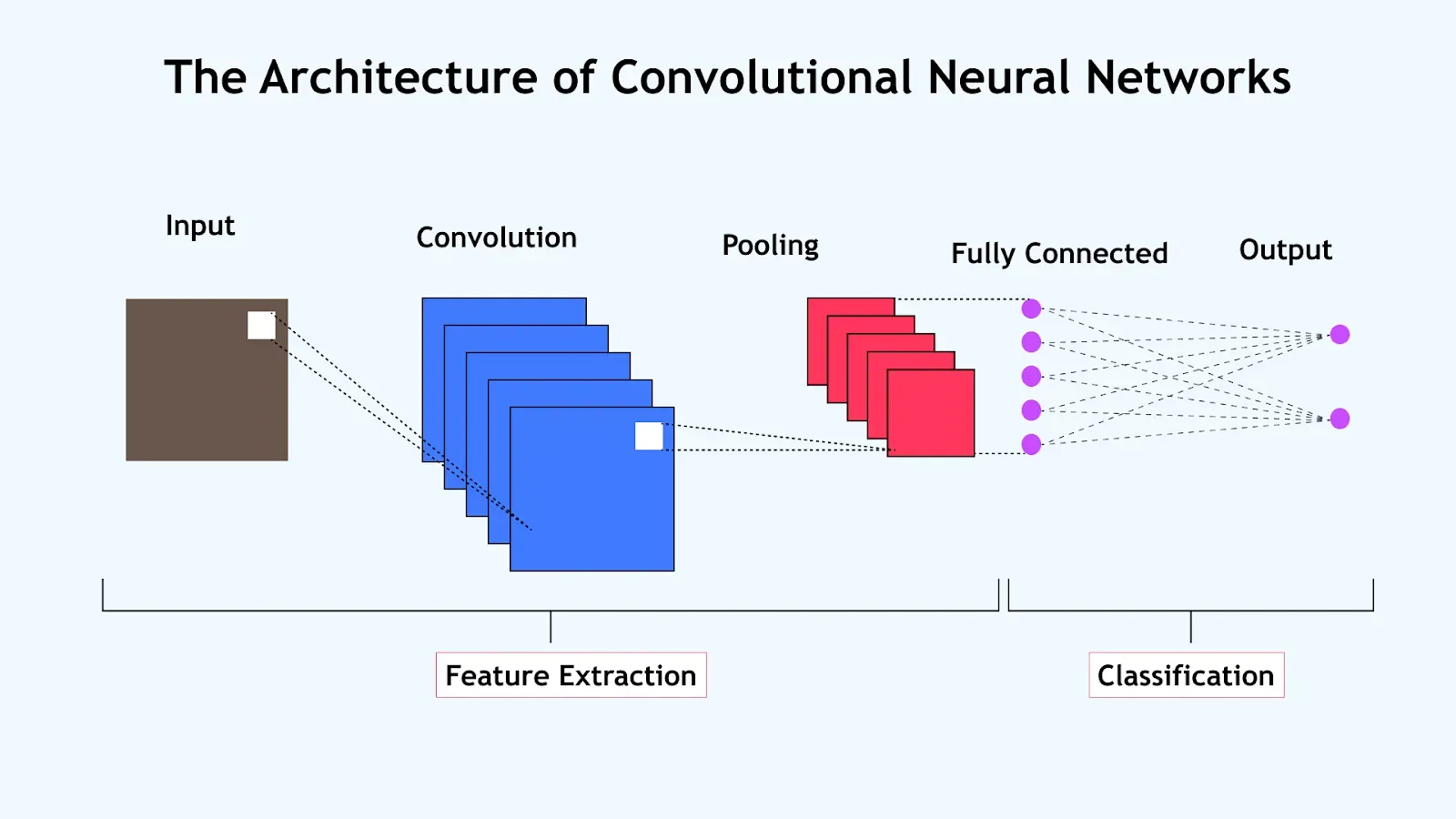
- Convolutional layers: Apply filters to extract spatial features.
- Pooling layers: Downsample feature maps to reduce computation.
- Fully connected layers: Perform final classification or regression.
Each layer transforms the input volume into an output volume through learnable parameters or fixed operations.
Layer Types of CNN
1. Convolutional Layers
Purpose:
To extract spatial features such as edges, textures, and patterns by sliding filters over the input image or feature map.
How it works:
- A filter (or kernel) of size slides over the input.
- At each location, an element-wise multiplication is performed between the filter and the part of the input it overlaps.
- The results are summed to produce a single number in the output feature map.
Mathematical Operation:
Let the input be and the filter be .
Example:
Input: grayscale image with filter:
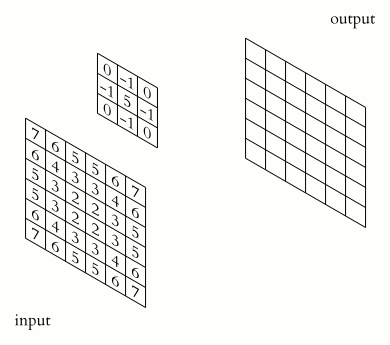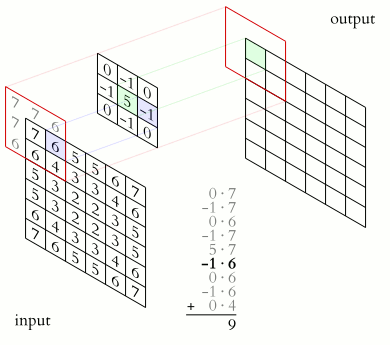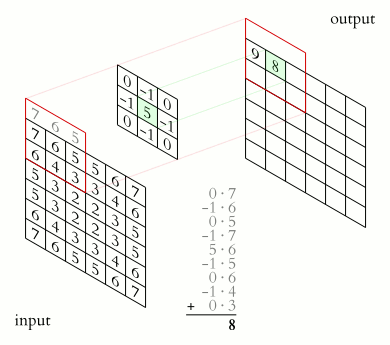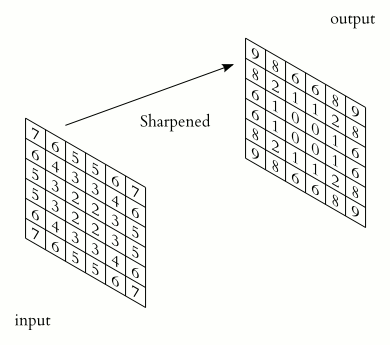
As the filter slides across the input, it detects vertical and horizontal edges by producing high activation in regions with strong center transitions.
2. Pooling Layers
Purpose:
To reduce the spatial dimensions (height and width) of the feature maps, thereby:
- Reducing the number of parameters and computation
- Controlling overfitting
- Making the model invariant to small translations in the input
Types:
Max Pooling:
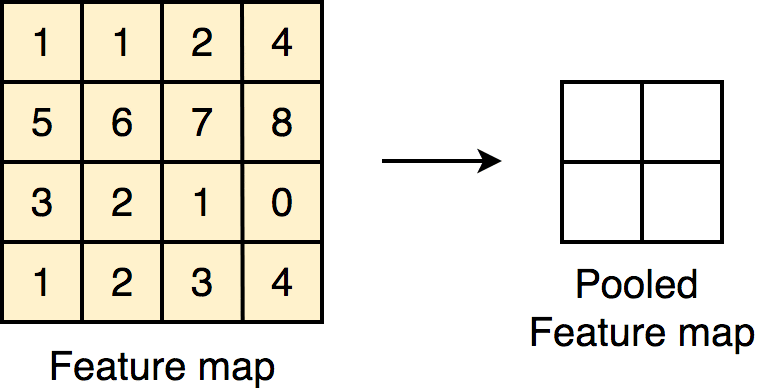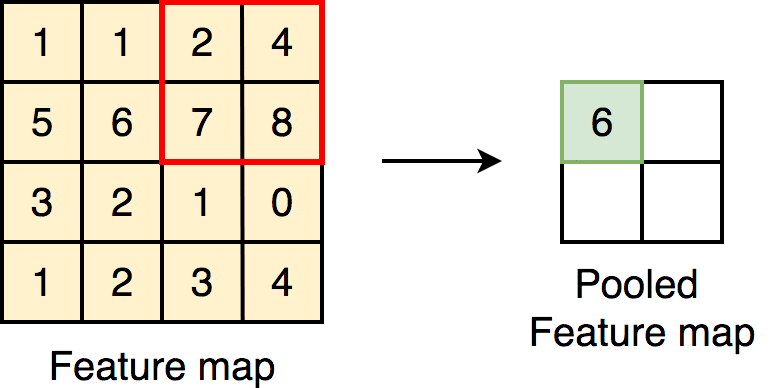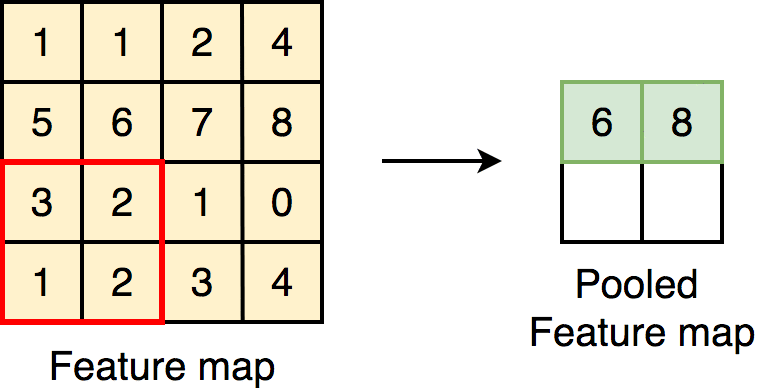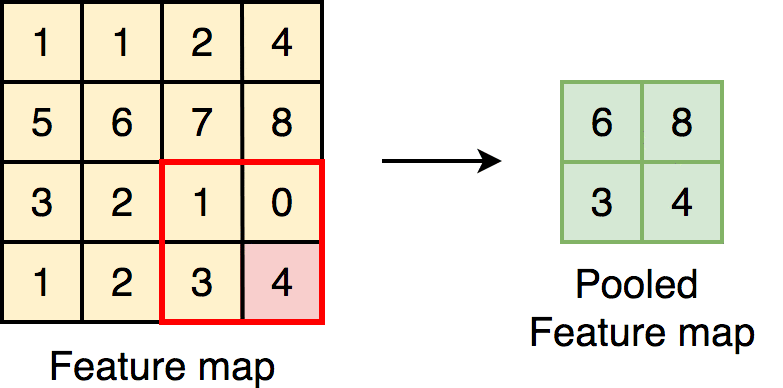
Selects the maximum value in each region.
Average Pooling:
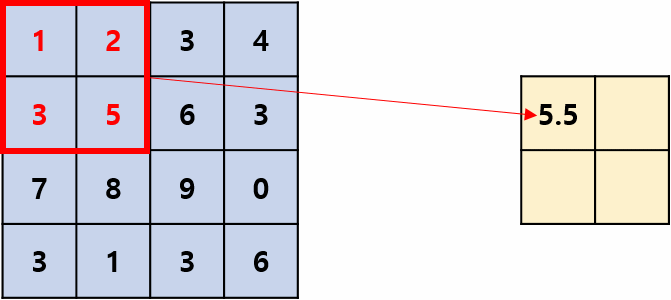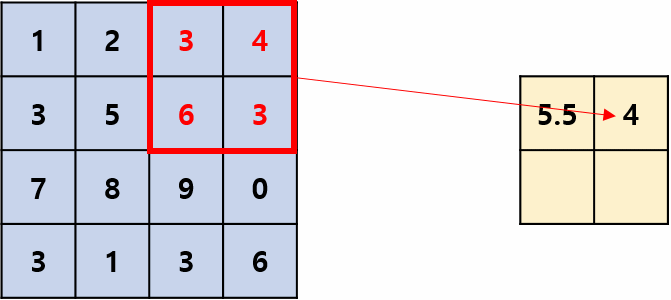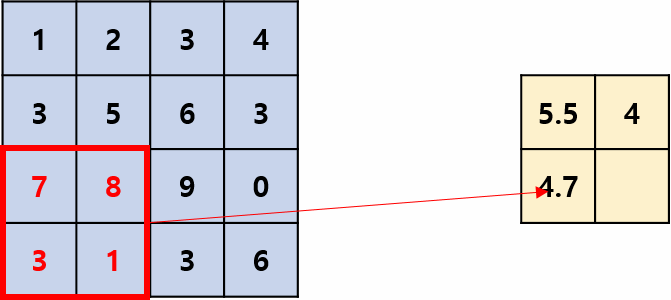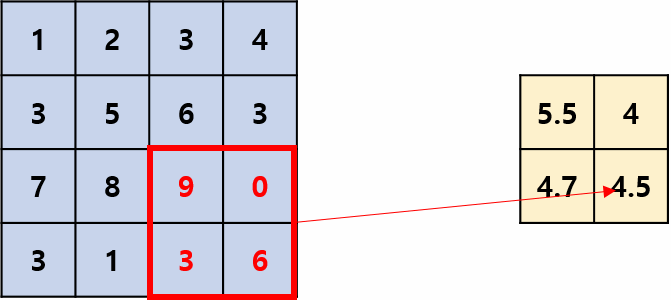
Takes the average of values in each region.
3. Fully Connected Layers
To connect every neuron in one layer to every neuron in the next layer, performing the final classification or regression.
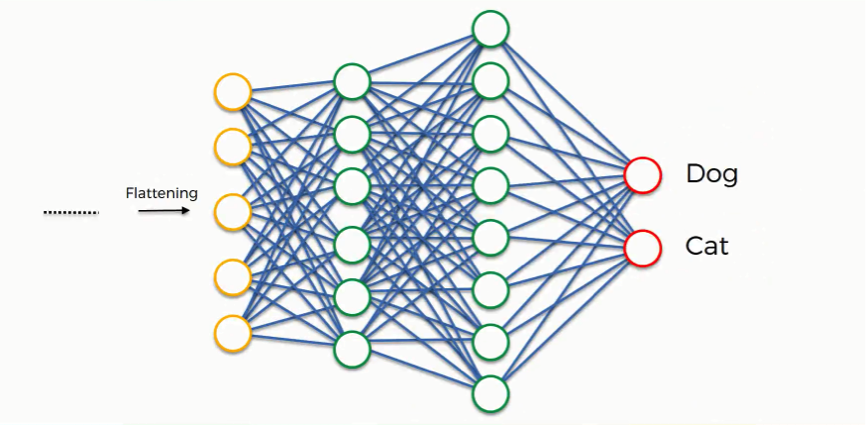
How it works:
- Takes the flattened output from the last convolutional/pooling layer
- Passes it through one or more dense layers
- Final layer often uses softmax for classification
Mathematical Form:
Given the input vector , weights , and bias :
Example:
Let’s say we have a feature map output size of from the last pooling layer:
- FC1: 400 → 120 (ReLU)
- FC2: 120 → 84 (ReLU)
- FC3: 84 → 10 (Softmax, for 10-class classification)
These dense layers combine all the high-level features learned in the earlier layers and output a prediction.
Summary Table
| Layer Type | Role | Typical Parameters | Output Shape Transformation |
|---|---|---|---|
| Convolutional | Extract local spatial features | , , , filters | |
| Pooling | Downsample feature maps | , | |
| Fully Connected | Final classification/regression | neurons per layer | (vector size) |
These layers together form the foundation of Convolutional Neural Networks, enabling them to learn hierarchical representations from raw pixels to abstract concepts.
Notation and Terminology
- : height and width of the input volume
- : number of channels (depth)
- : filter size
- : stride
- : padding
- , : weights and biases at layer
Parameters and Learnable Components
- Weights (): Represent filters; shared spatially across the input.
- Biases (): One per filter.
- Activation (): Output of ReLU or other non-linear function.
Each neuron in a layer is connected only to a small region of the previous layer, leading to sparse interactions and parameter sharing.
3. CNN Example (Comprehensive Network)
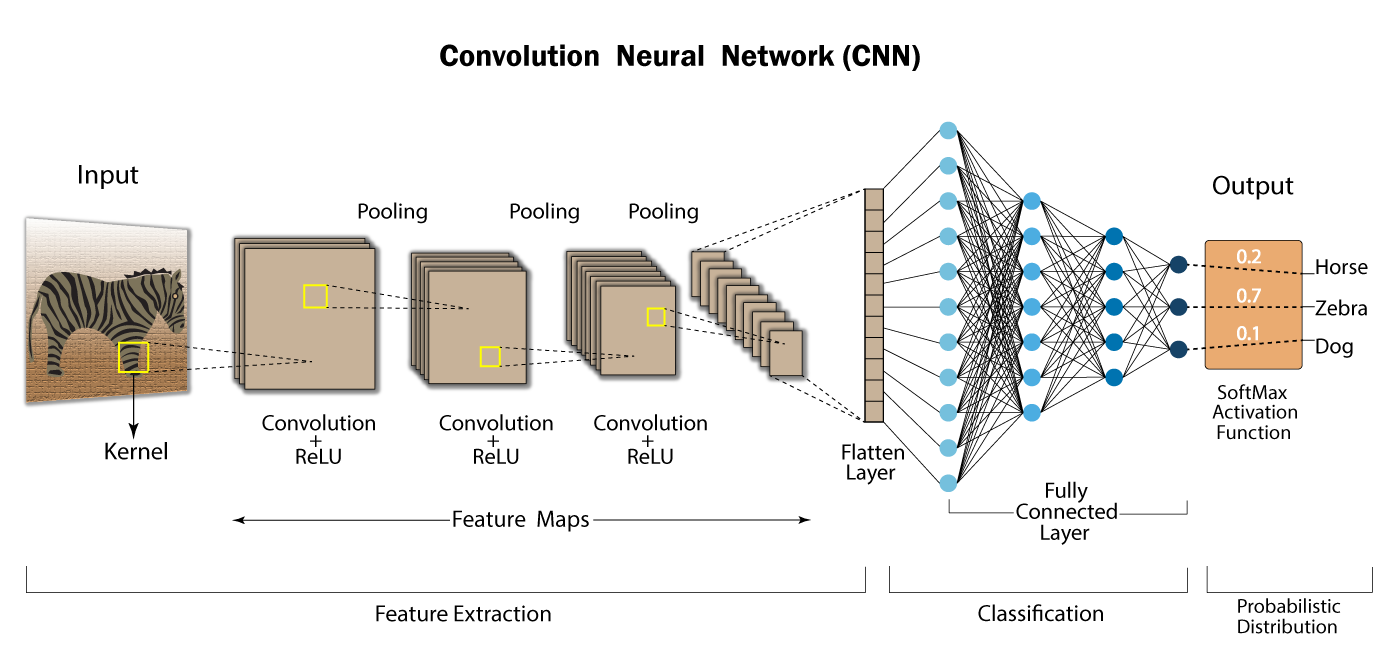
Why Convolutions?
Convolutional layers are the cornerstone of modern deep learning models in computer vision, replacing traditional fully connected layers in image tasks. This section explores why convolutions are used instead of dense layers, and what advantages they bring.
1. The Limitations of Fully Connected Layers for Images
a. Parameter Explosion
A fully connected (dense) layer connecting every pixel of an image to every neuron in the next layer requires a huge number of parameters.
Example:
- Input image size:
- Fully connected layer with 1000 neurons:
This leads to high memory usage, overfitting risk, and long training times.
b. Ignores Spatial Structure
Dense layers treat input features independently and do not take advantage of the spatial locality of image data.
- A cat’s ear in the top-left and bottom-right corners are treated as unrelated by dense layers.
2. Benefits of Convolutional Layers
a. Sparse Interactions
Each output neuron is connected only to a small region of the input (called the receptive field).
- Fewer parameters
- Faster computations
Example:
- Using instead of connecting all 12,288 pixels
b. Parameter Sharing
Same filter (weights) is applied across the entire image:
This results in drastic reduction in number of parameters and allows feature detection to be translation invariant.
c. Translation Equivariance
- If an object moves in the image, its feature map also moves.
- The model learns position-independent features — important for generalization.
Classic Networks: LeNet-5, AlexNet, VGG
- Why Look at Classic Networks?
- LeNet-5 (1998, Yann LeCun)
- AlexNet (2012, Alex Krizhevsky, Ilya Sutskever, Geoffrey Hinton)
- VGG Networks (2014, Visual Geometry Group, Oxford)
- Summary Table
- Final Thoughts
In the early stages of deep learning and computer vision, several foundational convolutional neural network (CNN) architectures shaped the field and enabled significant breakthroughs in image recognition. In this document, we explore three of the most historically significant and technically influential networks: LeNet-5, AlexNet, and VGG.
These architectures demonstrate the progression of CNN design from shallow, simple models to deeper, more powerful systems capable of scaling to large datasets like ImageNet.
Why Look at Classic Networks?
Understanding classic CNN architectures is essential for the following reasons:
- They introduce fundamental building blocks (e.g., convolutional layers, pooling layers, ReLU activation).
- They highlight challenges faced at different stages of deep learning evolution (e.g., overfitting, vanishing gradients).
- They provide insights into the design philosophy of modern deep architectures.
LeNet-5 (1998, Yann LeCun)
Overview
LeNet-5 was one of the earliest CNN models designed to recognize handwritten digits (e.g., MNIST dataset). It demonstrated the power of learned convolutional filters combined with a small number of parameters.
Architecture
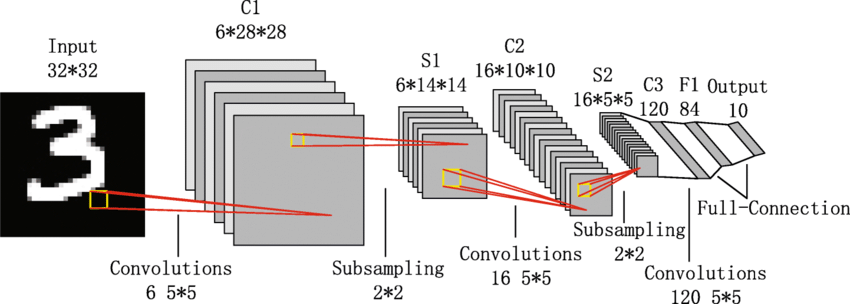
- Input: 32x32 grayscale image
- C1: Convolutional layer with 6 filters of size 5x5 → output: 28x28x6
- S2: Subsampling (average pooling) layer → output: 14x14x6
- C3: Convolutional layer with 16 filters → output: 10x10x16
- S4: Subsampling layer → output: 5x5x16
- C5: Fully connected convolutional layer → output: 120
- F6: Fully connected layer → output: 84
- Output: 10-class softmax layer
Parameters
LeNet uses shared weights, reducing the number of parameters compared to fully connected networks.
Insights
- Introduced the idea of local receptive fields, weight sharing, and subsampling.
- Excellent for small datasets but struggles with large-scale data due to its shallow depth.
AlexNet (2012, Alex Krizhevsky, Ilya Sutskever, Geoffrey Hinton)
Breakthrough
AlexNet marked the first major success of deep learning in the ImageNet Large Scale Visual Recognition Challenge (ILSVRC 2012), achieving top-5 error of 15.3%, compared to 26% for the runner-up.
Architecture
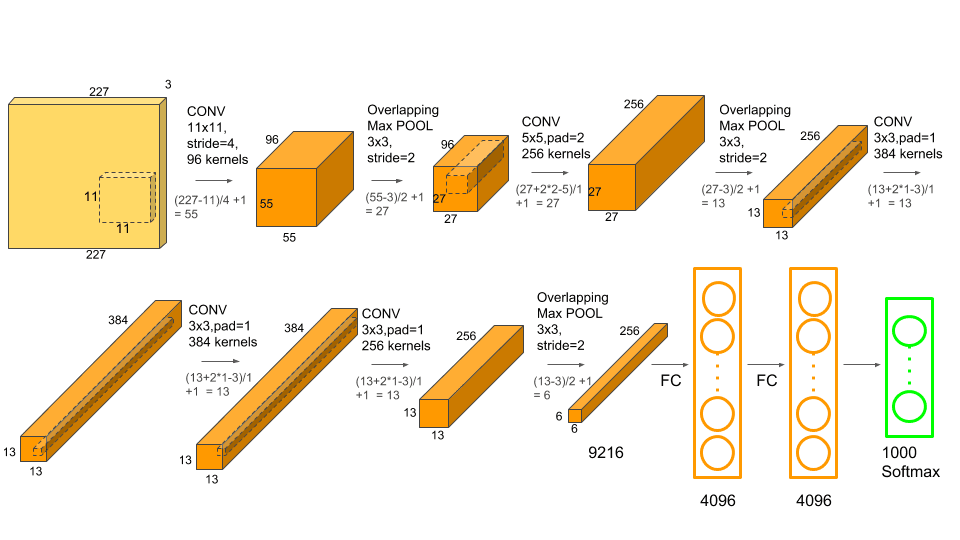
- Input: 224x224x3 RGB image
- Conv1: 96 filters of 11x11, stride 4 → 55x55x96
- MaxPool1: 3x3, stride 2 → 27x27x96
- Conv2: 256 filters of 5x5 → 27x27x256
- MaxPool2: 3x3 → 13x13x256
- Conv3: 384 filters of 3x3 → 13x13x384
- Conv4: 384 filters of 3x3 → 13x13x384
- Conv5: 256 filters of 3x3 → 13x13x256
- MaxPool3: 3x3 → 6x6x256
- FC6: Fully connected layer with 4096 neurons
- FC7: Fully connected layer with 4096 neurons
- FC8: 1000-way softmax layer
Key Innovations
- Used ReLU (Rectified Linear Unit) instead of sigmoid or tanh → faster training
- Introduced dropout for regularization
- Trained on two GPUs in parallel
Insights
- Showed the world that deep networks could outperform traditional machine learning models if trained with large datasets and GPUs.
VGG Networks (2014, Visual Geometry Group, Oxford)
VGG emphasized simplicity and depth: using small 3x3 filters and stacking them deeply to capture complex patterns.
Architecture (VGG-16)
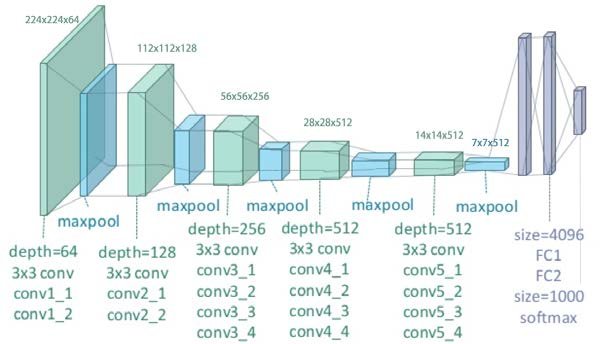
- Input: 224x224x3 RGB image
- Stack of 13 convolutional layers using 3x3 filters
- 5 max-pooling layers to reduce spatial dimensions
- 3 fully connected layers, with the last one as a softmax for classification
Example:
- Conv3-64 → Conv3-64 → MaxPool
- Conv3-128 → Conv3-128 → MaxPool
- Conv3-256 → Conv3-256 → Conv3-256 → MaxPool
- Conv3-512 → Conv3-512 → Conv3-512 → MaxPool
- Conv3-512 → Conv3-512 → Conv3-512 → MaxPool
- FC-4096 → FC-4096 → Softmax(1000)
Characteristics
- Consistent use of 3x3 filters simplifies the design and enables deeper networks
- Requires significant memory and computation (hundreds of millions of parameters)
Insights
- Demonstrated that depth is a key factor in improving CNN performance
- The architecture became a benchmark and inspired many follow-up models
Summary Table
| Model | Year | Input Size | Depth | Unique Aspects |
|---|---|---|---|---|
| LeNet-5 | 1998 | 32x32 | 7 | Local receptive fields, subsampling |
| AlexNet | 2012 | 224x224x3 | 8 | ReLU, dropout, GPU parallelism |
| VGG-16 | 2014 | 224x224x3 | 16 | Simplicity, 3x3 filters, depth |
Final Thoughts
These classic CNN architectures form the backbone of modern computer vision systems. Each contributed key architectural innovations that addressed specific challenges in training deep networks.
Understanding them allows us to appreciate the evolution of deep learning and to better design models suited for today's massive data and compute resources.
Modern CNN Architectures: ResNet, Inception, MobileNet, EfficientNet
ResNet: Deep Residual Networks
As neural networks became deeper, researchers observed a counterintuitive phenomenon: deeper networks often performed worse during training and testing compared to shallower ones. This degradation was not due to overfitting but rather an optimization issue.
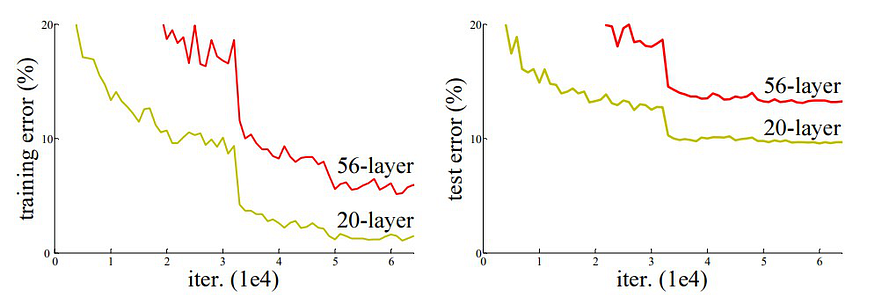
This problem is called the degradation problem. It shows that simply stacking more layers doesn't guarantee better accuracy — instead, it often leads to higher training error. This contradicts our expectations, since deeper models should be able to represent more complex functions.
To address this, ResNet introduced the concept of residual learning.
Residual Learning: Core Idea
Instead of learning a direct mapping , ResNet proposes to learn the residual function:
This reformulation allows the network to focus on learning the difference between the input and output, which is often easier to optimize.
The output of a residual block is:
where is the output from a few stacked layers (e.g., 2 Conv-BN-ReLU layers) and is the original input. This addition is known as a skip connection or shortcut connection.
Here's the basic structure of a Residual Block:
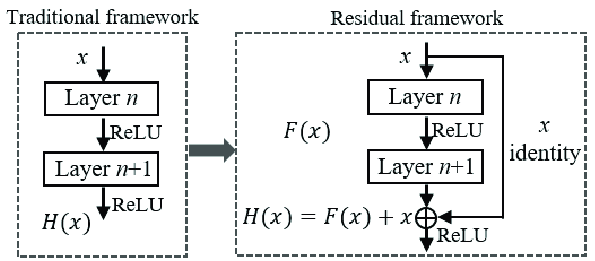
- If the input and output dimensions differ, a 1x1 convolution is used to match dimensions before addition.
- This structure allows gradients to flow more easily during backpropagation, mitigating the vanishing gradient problem.
Identity Shortcut Connection
This is the key innovation. By allowing the input to bypass intermediate layers, the model can preserve useful features, learn identity mappings when needed, and avoid overfitting.
Shortcut types:
- Identity shortcut: When input and output dimensions match
- Projection shortcut: 1x1 convolution used to match shapes
Why ResNets Work?
- Improved Gradient Flow: Easier to train deep networks due to unblocked gradient paths
- Easier Optimization: Residual mapping simplifies the learning process
- Deeper Networks: Can train very deep networks (e.g., ResNet-152) without degradation
- Better Generalization: Performs well across image classification, detection, segmentation
Forward and Backward Propagation
In a residual block, during forward propagation, the shortcut allows direct data flow from earlier layers. In backward propagation, the gradient can pass through both the residual path and shortcut connection, reducing gradient vanishing.
Let’s say the loss gradient is . Then:
Here, is the identity matrix, ensuring that gradient doesn’t vanish even if becomes small.
Real-World Analogy
Imagine you’re assembling a piece of furniture using instructions. Instead of reading and understanding every step from scratch (direct mapping), you compare each step with what you’ve already done (residual comparison). It’s easier to notice what's missing and fix it.
Variants of ResNet
- ResNet-18, 34, 50, 101, 152: Increasing depth
- ResNeXt: Groups of convolutions
- Pre-activation ResNet: Moves BN and ReLU before convolutions
Inception and 1x1 Convolutions
Networks in Networks and 1x1 Convolutions
In 2014, the "Network in Network" architecture introduced the idea of using 1x1 convolutions — a surprisingly powerful and efficient technique in modern CNNs.
What is a 1x1 Convolution?
- A 1x1 convolution applies a filter of size across all input channels.
- Though the spatial dimension () seems trivial, it processes channel-wise information and mixes features across depth.
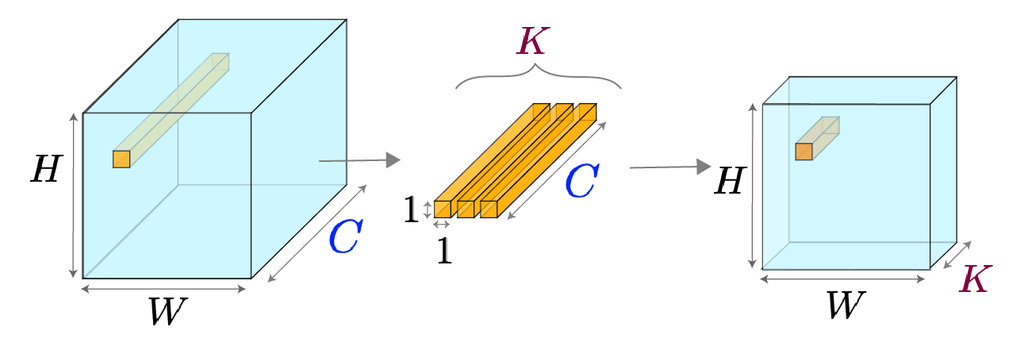
Let’s assume an input of shape . Applying 1x1 filters produces an output of shape .
Why is it useful?
- Dimensionality Reduction: You can reduce the number of channels before applying computationally expensive filters (e.g., 3x3, 5x5), reducing the model size and speed requirements.
- Increase Non-Linearity: When combined with non-linear activations (like ReLU), it increases the representational power of the network.
- Lightweight Computation: Compared to a standard 3x3 convolution with the same input/output dimensions, the FLOPs (floating point operations) required are significantly lower.
Intuition:
Think of 1x1 convolution as a way to relearn combinations of channels at each spatial location. It’s like assigning weights to each feature and mixing them in a smart way — like forming new meanings from known "ingredients."
Inception Network
CNNs originally used sequential layers — stacking 3x3 or 5x5 filters one after another. But why settle for a single filter size?
Some patterns might be better captured with:
- 1x1 (fine details)
- 3x3 (mid-level features)
- 5x5 (larger context)
Key Insight:
Why not apply all of them in parallel, and let the network decide which one is best?
That’s the core idea behind the Inception Module.
Problem:
Applying multiple large filters in parallel increases computation exponentially.
GoogLeNet and Inception Blocks
The GoogLeNet (Inception-v1) architecture introduced the Inception module to allow multi-scale feature extraction while keeping the computation affordable.
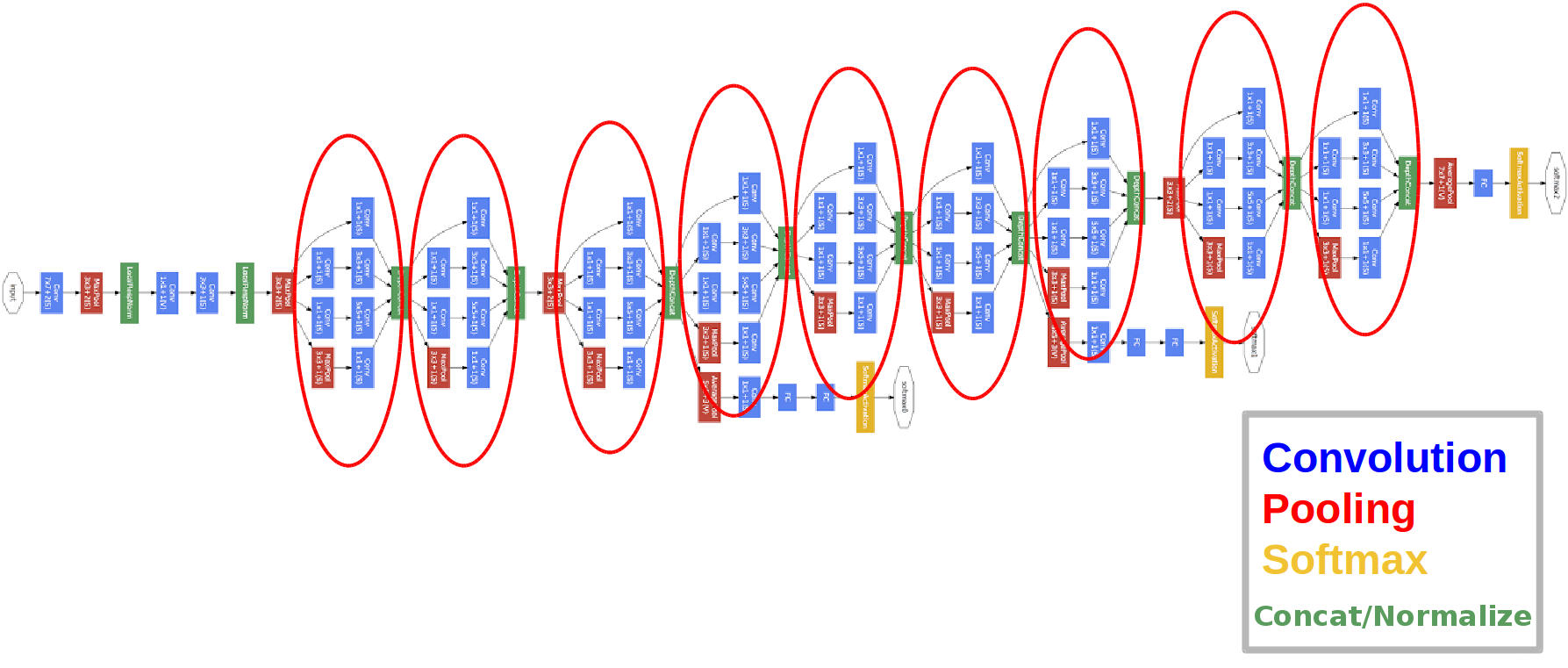
Structure of an Inception Block:
Each Inception block has multiple branches:
- 1x1 convolution
- 1x1 → 3x3 convolution
- 1x1 → 5x5 convolution
- 3x3 max pooling → 1x1 convolution
Notice how each expensive convolution is preceded by a 1x1 convolution for dimensionality reduction.
Advantages:
- Parameter Efficiency: Fewer parameters than naïvely stacking all filters.
- Rich Feature Learning: Learns features at multiple receptive fields simultaneously.
- Parallelism: More effective than deeper or wider models with uniform layers.
Example:
Assume an input of size . After passing through an Inception module, we may get something like:
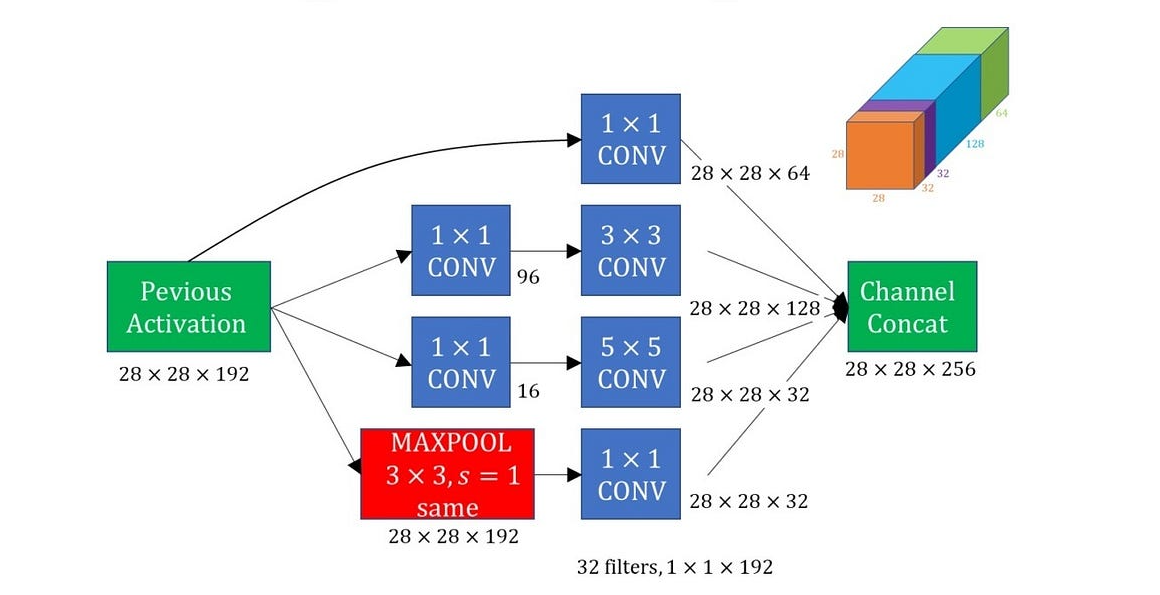
- 1x1 branch → 64 channels
- 3x3 branch → 128 channels
- 5x5 branch → 32 channels
- Pooling branch → 32 channels
- Total output depth: 256
Improvements Over Time
GoogLeNet inspired many improved versions:
- Inception v2/v3: Factorization of convolutions (e.g., 5x5 → two 3x3 layers)
- Inception v4: Combined ideas from ResNet and Inception (e.g., Inception-ResNet)
- Use of BatchNorm and Auxiliary Classifiers
These tricks improved accuracy without dramatically increasing parameters.
The Inception architecture was a major leap forward in CNN design:
- It introduced the concept of multi-path architectures
- Emphasized computational efficiency
- Leveraged 1x1 convolutions to control model complexity
This paved the way for even more efficient models like MobileNet and EfficientNet.
MobileNet and EfficientNet
MobileNet
As deep learning models became larger and deeper, they demanded more memory and computation — not ideal for mobile or embedded devices. MobileNet, introduced by Google in 2017, addressed this challenge by proposing a highly efficient architecture using depthwise separable convolutions.
Standard Convolution vs. Depthwise Separable Convolution
Let’s recall the standard convolution:
Given an input of size , applying filters of size produces an output of size .
- Computation Cost:
MobileNet factorizes this into two steps:
-
Depthwise Convolution:
Apply one filter per input channel — no cross-channel combination.
Cost: -
Pointwise Convolution (1x1):
Mix the depthwise output with 1x1 filters.
Cost:
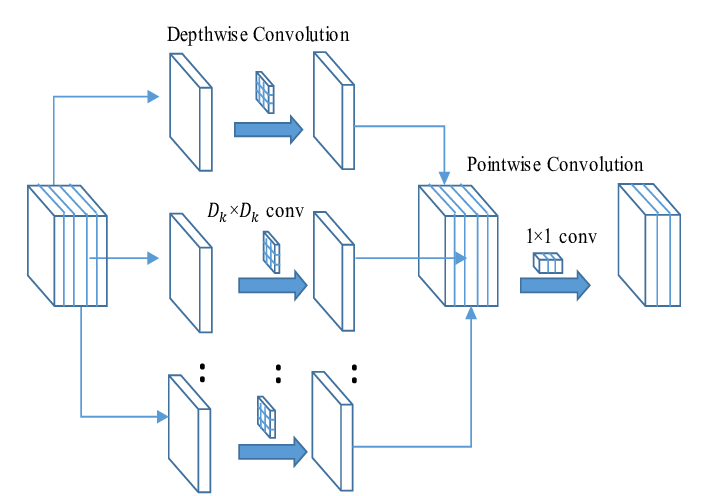
✅ Total Cost:
which is ~9x less than standard convolution when .
MobileNet Architecture (V1 Highlights)
MobileNetV1 is built by stacking depthwise separable convolutions instead of regular ones. It also introduces:
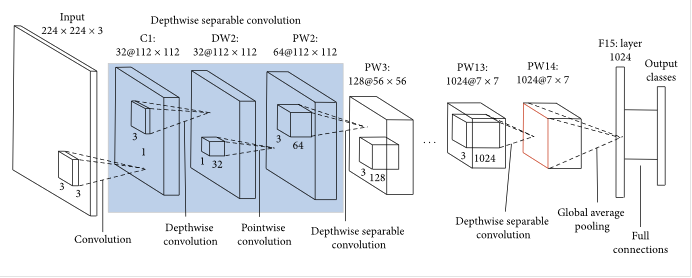
- Width Multiplier (α): Shrinks the number of channels (e.g., α=0.75 reduces model size).
- Resolution Multiplier (ρ): Reduces input image size to further save computation.
Together, these enable a trade-off between accuracy and resource usage.
MobileNet is often used as a backbone in real-time applications (e.g., object detection on smartphones, AR apps).
EfficientNet
Introduced in 2019 by Google AI, EfficientNet pushes the boundary of model performance by scaling neural networks systematically.
The Problem: How to Scale a CNN?
You can make a CNN more powerful by:
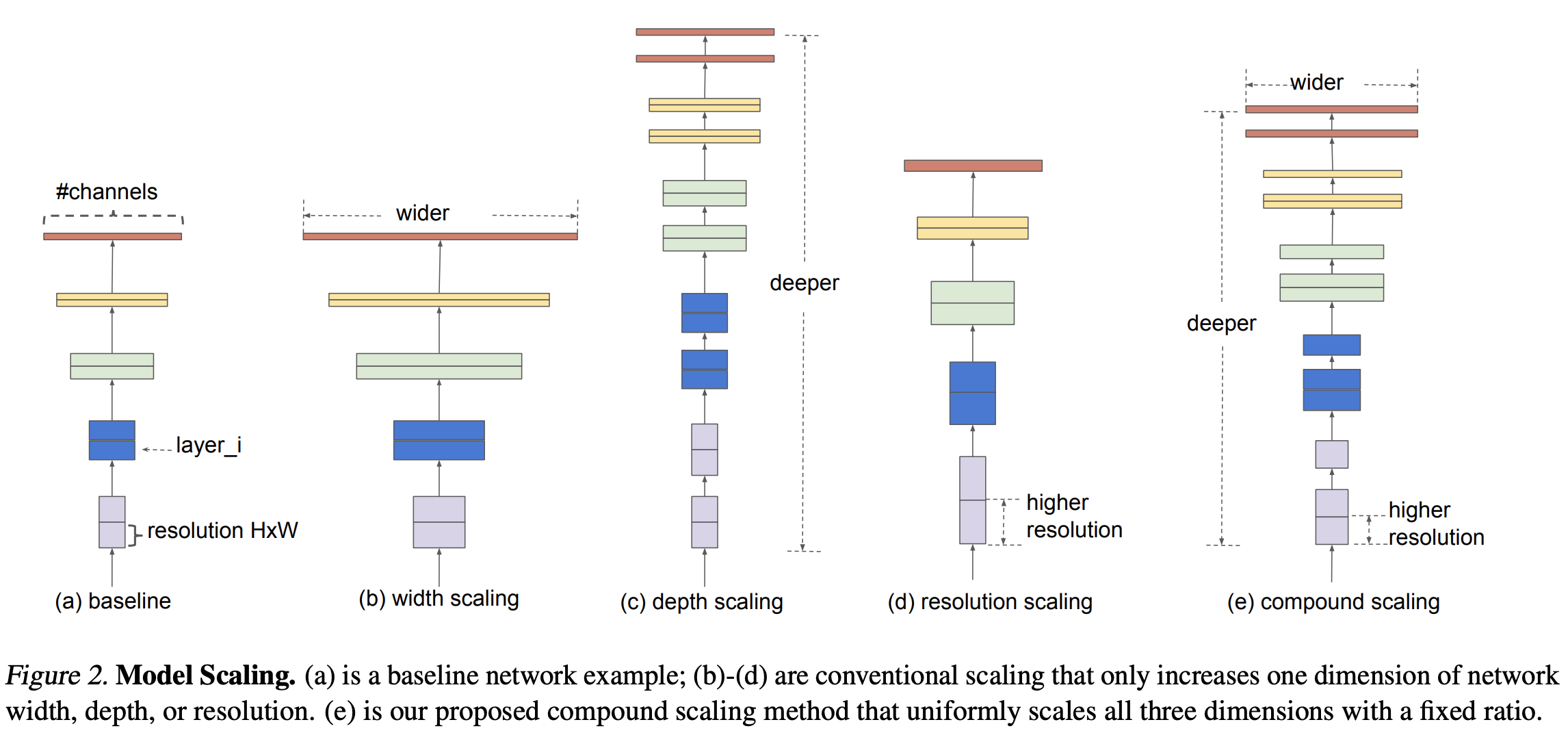
- Increasing depth (more layers)
- Increasing width (more channels)
- Increasing resolution (larger input images)
But how much of each?
Compound Scaling: Efficient Strategy
Instead of arbitrarily scaling one dimension, EfficientNet introduces a compound coefficient (ϕ) that balances all three:
- ϕ controls the available resources (e.g., more computation).
- α, β, γ are constants determined via grid search.
Performance
EfficientNet models (B0 to B7) are built on the same base architecture (EfficientNet-B0), with progressively larger values of ϕ.
- EfficientNet-B0: baseline
- EfficientNet-B1 to B7: scaled versions with increasing capacity
✅ Result:
EfficientNet achieves better accuracy with fewer parameters compared to deeper networks like ResNet-152 or Inception-v4.
| Architecture | Key Idea | Efficiency Trick |
|---|---|---|
| MobileNet | Lightweight model for mobile | Depthwise separable convolutions |
| EfficientNet | Scalable and accurate model | Compound scaling across depth, width, resolution |
Both architectures represent the evolution of CNN design towards compact, fast, and powerful models — a necessary shift for real-world AI deployment.
Object Localization and Detection
- Object Localization
- Landmark Detection
- Object Detection
- Sliding Window Approach and Its Convolutional Implementation
Object Localization
Object localization is the task of identifying the presence of an object in an image and determining its position using a bounding box.
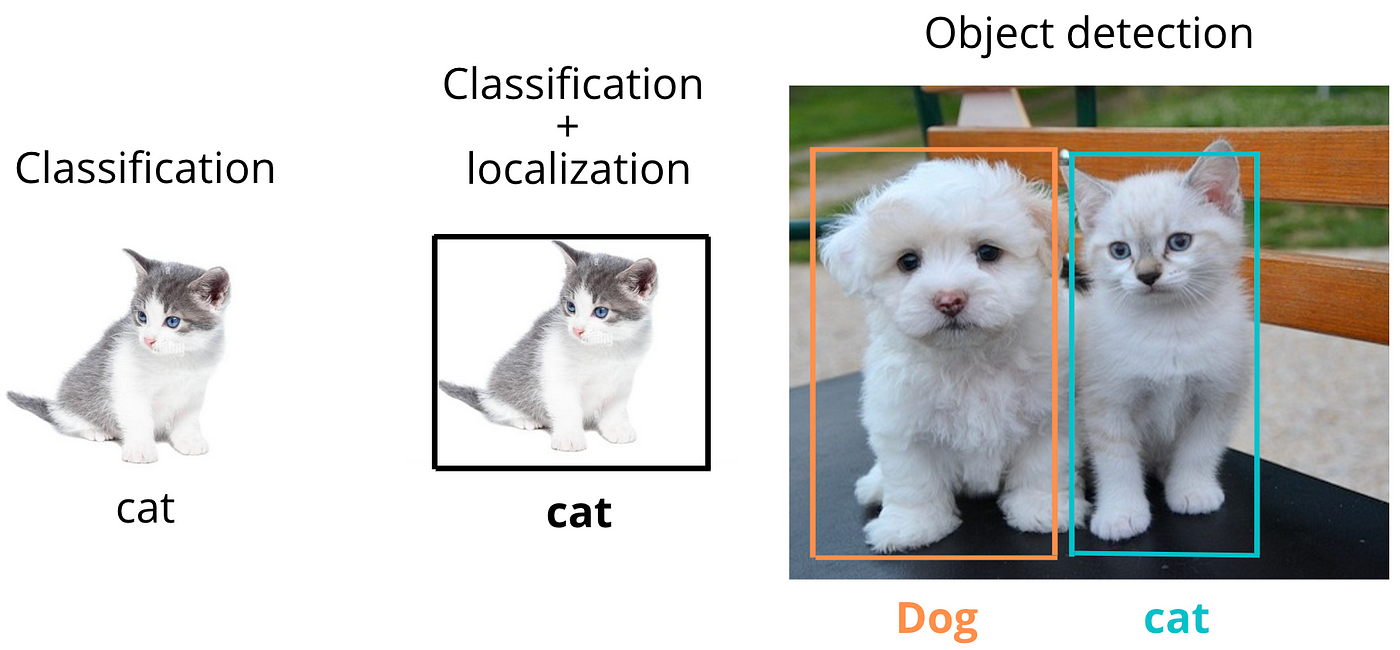
It’s one step more complex than image classification, which only tells what is in the image, not where it is.
Given an image, object localization aims to:
- Classify the object (e.g., cat, dog, car).
- Return the bounding box coordinates around the object:
Where:
- : center of the bounding box
- : width and height of the box
Output Vector
If you're using a neural network for localization, the output vector might be:

Where:
- : Probability that an object exists in the image
- : Bounding box
- : Class probabilities (e.g., cat = 0.8, dog = 0.2)
If the object whose class is defined cannot be detected on the image, will be . In the case where is , the bounding box values () and class values are insignificant in the vector. This means that they are not included when calculating the Loss function.
Loss Function
A multi-part loss is generally used for localization:
- Localization loss (coordinate regression): Measures error in predicted box location
- Confidence loss (objectness): Measures error in object existence
- Classification loss: Measures class prediction error
Example (simplified version as in YOLO):
Landmark Detection
Landmark detection (also called keypoint detection) involves detecting specific key locations on an object. Unlike bounding boxes, keypoints give finer-grained localization.

Example
- Face recognition: Eyes, nose tip, mouth corners
- Hand detection: Fingertips and joints
- Medical imaging: Identifying organ boundaries
Output Representation
If we detect landmarks:
Each pair represents the coordinate of a keypoint like knee point or ear point.
Loss Function
The typical loss for landmark detection:
Object Detection
Object detection combines classification and localization — but now for multiple objects in the same image.
Example
In a single street photo:
- Detect a car (class = car, bounding box)
- Detect a pedestrian (class = human, bounding box)
- Detect a stop sign (class = sign, bounding box)
Compared to Localization
| Task | Output |
|---|---|
| Classification | Class label |
| Localization | Class + bounding box |
| Detection | Multiple classes + boxes |
Model Output Structure
We divide the image into an grid. For each grid cell, predict:
- bounding boxes
- Confidence score
- Class probabilities
Where:
- Each box includes . means this vector.
- : number of classes
Sliding Window Approach and Its Convolutional Implementation
The sliding window technique is a classic method in computer vision used for object detection. The core idea is to take a fixed-size rectangular window and slide it across the input image, systematically checking each region to see whether it contains the object of interest.

At each window position, the cropped image region is passed to a classifier (e.g., SVM, logistic regression, or a small CNN) to determine whether it contains an object. This window "slides" over the image both horizontally and vertically, often with some stride value, producing many cropped regions.
It converts a classification model into a localization tool by brute-force scanning over all possible positions.
Limitations of Naive Sliding Windows
Although conceptually simple, the naive sliding window method has serious drawbacks:
1. High Computational Cost
- For an image of size , using a window of size with stride , the number of windows is: This can result in thousands of regions even for medium-sized images.
- Each window requires a separate forward pass through the classifier network, resulting in massive redundancy since overlapping windows share most of their pixels.
2. Difficulty in Handling Multiple Scales
- Objects in an image can appear at different scales and aspect ratios.
- To address this, either the image must be resized many times or the window size must vary — both of which further increase computation.
3. Fixed Window Shape
- Sliding windows generally use a fixed aspect ratio and size, which makes them less effective for detecting objects with irregular shapes.
Convolutional Implementation of Sliding Windows
To overcome these inefficiencies, modern approaches use the convolutional structure of neural networks to implement the sliding window more efficiently.
Key Insight: Convolutions as Shared Computation
Instead of running the classifier separately on each window, we can:
- Pass the entire image through the convolutional layers of a CNN once
- These layers produce a feature map where each spatial position encodes information about a local receptive field (i.e., a subregion of the image)
- This naturally simulates a sliding window operation
Then, we apply 1x1 convolutions or fully connected layers converted into convolutions over the feature map to produce dense predictions for object presence.
Fully Connected Layer to Convolution
A fully connected layer expecting a flattened input can be rewritten as a 1x1 convolution over a feature map:
- Each position in the resulting output map corresponds to a specific receptive field on the original image
- This effectively implements classification over many regions at once, reusing shared computation
Use in Modern Architectures
Understanding the YOLO (You Only Look Once) Architecture
YOLO (You Only Look Once) is a real-time object detection system that reframes object detection as a single regression problem, rather than a classification or region proposal problem. Instead of scanning the image multiple times or generating multiple proposals, YOLO sees the entire image only once and directly outputs bounding boxes and class probabilities in a single evaluation.
This end-to-end architecture enables extremely fast inference and is designed for real-time applications such as self-driving cars, robotics, surveillance, and augmented reality.
How Does YOLO Work?
At a high level, YOLO divides the input image into a fixed-size grid and makes predictions for each grid cell. Let’s go through each part of the architecture:
1. Image Grid Division
- The input image is divided into an grid (e.g., ).
- Each grid cell is responsible for detecting objects whose center falls inside the cell.
2. Bounding Box Predictions
Each grid cell predicts:
- bounding boxes (typically )
- For each box:
- : coordinates of the box center (relative to the grid cell)
- : width and height of the box (relative to the whole image)
- : confidence score =
3. Class Probabilities
-
Each grid cell also predicts conditional class probabilities:
-
These probabilities are class probabilities conditioned on the presence of an object in the cell.
4. Final Predictions
- The total output per grid cell is: For example, with , , , the total prediction tensor size is:
Why Is It Called “You Only Look Once”?
Traditional detection pipelines involve:
- Generating region proposals (like in R-CNN)
- Running a CNN on each region
- Performing classification and box regression separately
YOLO unifies this pipeline into a single CNN pass, hence the name “You Only Look Once”. The model sees the full image context and outputs all bounding boxes and class scores in one go.
SSD (Single Shot MultiBox Detector)
- Detects objects at multiple scales using feature maps from different layers
- Uses convolutional layers to predict class and box offsets at every location in the feature map
Summary
| Approach | Characteristics |
|---|---|
| Naive Sliding Window | Slow, inefficient, redundant computation |
| Convolutional Sliding | Efficient, shared computation, suitable for real-time detection |
By understanding this transition from brute-force scanning to convolutional prediction, we appreciate how convolutional networks not only recognize what is in an image but also where, enabling scalable object detection.
Evaluation and Optimization: IoU, Non-max Suppression, Anchor Boxes
Intersection over Union (IoU)
Intersection over Union (IoU) is a metric used to evaluate the accuracy of an object detector on a particular dataset. It measures the overlap between two bounding boxes:
- The predicted bounding box
- The ground-truth bounding box
Mathematical Definition
If is the predicted bounding box and is the ground truth bounding box:
- : perfect overlap
- : no overlap
Example
Suppose:
- Predicted box: top-left = (50, 50), bottom-right = (150, 150)
- Ground truth: top-left = (100, 100), bottom-right = (200, 200)
The overlapping area is a square from (100, 100) to (150, 150) → 50x50 = 2500
Total area:
- Predicted:
- GT:
- Union:
So,
Use in Training and Evaluation
- In training, you may ignore detections with IoU < 0.5
- For evaluation, mAP (mean average precision) uses IoU thresholds (e.g., 0.5 or 0.75)
Non-max Suppression (NMS)
Why Do We Need It?
Object detectors often output multiple overlapping boxes for a single object. NMS filters out redundant boxes by keeping the one with the highest confidence score.
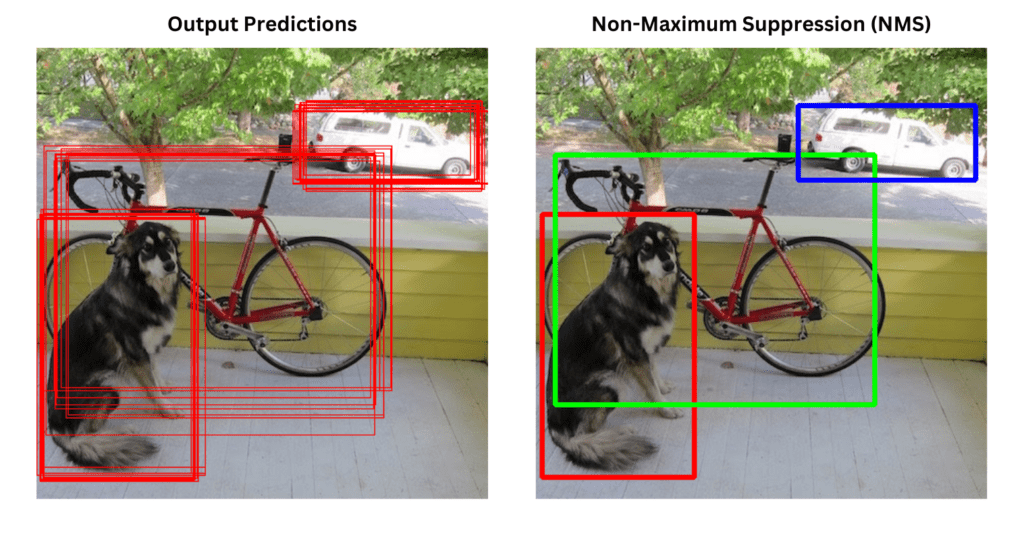
Algorithm Steps
- Sort all bounding boxes by their confidence score.
- Select the box with the highest confidence and remove it from the list.
- Compute IoU between this box and all others.
- Remove boxes with IoU above a threshold (e.g., 0.5).
- Repeat until no boxes remain.
Mathematical Intuition
Let be a box with score . You iterate over all boxes and apply:
Where is the suppression threshold.
Anchor Boxes
What are Anchor Boxes?
Anchor boxes (also called prior boxes) are predefined bounding boxes with different shapes and sizes. They allow object detectors to:
- Detect multiple objects in the same grid cell
- Handle aspect ratio and scale variation
Why Are They Needed?
Without anchor boxes, a single grid cell could detect only one object. But real-world scenes often contain overlapping or closely spaced objects.
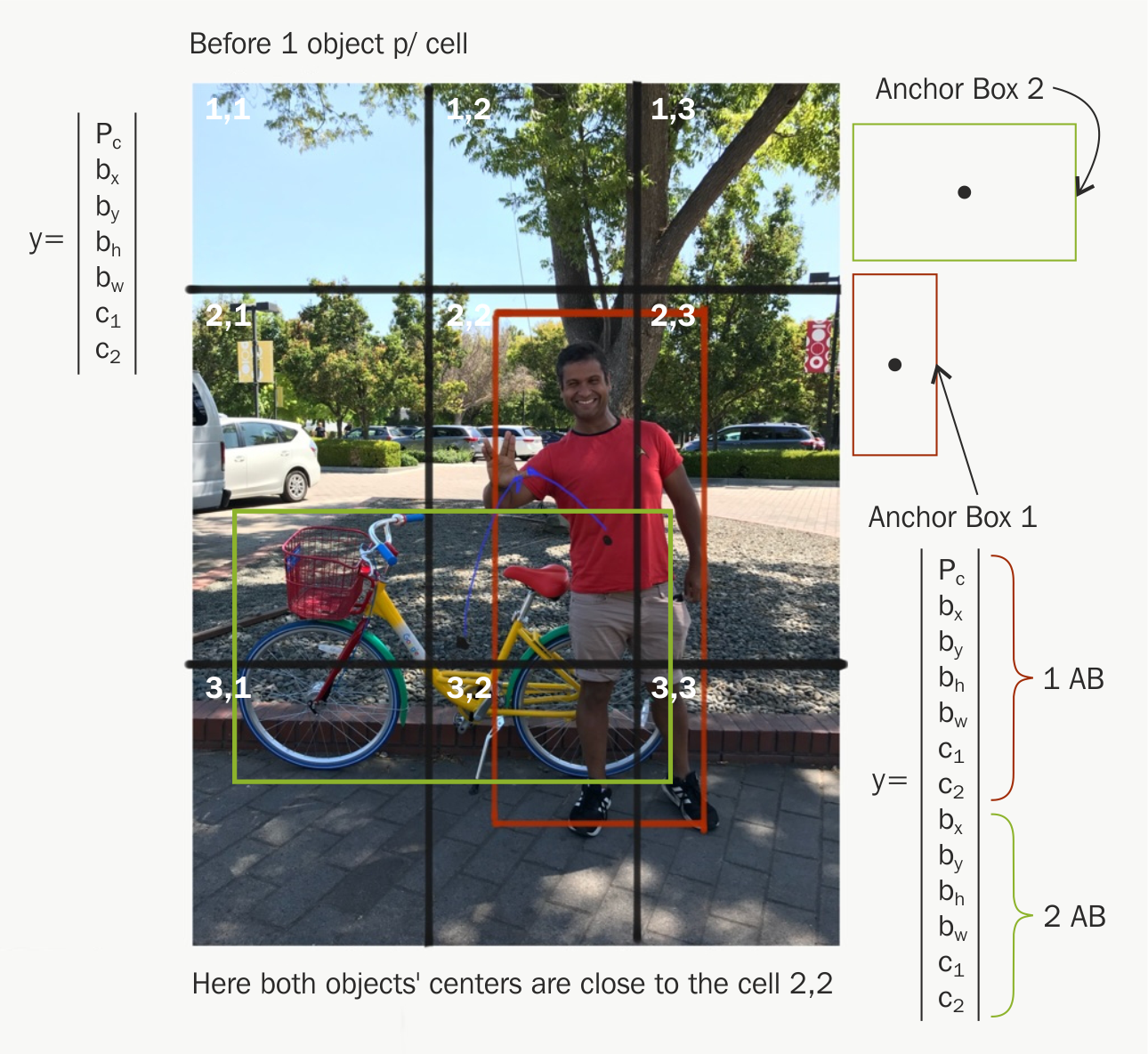
Anchor Box Design
You predefine anchor boxes per cell. Each one is defined by:
- Width
- Height
- Aspect ratio
For example, in SSD:
- 3 feature maps
- 6 anchors per feature cell
- 8732 total anchor boxes
Output Format with Anchors
For each anchor box, the network predicts:
- : offset from anchor center
- : log scale changes to width and height
- Confidence score
- Class probabilities
This transforms anchor box to the predicted box :
Summary
- IoU measures overlap and is used for loss/evaluation.
- Non-max suppression removes redundant boxes based on IoU.
- Anchor boxes allow detection of multiple objects at different scales/aspect ratios.
Together, these techniques form the foundation of modern object detection pipelines like YOLO, SSD, and Faster R-CNN.
Region Proposals and Semantic Segmentation: U-Net
- Region Proposals
- Semantic Segmentation
- Transpose Convolutions (Deconvolution)
- U-Net Architecture Intuition
- U-Net Architecture (Full Design)
- Summary
Region Proposals
Why Region Proposals?
Traditional object detectors like sliding windows are computationally expensive due to scanning every possible region in the image. Region Proposal methods address this by generating a small number of candidate regions likely to contain objects.
Selective Search

- Group similar pixels into superpixels
- Merge regions based on similarity
- Outputs ~2000 proposals per image
R-CNN Pipeline
- Use Selective Search to propose regions.
- Warp each region to a fixed size (e.g., 224x224).
- Pass through a ConvNet to extract features.
- Use SVMs for classification and regressors for bounding boxes.
Limitation: Very slow due to independent ConvNet run on each region.
Semantic Segmentation
What is Semantic Segmentation?
Semantic segmentation is the task of classifying each pixel of an image into a class label.
- Image Classification: What is in the image?
- Object Detection: Where is the object?
- Semantic Segmentation: Which pixel belongs to which class?
Applications
- Medical imaging (e.g., tumor segmentation)
- Autonomous driving (lane and pedestrian detection)
- Satellite image analysis
- Industrial defect detection
Transpose Convolutions (Deconvolution)
Motivation
In segmentation tasks, we need to upsample feature maps back to the original image size. Transpose convolutions (a.k.a. deconvolutions) help with this.
How It Works
A transpose convolution is the reverse of a normal convolution:
- While convolution reduces spatial size (downsampling),
- Transpose convolution increases it (upsampling).
Mathematical Operation
Suppose an input size of and a kernel size of with stride .
-
Convolution output size:
-
Transpose convolution (reverses the above):
Alternatives
- Nearest-neighbor or bilinear upsampling + 1x1 conv (cheaper, less expressive)
- Learned transpose convolutions (richer)
U-Net Architecture Intuition
Key Idea
U-Net is a fully convolutional network that consists of:
- A contracting path to capture context (downsampling)
- An expanding path to enable precise localization (upsampling)
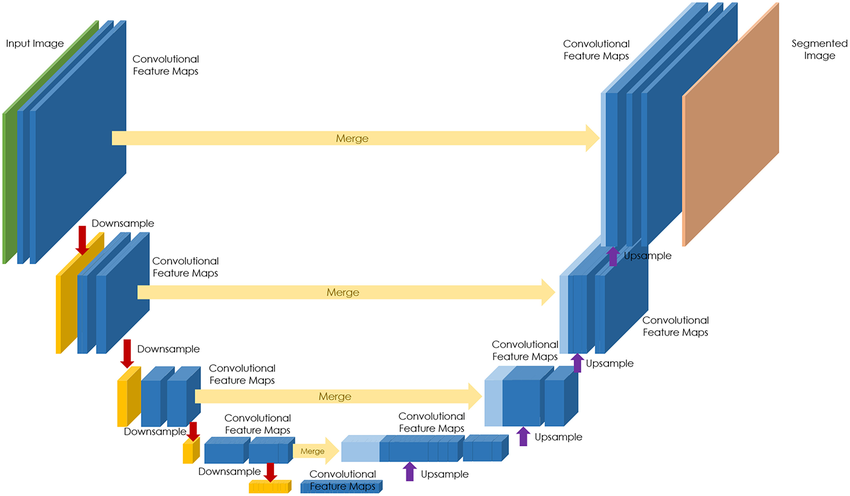
U-Net was originally designed for biomedical image segmentation but is now used in many fields.
Contracting Path (Encoder)
- Similar to standard CNN (e.g., VGG)
- Repeated 2x:
- Conv (ReLU) → Conv (ReLU) → MaxPooling
Expanding Path (Decoder)
- Transpose convolution for upsampling
- Skip connections concatenate features from encoder
Why Skip Connections?
Skip connections pass high-resolution features from encoder to decoder, enabling:
- Better boundary localization
- Preservation of fine details
U-Net Architecture (Full Design)
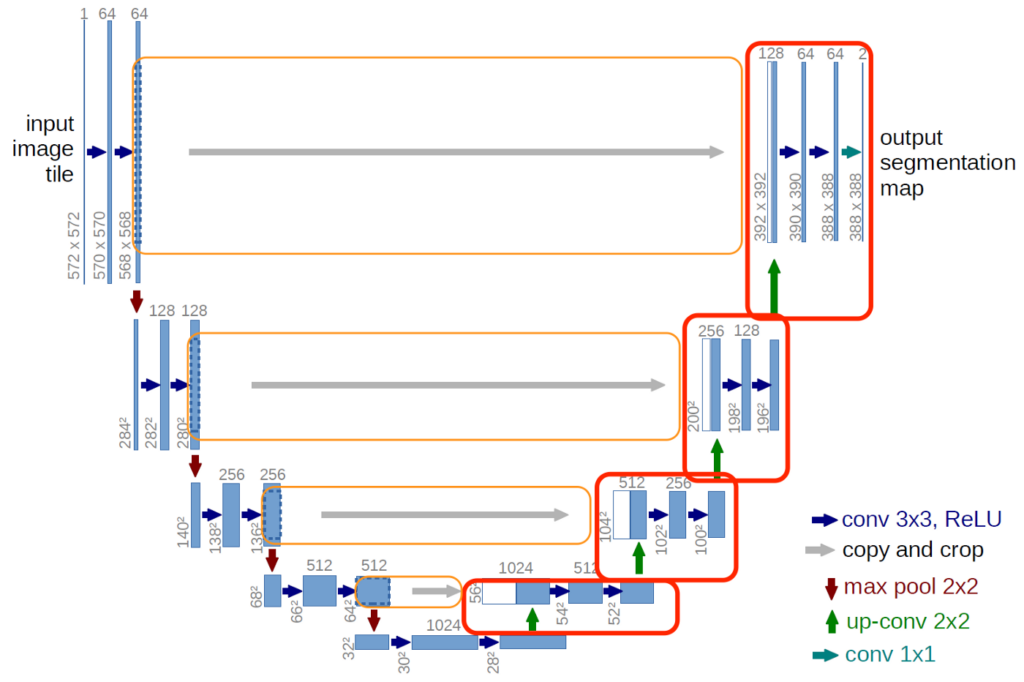
Structure Overview
- Input size:
- Each layer: two convolutions + ReLU
- Downsampling: max-pooling
- Upsampling: transpose convolutions
- Final output: convolution to map to classes (per pixel)
Example Architecture
Input → Conv → Conv → Pool
↓ ↑
Conv → Conv → Pool
↓ ↑
Conv → Conv → Pool
↓ ↑
Bottleneck ← Skip Connections
↓ ↑
Upconv → Concat → Conv → Conv
↓
Output (Segmentation Map)
Loss Function
Typical loss: Pixel-wise cross-entropy loss.
Where:
- : height and width of the image
- : number of classes
- : ground truth indicator (1 if pixel belongs to class )
- : predicted probability for class at pixel
Performance Metrics
- Pixel Accuracy: overall correct classification
- IoU per class: same as object detection, applied per-pixel
- Dice Coefficient: common in medical segmentation
Summary
- Region proposals are key to efficient object detection pipelines like R-CNN.
- Semantic segmentation classifies each pixel and requires upsampling layers.
- Transpose convolutions allow learned upsampling.
- U-Net combines low-level and high-level features through skip connections and is state-of-the-art for many segmentation tasks.
Face Recognition and Neural Style Transfer
What is Face Recognition?
Face recognition is the task of identifying or verifying a person’s identity using their facial features. It can be broken down into three main categories:
- Face Detection: Locate faces in an image (bounding box).
- Face Verification: Check if two faces are of the same person (1:1 comparison).
- Face Recognition/Identification: Identify a person from a database (1:N comparison).
Real-World Applications
- Smartphone unlock (Face ID)
- Security surveillance
- Online proctoring
- Social media tagging (e.g., Facebook)
One Shot Learning
Traditional classification algorithms require many training examples per class. However, in face recognition:
- We might only have one image per person.
- The task becomes: Can the model recognize a face it has seen only once?
This is known as One-Shot Learning.
Problem Setup
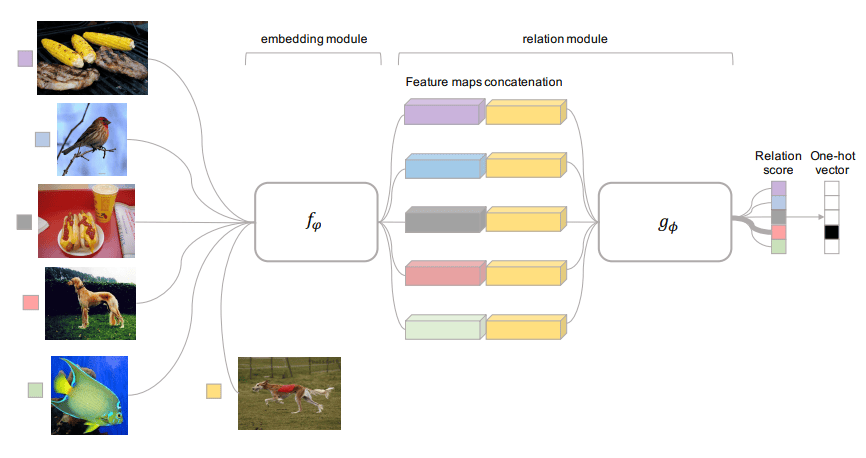
- Instead of learning to classify, the model learns similarity between pairs of images.
- A distance function is trained to return a small value for the same person, and large for different people.
Siamese Network
A Siamese Network consists of two identical ConvNets (with shared weights) that compare two inputs.
Architecture Overview
- Two inputs: and
- Same CNN maps both to feature vectors and
- A distance metric (e.g., L2 norm) is applied:
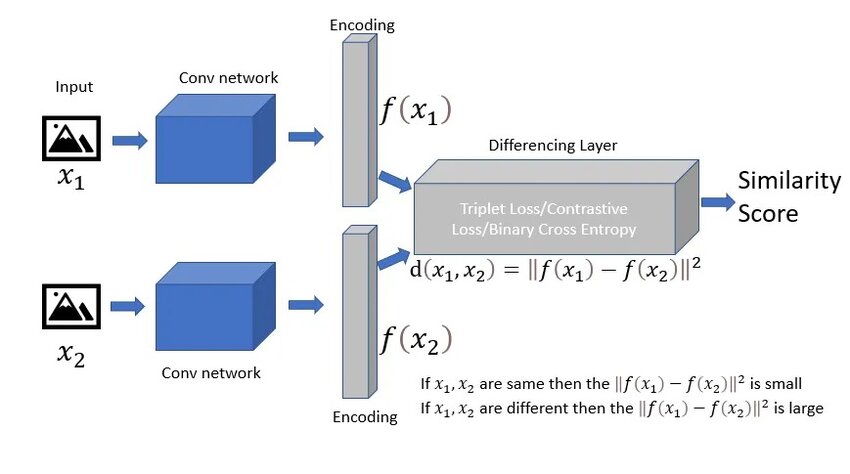
Loss Function
A contrastive loss or triplet loss is used to train the network to minimize distances for same identities and maximize for different ones.
Triplet Loss
Triplet Loss is a powerful loss function for learning embeddings. It relies on triplets:
- Anchor (A): A known image
- Positive (P): Image of the same identity
- Negative (N): Image of a different identity
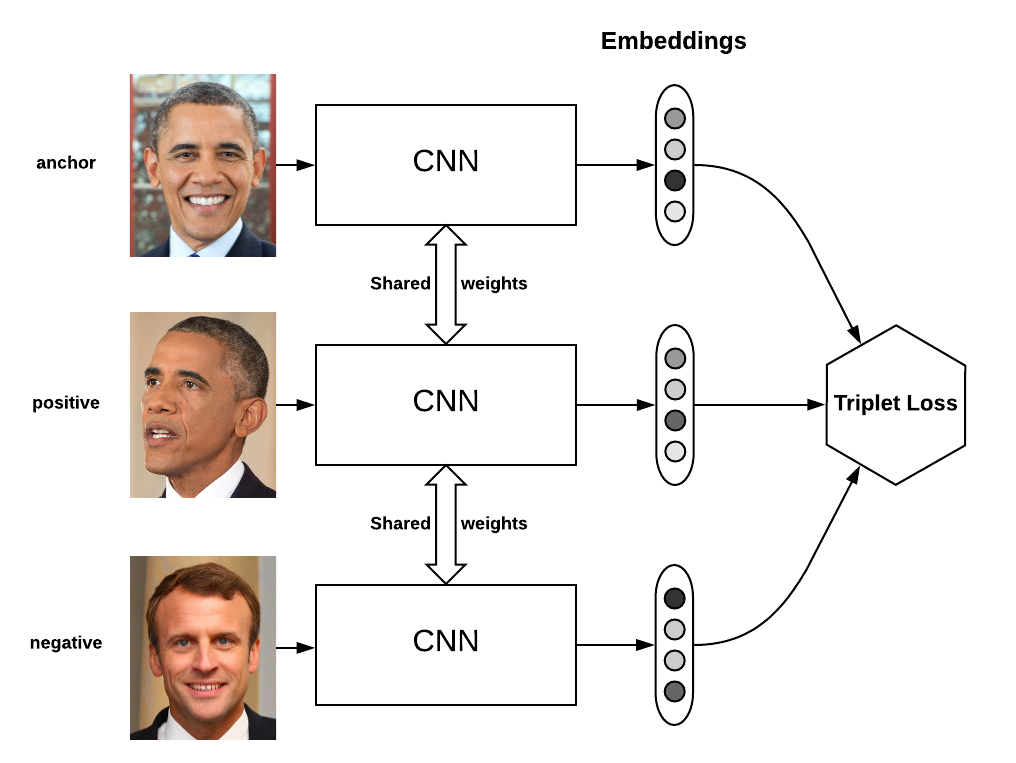
We want:
Where:
- is the embedding function (ConvNet output)
- is a margin to separate positive and negative pairs
Loss Function
The Triplet Loss is:
Important Notes
- Semi-hard negative mining improves convergence (choose negatives that are hard but not too hard).
- Embeddings are often normalized to unit length.
Face Verification and Binary Classification
Once we have embeddings from a trained network (e.g., using triplet loss), we can perform face verification as a binary classification task.
Verification Pipeline
- Encode both face images to embeddings.
- Compute Euclidean distance or cosine similarity.
- If distance < threshold same person.
Threshold is selected based on False Positive Rate vs. True Positive Rate using ROC curve on a validation set.
What is Neural Style Transfer?
Neural Style Transfer is the task of synthesizing an image that:
- Preserves the content of a content image
- Adopts the style of a style image
Leverage a pre-trained ConvNet (like VGG19) to extract content and style representations.
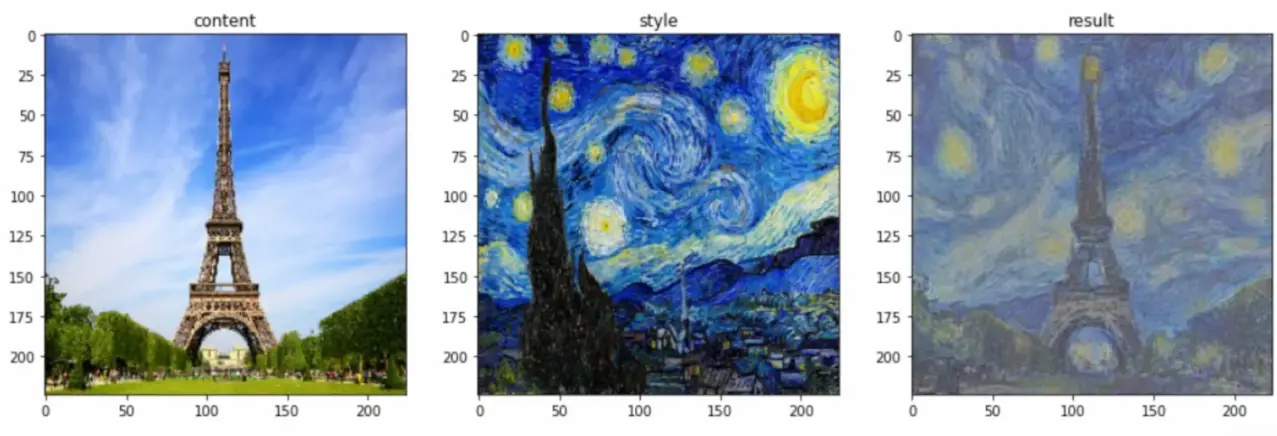
Let:
- be the content image
- be the style image
- be the generated image
Then we optimize to minimize a cost function:
What are Deep ConvNets Learning?
Deep ConvNets learn hierarchical representations:

- Early layers: edges, colors, textures
- Mid layers: shapes, motifs
- Later layers: object-level concepts
In NST, content is encoded in deeper layers, style in shallower layers.
Cost Function
The total cost is:
Where:
- : weight for content preservation
- : weight for style transfer
- Typically: , to
Content Cost Function
Let and be activations at layer for the content and generated images.
Then content cost is:
Use a deeper layer (e.g., conv4_2) for this.
Style Cost Function
Style is captured by correlations between feature maps using a Gram matrix.
Let be the activations at layer for style image. Compute Gram matrix:
Style cost is:
Then sum over multiple layers:
1D and 3D Generalizations
1D Generalization
Neural style transfer principles can be applied to audio signals:
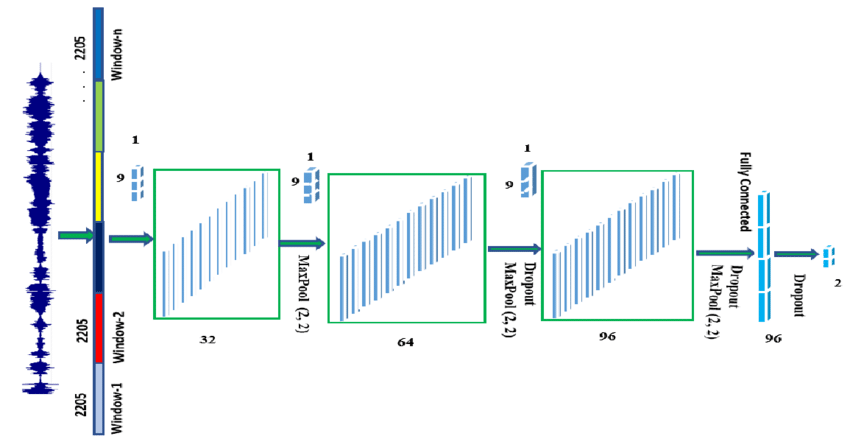
- 1D convolution over waveform
- Preserve temporal content, apply style of another sound
3D Generalization
Applied to volumetric data such as:
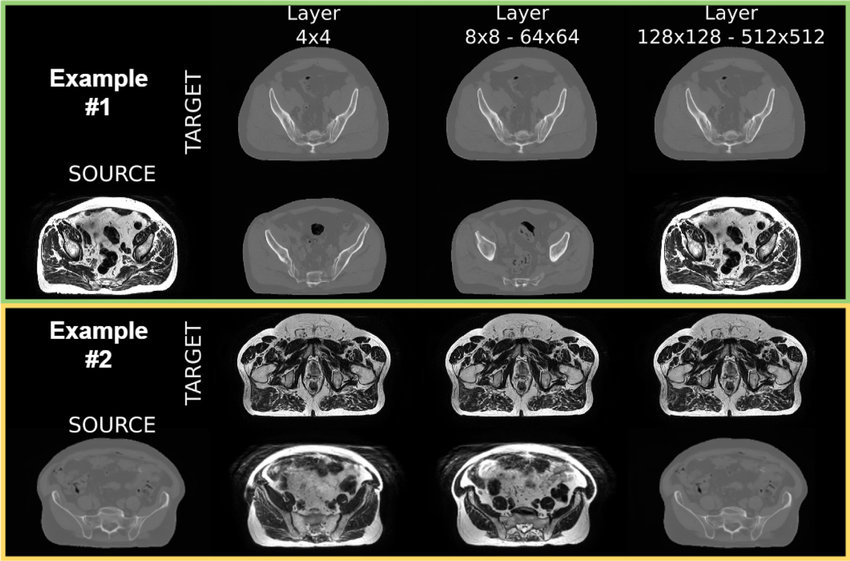
- 3D MRI scans
- 3D point clouds
- Transfer spatial styles across 3D volumes
These require 3D convolutional layers and custom Gram matrix calculations.
Summary
- Face Recognition uses embedding learning (Triplet loss, Siamese networks).
- One-shot learning enables models to generalize with limited data.
- Neural Style Transfer uses a pre-trained CNN to blend content and style images using a combination of content/style loss.
- Both applications showcase the expressive power of deep convolutional networks beyond classic classification.
Recurrent Neural Networks (RNNs)
- Why Sequence Models?
- Notation
- Recurrent Neural Network Model
- Backpropagation Through Time
- Different Types of RNNs
- Language Model and Sequence Generation
- Sampling Novel Sequences
- Vanishing Gradients with RNNs
- Gated Recurrent Unit (GRU)
- Long Short-Term Memory (LSTM)
- Bidirectional RNN
- Deep RNNs
Why Sequence Models?
Sequence models are used when the input and/or output is sequential. For example:
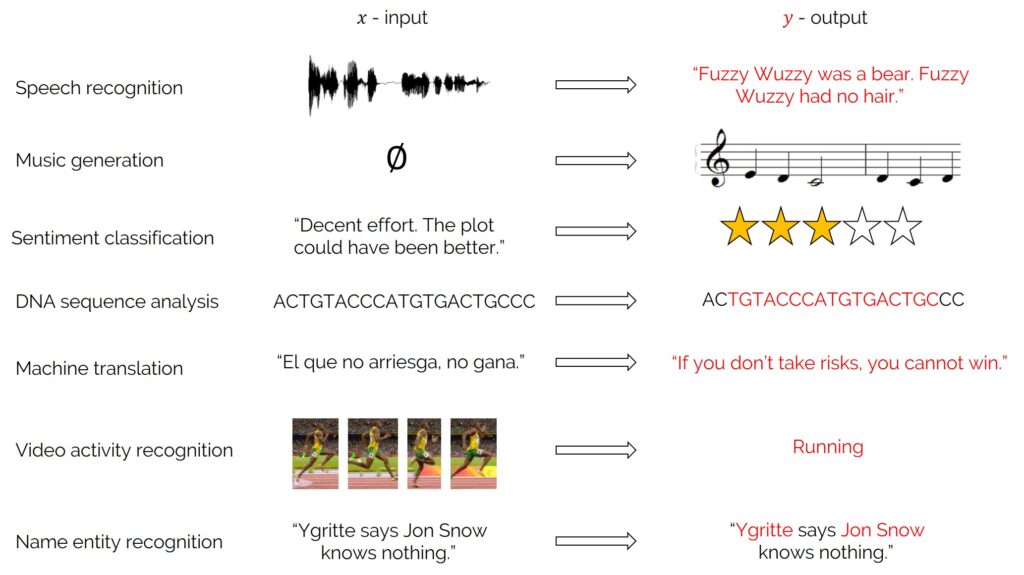
They model dependencies over time or sequence positions, which standard feedforward neural networks cannot do efficiently.
Notation
- : input at time step
- : output at time step
- : hidden state at time step
- : predicted output at time step
- : sequence length
Recurrent Neural Network Model
The RNN computes:
RNNs share parameters across time, allowing generalization to different sequence lengths.
Backpropagation Through Time
To train RNNs, we use backpropagation through time (BPTT):
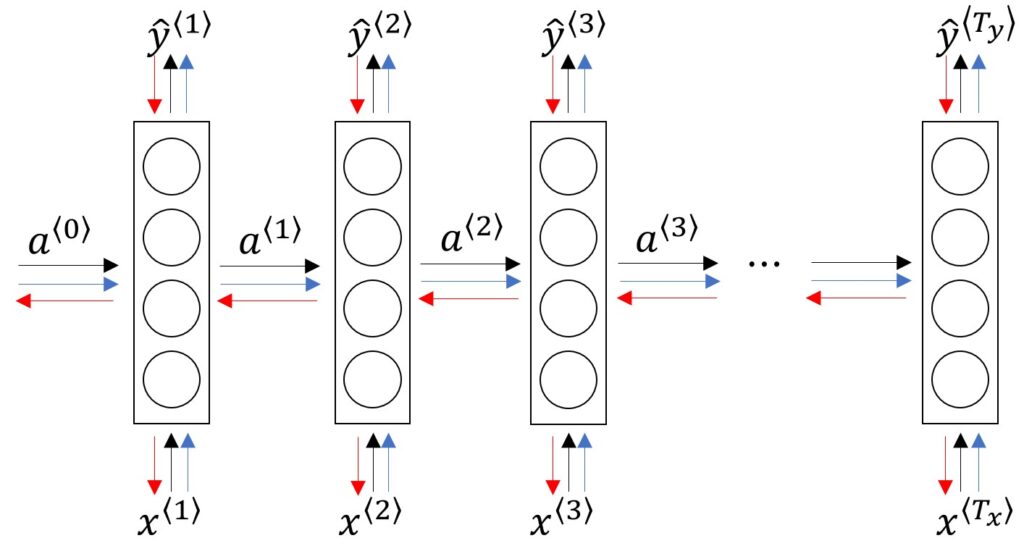
- Unroll the RNN for steps
- Compute loss and gradients across all time steps
- Apply chain rule for gradients through time dependencies
Different Types of RNNs
- Many-to-Many: sequence input and sequence output (e.g., machine translation)
- Many-to-One: sequence input, single output (e.g., sentiment analysis)
- One-to-Many: single input, sequence output (e.g., image captioning)
Language Model and Sequence Generation
Language models predict the next word given a sequence:
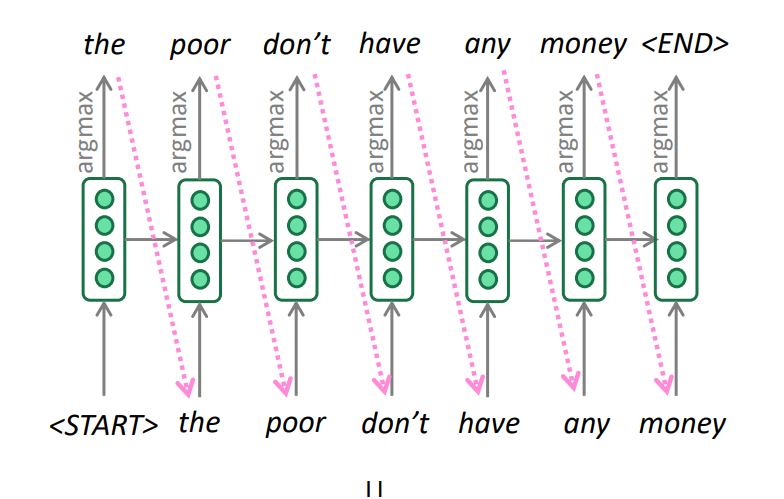
Training: minimize cross-entropy loss between predicted and actual next words.
Sampling Novel Sequences
- Start with a seed (e.g.,
) - Sample , feed it back
- Continue until
or max length
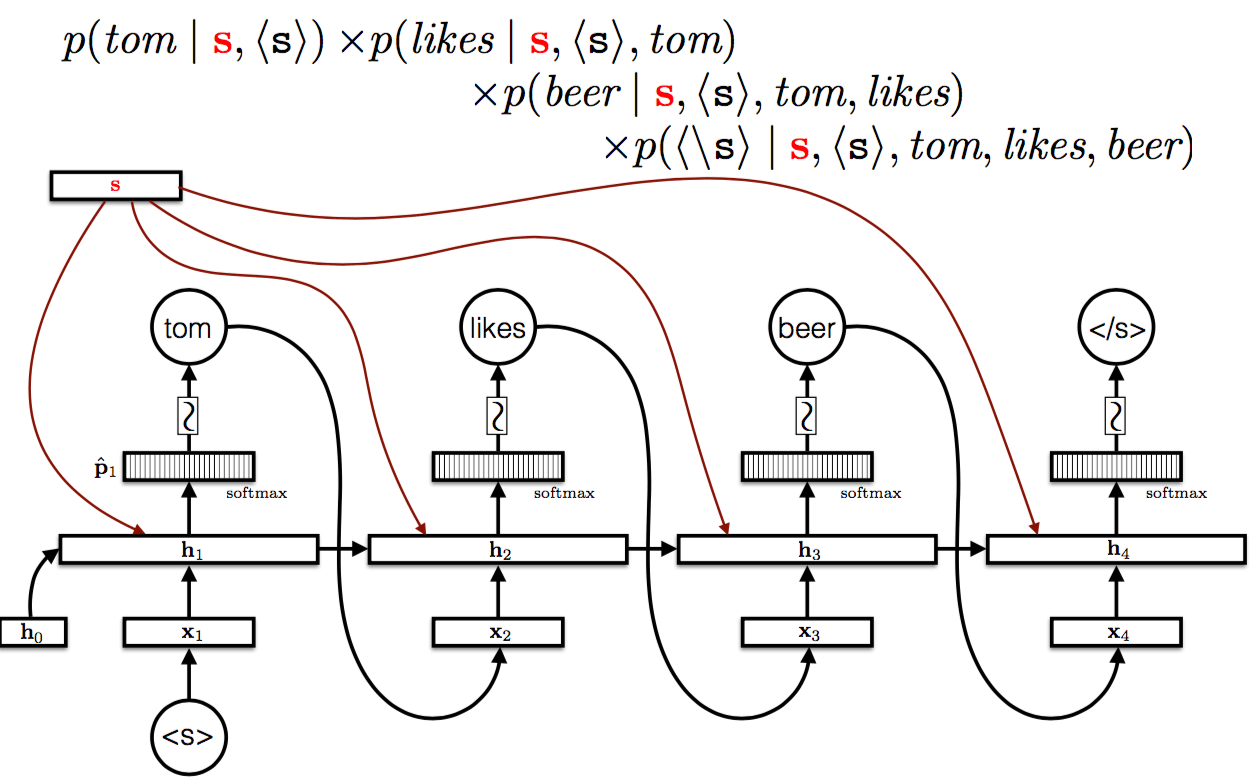
Sampling temperature can control randomness:
- Low temperature = conservative (likely choices)
- High temperature = creative (diverse outputs)
Vanishing Gradients with RNNs
One of the fundamental challenges in training RNNs is the vanishing gradient problem, especially when modeling long-term dependencies.
When computing gradients using Backpropagation Through Time (BPTT), the gradients at earlier time steps are affected by the repeated multiplication of small values (from derivatives of activation functions like tanh or sigmoid). This leads to:
- Gradients becoming very small (vanish): weights are barely updated for earlier time steps
- Gradients becoming very large (explode): instability and divergence in training
Intuition with Example:
Consider a sequence: "I grew up in France... I speak fluent ___"
The model needs to learn that the word "French" depends on the context word "France" seen many time steps earlier. If the gradient shrinks too much over those steps, the model fails to learn this dependency.
Consequences:
- Short-term dependencies are learned effectively.
- Long-term dependencies are often lost.
Gated Recurrent Unit (GRU)
Why do we need GRUs?
Traditional RNNs struggle with learning long-term dependencies due to the vanishing gradient problem. As sequences grow longer, the gradients used during backpropagation either shrink or explode, making it hard for the network to retain information over time.
GRUs are designed to solve this by introducing gating mechanisms that control what information should be remembered, updated, or forgotten. These gates make the network more efficient at learning dependencies in long sequences.
GRU introduces gates to control information flow:
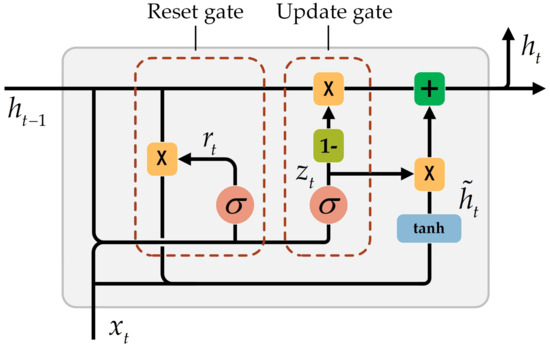
A GRU has two main gates:
-
Update Gate ():
-
Determines how much of the previous memory to keep.
-
If z ≈ 1, it keeps the old memory.
-
If z ≈ 0, it updates with new information.
-
-
Reset Gate ():
-
Controls how much of the previous state should be ignored.
-
Helps in deciding whether to forget the old state when generating the new memory.
-
Equations:
GRU vs Traditional RNN
| Feature | RNN | GRU |
|---|---|---|
| Memory control | None | Yes (update/reset gates) |
| Vanishing gradients | Common | Less frequent |
| Parameter efficiency | Fewer params | More, but fewer than LSTM |
| Training speed | Fast | Slower than RNN, faster than LSTM |
Example: Sequence with Context
Imagine trying to classify the sentiment of the sentence:
“The movie was terrible... but the ending was amazing.”
- A vanilla RNN might forget the earlier "terrible" and overly weight the "amazing", resulting in an incorrect positive classification.
- A GRU, however, can learn to retain both sentiments and give a more balanced representation by preserving long-term context.
Long Short-Term Memory (LSTM)
Why Do We Need LSTM?
Traditional RNNs struggle with long-term dependencies due to vanishing gradients, which hinder learning over long sequences.
To solve this, LSTMs introduce memory cells and gates that help preserve and regulate information across time steps.
LSTM Architecture Intuition
LSTM cells introduce three gates to control information:
- Forget Gate: Decides what information to throw away from the cell state.
- Input Gate: Decides which new information should be stored in the cell state.
- Output Gate: Decides what to output based on the cell state.
This gating mechanism allows the model to retain relevant information over long durations while discarding unnecessary data.
LSTM Cell: Step-by-Step
Let’s break down an LSTM cell computation for a single time step . Let:
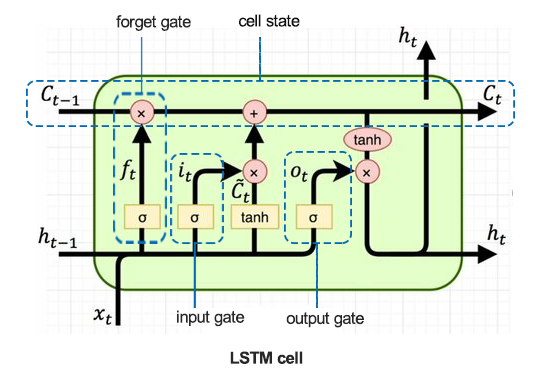
- : input at time
- : hidden state from previous step
- : cell state from previous step
Then, the LSTM performs the following operations:
-
Forget Gate :
Decides what to forget from the previous cell state.
-
Input Gate and Candidate Values :
Determines what new information to add to the cell state.
-
Update Cell State:
-
Output Gate and Hidden State :
Example: Comparing RNN and LSTM
Suppose we want to predict the next word in a sentence. Let’s compare:
RNN:
- Struggles to maintain context when sentences are long.
- For example:
"The cat, which was chased by the dog, ran up the..." → "tree"→ the subject "cat" may be forgotten.
LSTM:
- Maintains the context of "the cat" and successfully predicts
"tree".
| Feature | RNN | LSTM |
|---|---|---|
| Handles Long-Term Dependencies | ❌ | ✅ |
| Vanishing Gradient Resistant | ❌ | ✅ |
| Uses Gates | ❌ | ✅ (Forget, Input, Output) |
| Computational Complexity | Low | Higher, but more expressive |
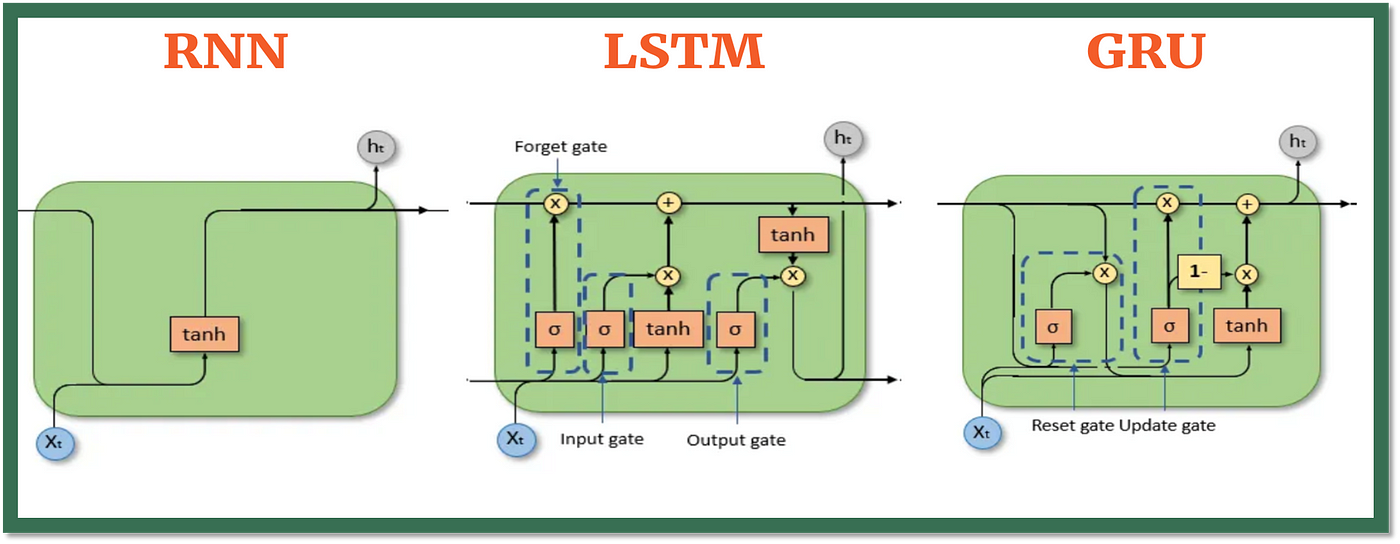
LSTMs are widely used in natural language processing, speech recognition, time series forecasting, and anywhere long-term memory is crucial.
Bidirectional RNN
In a standard RNN, information flows in a single direction — typically from past to future. However, in many tasks (like speech recognition or named entity recognition), context from both past and future words is useful for understanding the current input. This is where Bidirectional RNNs (BiRNNs) come in.
Why Use Bidirectional RNNs?
A Bidirectional RNN processes the input sequence in both directions with two separate hidden layers:
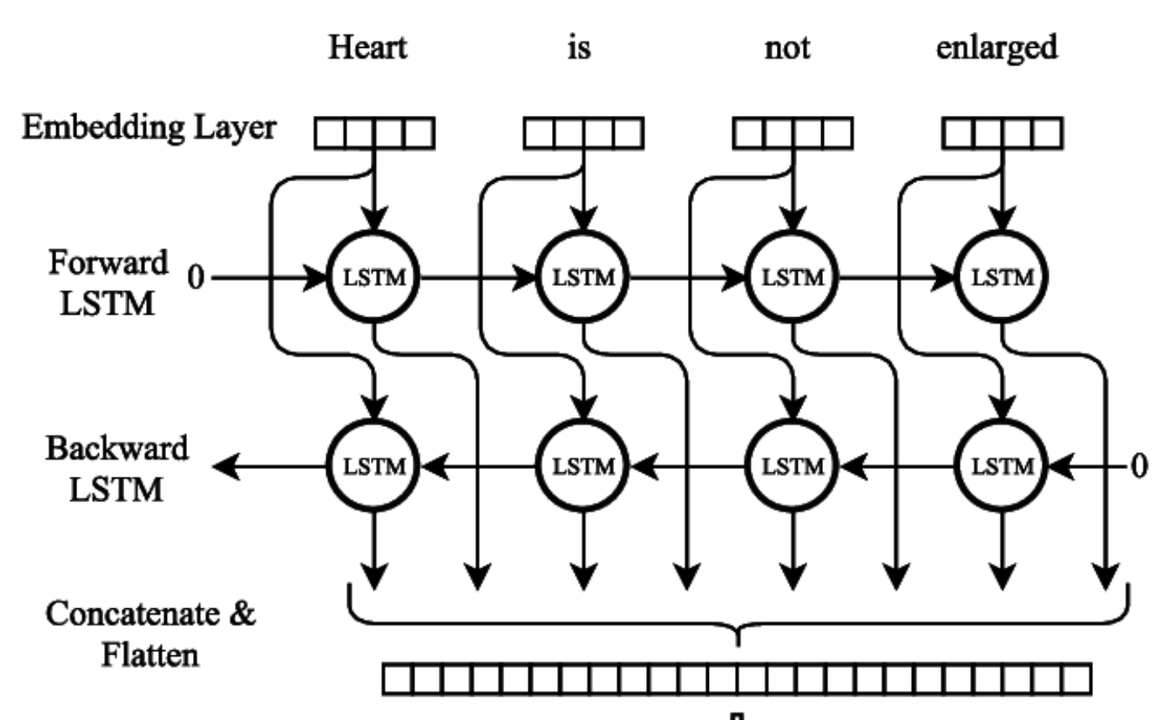
- One moves forward through time (from to )
- One moves backward through time (from to )
The outputs of both directions are concatenated at each time step:
- Access to future context: Helps the model make better predictions at each time step.
- Improved performance: Especially effective in tasks where the meaning of a word depends on both previous and next words.
Imagine the sentence:
"He said he saw a bat."
If we only process the sentence from left to right, the meaning of the word "bat" is unclear until we see the following context. A Bidirectional RNN can process both directions and better disambiguate the meaning using the full sentence context.
Applications
- Named Entity Recognition (NER)
- Part-of-Speech (POS) tagging
- Speech recognition
- Text classification
Bidirectional RNNs are often used with LSTM or GRU units to capture long-term dependencies more effectively in both directions.
Deep RNNs
Deep RNNs consist of stacking multiple recurrent layers on top of each other, allowing the network to learn hierarchical representations of sequences. By increasing the depth, the model can capture more complex temporal patterns and abstractions.
- Each layer’s output serves as input to the next recurrent layer.
- Enables learning of higher-level features across time steps.
- Can improve model capacity and expressiveness.
Challenges:
- Increased risk of overfitting due to more parameters.
- Training can be slower and more difficult due to vanishing/exploding gradients.
Applications:
- Complex sequence modeling tasks such as speech recognition, language modeling, and video analysis.
Deep RNNs are often combined with advanced units like LSTM or GRU to mitigate training difficulties and capture long-term dependencies effectively.
Natural Language Processing and Word Embeddings
- Word Representation
- Using Word Embeddings
- Properties of Word Embeddings
- Embedding Matrix
- Learning Word Embeddings
- Word2Vec
- Negative Sampling
- GloVe Word Vectors
- Sentiment Classification
- Debiasing Word Embeddings
Word Representation
In Natural Language Processing (NLP), word representation refers to how words are converted into a numerical form that a machine learning model can understand. Traditional approaches used one-hot encoding, where each word is represented by a binary vector of the vocabulary size. However, one-hot vectors suffer from high dimensionality and no semantic information.
Example:
This image shown one-hot embedding example.
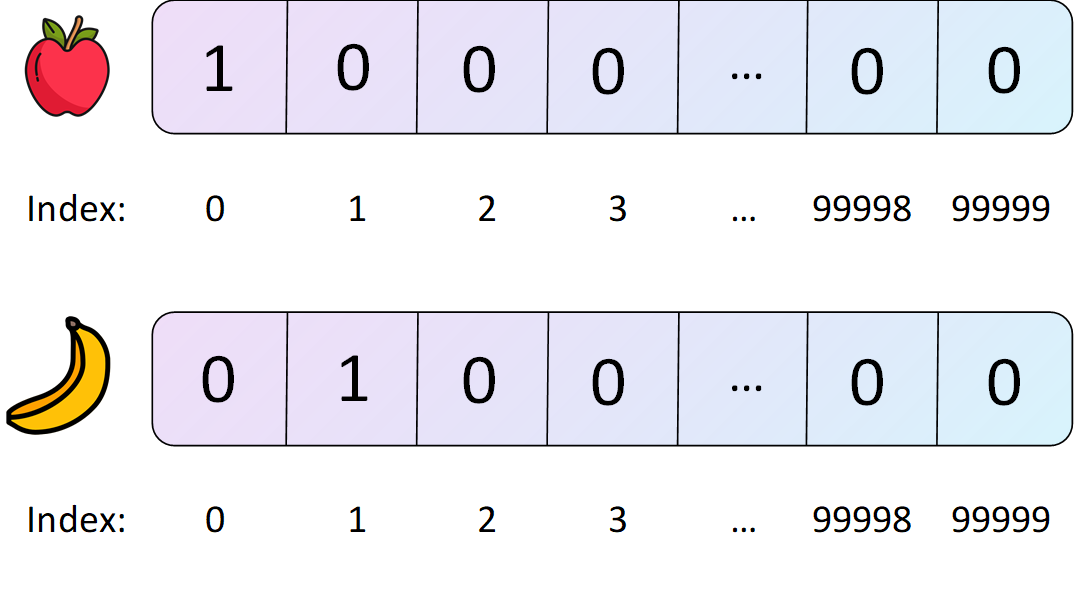
Vocabulary: ["king", "banana", "apple"]
One-hot representation of "king": [1, 0, 0]
One-hot representation of "banana": [0, 1, 0]
One-hot representation of "apple": [0, 0, 1]
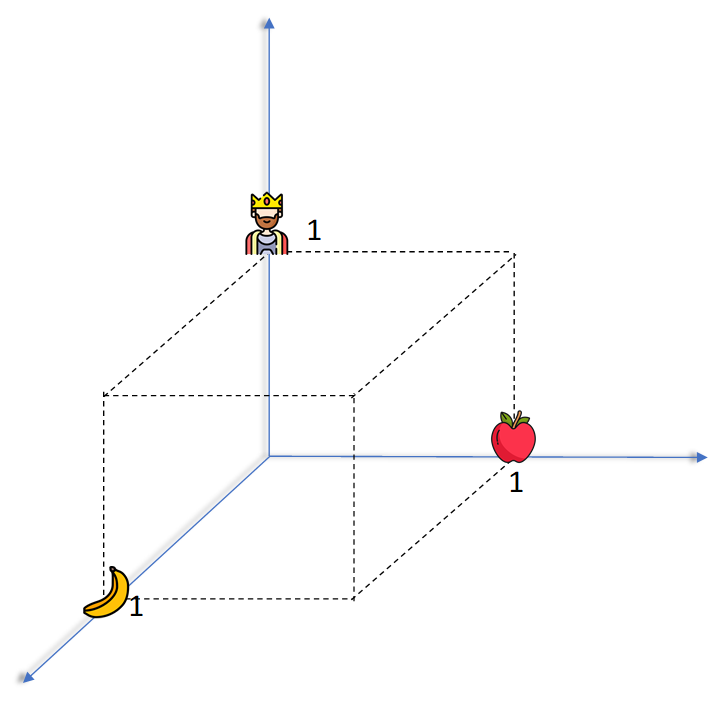
This representation doesn't capture the relationship between "banana" and "apple" or that both are fruit. Hence, we need better methods like word embeddings.
Using Word Embeddings
Word embeddings are dense vector representations of words in a continuous vector space, where semantically similar words are mapped closer together.

Example: A 3D visualization might show vectors such that:
- vector("king") - vector("man") + vector("woman") ≈ vector("queen")
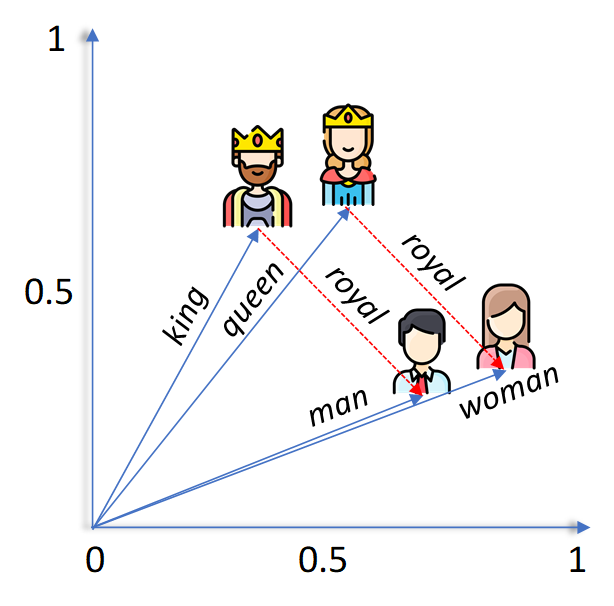
This arithmetic reflects the semantic relationship between the words, allowing machines to understand analogies.
Properties of Word Embeddings
Word embeddings exhibit fascinating properties:
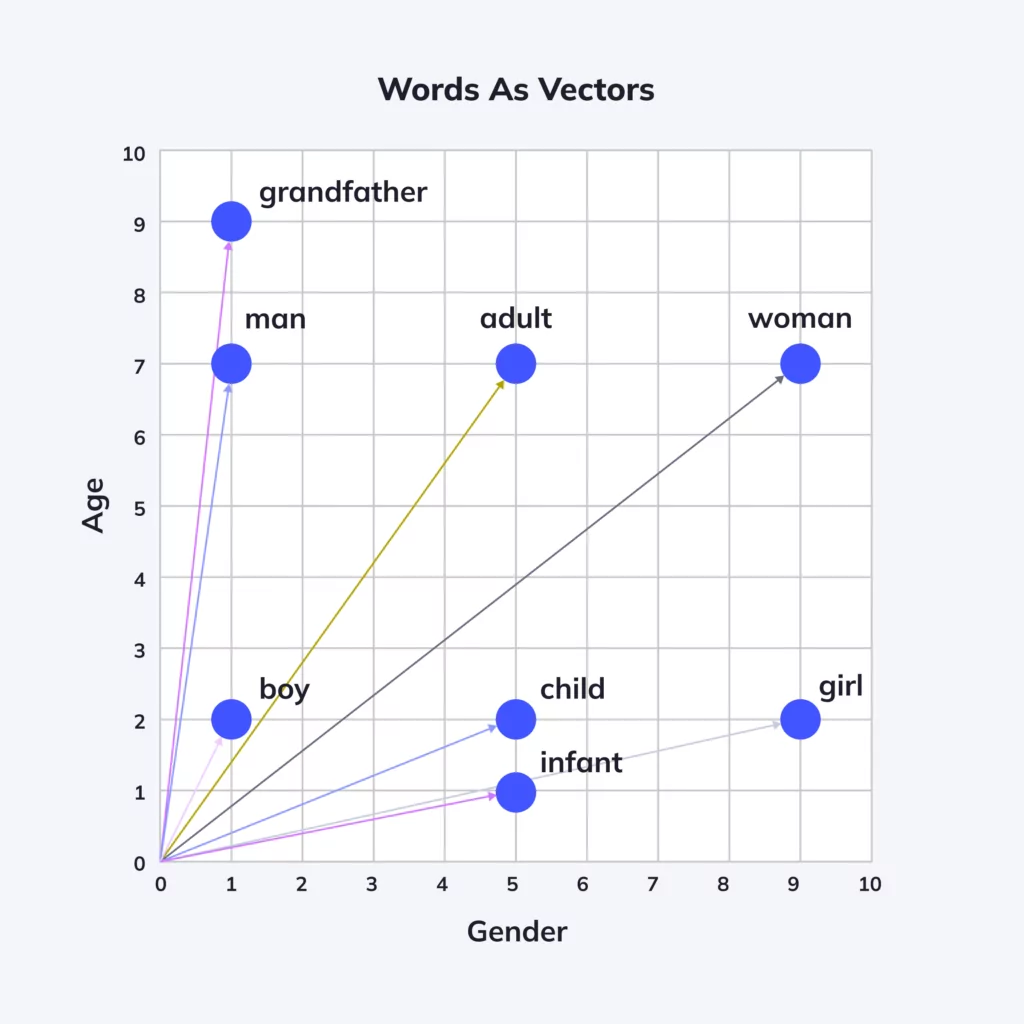
- Semantic similarity: Similar words have vectors close to each other (e.g., "good" and "great").
- Linear substructures: Relationships can be captured with simple vector arithmetic (e.g., "Paris" - "France" + "Italy" ≈ "Rome").
- Dimensionality reduction: Embeddings reduce high-dimensional one-hot vectors to lower-dimensional dense vectors (e.g., from 10,000 to 300 dimensions).
Embedding Matrix
An embedding matrix is a trainable matrix in a neural network where each row corresponds to a word’s vector.
Structure:
- Suppose the vocabulary size is
V = 10,000and the embedding size isN = 300. - The embedding matrix
Ewill have shape(V, N).
To retrieve the embedding of word i, simply use:
embedding_vector = E[i]
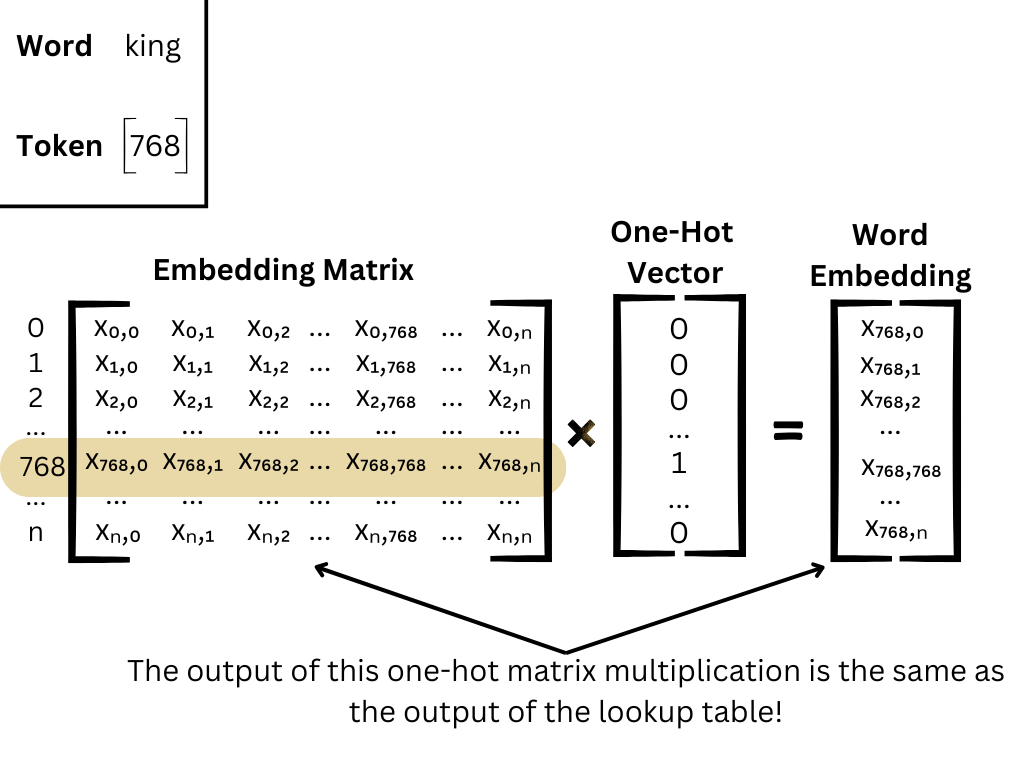
This matrix is updated during training so that embeddings capture task-specific information.
Learning Word Embeddings
Word embeddings can be learned in two ways:
- Supervised Learning: Train a model on a downstream task (e.g., sentiment classification) and update embeddings during training.
- Unsupervised Learning: Train embeddings on large text corpora to learn general-purpose representations (e.g., Word2Vec, GloVe).
Word2Vec
Word2Vec is a popular unsupervised model for learning word embeddings. It has two architectures:
Architectures: CBOW vs Skip-Gram
Word2Vec comes in two main model architectures:
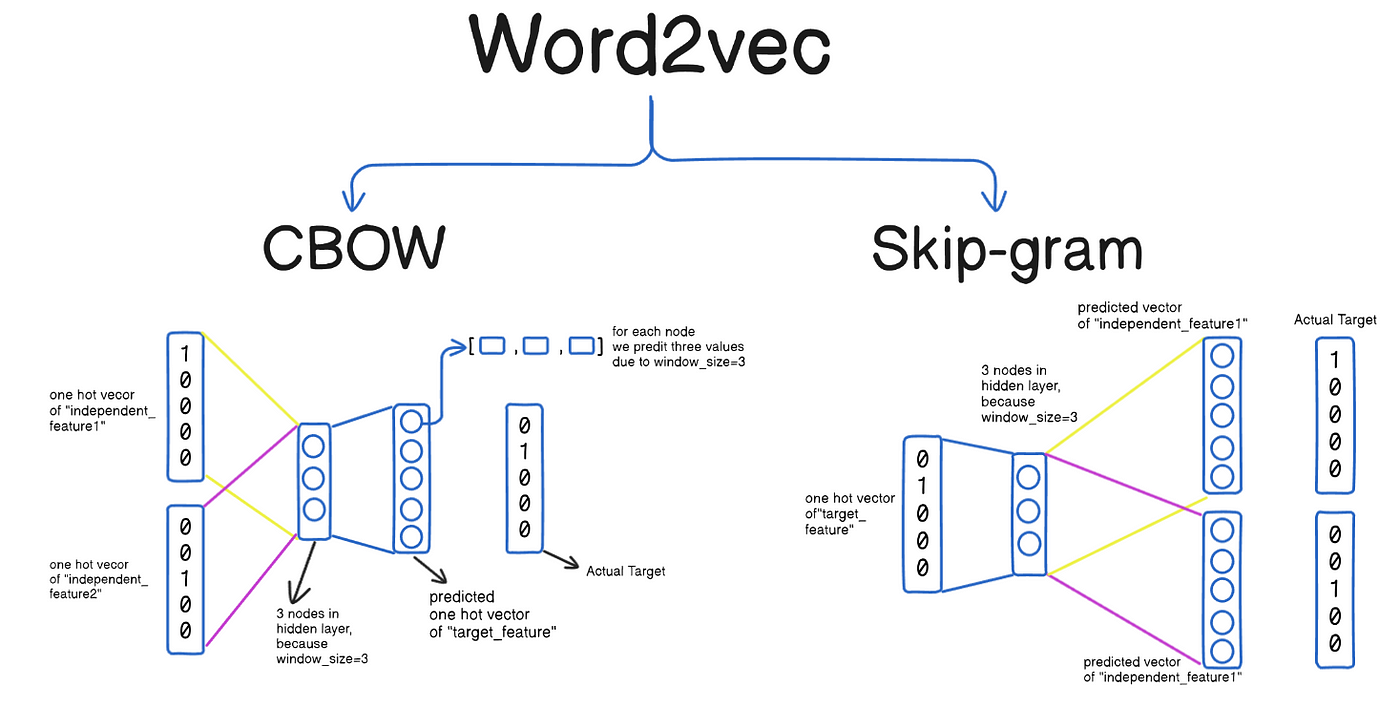
-
Continuous Bag of Words (CBOW):
Predicts the current word based on its context.
Given the surrounding words, the model tries to guess the center word.
Efficient for larger datasets and more frequent words.Example:
- Input: ["the", "cat", "on", "the", "mat"]
- Center Word: "sat"
- Context: ["the", "cat", "on", "the", "mat"]
- CBOW tries to predict "sat" from the context.
-
Skip-Gram:
Predicts surrounding context words given the current word.
Given the center word, the model tries to predict the context.
Performs well with smaller datasets and rare words.Example:
- Input: "sat"
- Target Outputs: ["the", "cat", "on", "the", "mat"]
- Skip-Gram tries to predict the surrounding words from "sat".
How Word2Vec Learns Word Embeddings
- Word2Vec uses a shallow neural network with one hidden layer.
- The vocabulary size is
V, and the desired vector size isN. - The input layer is a one-hot vector of size
V. - The hidden layer (no activation function) has size
N. - The output layer is also of size
V, predicting a probability distribution over all words.
Steps:
- Convert the input word into a one-hot encoded vector.
- Multiply it by the input weight matrix to get the hidden layer representation.
- Multiply that by the output weight matrix to get scores for all words in the vocabulary.
- Apply softmax to produce a probability distribution.
- Update weights via backpropagation using gradient descent to minimize the loss.
Training Objective: Maximizing Log Probability
For the Skip-Gram model, the goal is to maximize the average log probability:
Where:
- is the total number of words in the corpus.
- is the context window size.
- is the center word, and are the context words.
Computational Challenge: Softmax and Large Vocabulary
Calculating the softmax over a large vocabulary is computationally expensive. To address this, Word2Vec introduces optimization techniques such as:
- Negative Sampling
- Hierarchical Softmax
These methods significantly reduce the training time while maintaining the quality of the learned embeddings.
Example: Learning from a Sentence
Suppose the sentence is:
"The quick brown fox jumps over the lazy dog"
With a context window of size 2, for the center word "brown", the context is ["The", "quick", "fox", "jumps"].
In the Skip-Gram model, we would train the network to predict each of those context words from "brown".
Why Word2Vec Works
Word2Vec learns useful representations because:
- It captures both syntactic and semantic relationships.
- It leverages co-occurrence statistics of words in a corpus.
- The vector space preserves many linguistic regularities.
For instance:
vec("Paris") - vec("France") + vec("Italy") ≈ vec("Rome")vec("walking") - vec("walk") + vec("swim") ≈ vec("swimming")
Applications of Word2Vec
- Text classification
- Sentiment analysis
- Named entity recognition
- Question answering
- Semantic search
- Machine translation
These embeddings can be pre-trained (e.g., on Google News) or trained on custom corpora to tailor them to specific domains (e.g., medical texts, legal documents).
Negative Sampling
In Word2Vec, instead of updating weights for all words in the vocabulary, negative sampling updates only a few:
- Pick one positive pair (word and context).
- Sample
knegative words randomly.
This improves efficiency dramatically and allows the model to scale to large corpora.
Loss function (simplified):
Where:
v_wis the input word vectorv_cis the context vectorP_n(w)is the noise distribution
GloVe Word Vectors
GloVe (Global Vectors for Word Representation) is an alternative to Word2Vec. It constructs a co-occurrence matrix X and models the relationships between words based on their global co-occurrence statistics.
Cost function:
Where:
- = number of times word co-occurs with word
- , = word vectors
- , = biases
- = weighting function
This approach captures both local and global word relationships.
Sentiment Classification
Word embeddings can be used as inputs to models like LSTM or CNN for tasks such as sentiment analysis.
Example workflow:
- Convert text to sequence of embeddings.
- Feed sequence into an LSTM.
- Predict a sentiment label: positive, negative, or neutral.
Embeddings help capture contextual sentiment information that traditional methods might miss.
Debiasing Word Embeddings
Word embeddings can reflect and amplify societal biases (e.g., gender bias).
Example:
- vector("doctor") might be closer to vector("man") than vector("woman") in biased embeddings.
Debiasing Techniques:
- Identify bias subspace: e.g., direction of gender (he-she).
- Neutralize: Make gender-neutral words (e.g., "doctor") orthogonal to the gender direction.
- Equalize: Adjust word pairs (e.g., "man" and "woman") to be equidistant from neutral terms.
These techniques are essential to make NLP applications fair and inclusive.
This concludes a comprehensive overview of word embeddings and their usage in natural language processing. Each concept here forms the foundation for more advanced NLP models such as Transformers and BERT.