Overfitting and Regularization

• 1. The Problem of Overfitting
  • What is Overfitting?
  • Symptoms of Overfitting
  • Example of Overfitting in Regression
    • Overfitting vs. Underfitting
    • Visualization of Overfitting
• 2. Addressing Overfitting
  • 1. Collecting More Data
  • 2. Feature Selection & Engineering
  • 3. Cross-Validation
  • 4. Regularization as a Solution
• 3. Regularized Cost Function
  • 1. Why Modify the Cost Function?
  • 2. Adding Regularization Term
    • L2 Regularization (Ridge Regression)
    • L1 Regularization (Lasso Regression)
  • 3. Effect of Regularization on Model Complexity
    • Visualization of Regularization Effects
• 4. Regularized Linear Regression
  • 1. Linear Regression Cost Function (Without Regularization)
  • 2. Regularized Cost Function for Linear Regression
  • 3. Effect of Regularization in Gradient Descent
    • Effect of Regularization on Parameters
  • 4. Normal Equation with Regularization
  • 5. Summary
• 5. Regularized Logistic Regression
  • 1. Logistic Regression Cost Function (Without Regularization)
  • 2. Regularized Cost Function for Logistic Regression
  • 3. Effect of Regularization in Gradient Descent
  • 4. Decision Boundary and Regularization
  • 5. Summary

1. The Problem of Overfitting

What is Overfitting?

Overfitting occurs when a machine learning model learns the training data too well, capturing noise and random fluctuations rather than the underlying pattern. As a result, the model performs well on training data but generalizes poorly to unseen data.

Symptoms of Overfitting

• High training accuracy but low test accuracy (poor generalization).
• Complex decision boundaries that fit training data too closely.
• Large model parameters (high magnitude weights), leading to excessive sensitivity to small changes in input data.

Example of Overfitting in Regression

Consider a polynomial regression model. If we fit a high-degree polynomial to data, the model may pass through all training points perfectly but fail to predict new data correctly.

Overfitting vs. Underfitting

Visualization of Overfitting

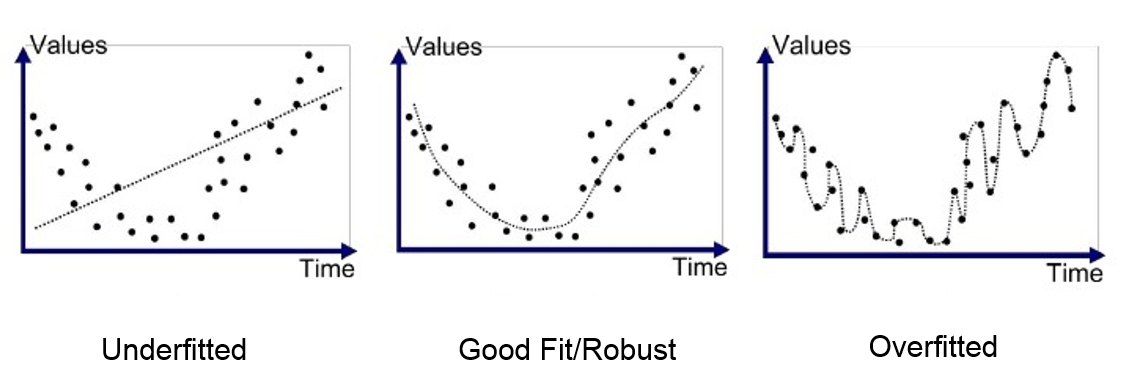
• Left (Underfitting): The model is too simple and cannot capture the trend.
• Middle (Good Fit): The model captures the pattern without overcomplicating.
• Right (Overfitting): The model follows the training data too closely, failing on new inputs.

2. Addressing Overfitting

Overfitting occurs when a model learns noise instead of the underlying pattern in the data. To address overfitting, we can apply several strategies to improve the model’s ability to generalize to unseen data.

1. Collecting More Data

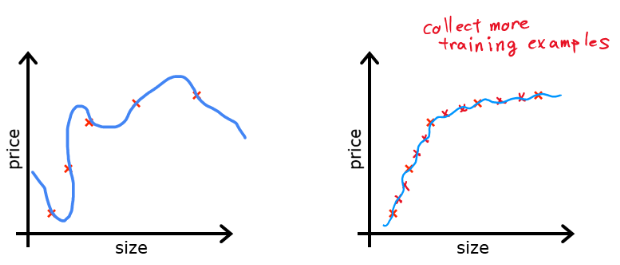
• More training data helps the model capture real patterns rather than memorizing noise.
• Especially effective for deep learning models, where small datasets tend to overfit quickly.
• Not always feasible, but can be supplemented with data augmentation techniques.

2. Feature Selection & Engineering

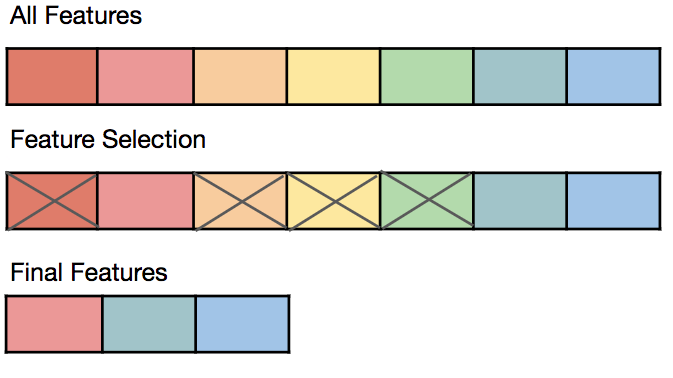
• Removing irrelevant or redundant features reduces model complexity.
• Techniques like Principal Component Analysis (PCA) help reduce dimensionality.
• Engineering new features (e.g., creating polynomial features or interaction terms) can improve generalization.

3. Cross-Validation

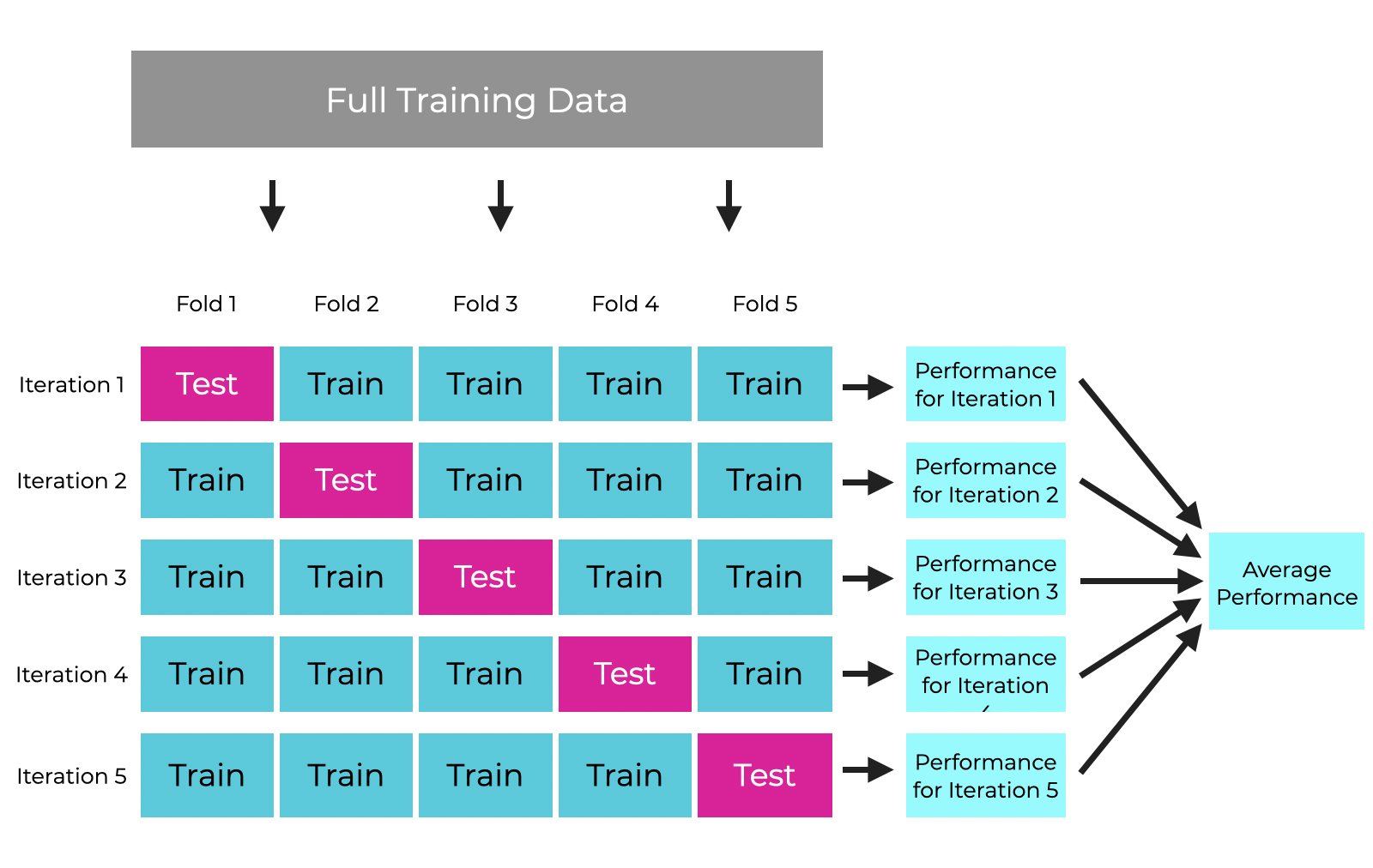
• k-fold cross-validation ensures that the model performs well on different data splits.
• Helps detect overfitting early by testing the model on multiple subsets of data.
• Leave-one-out cross-validation (LOOCV) is another approach, especially useful for small datasets.

4. Regularization as a Solution

• Regularization techniques add constraints to the model to prevent excessive complexity.
• L1 (Lasso) and L2 (Ridge) Regularization introduce penalties for large coefficients.
• We will explore regularized cost functions in the next section.

By applying these techniques, we control model complexity and improve generalization performance. In the next section, we will dive deeper into regularization and its role in the cost function.

3. Regularized Cost Function

Overfitting often occurs when a model learns excessive complexity, leading to poor generalization. One way to control this is by modifying the cost function to penalize overly complex models.

1. Why Modify the Cost Function?

The standard cost function in regression or classification only minimizes the error on training data, which can result in large coefficients (weights) that overfit the data.

By adding a regularization term, we discourage large weights, making the model simpler and reducing overfitting.

2. Adding Regularization Term

Regularization adds a penalty term to the cost function that shrinks the model parameters. The two most common types of regularization are:

L2 Regularization (Ridge Regression)

In L2 regularization, we add the sum of squared weights to the cost function:

$$J(\theta )=\frac{1}{m}\sum _{i=1}^m{\left[h_{\theta }(x^{(i)})-y^{(i)}\right]}^2+\lambda \sum _{j=1}^n{\theta }_j^2$$

• $\lambda$ (regularization parameter) controls how much regularization is applied.
• Higher $\lambda$ values force the model to reduce the magnitude of parameters, preventing overfitting.
• L2 regularization keeps all features but reduces their impact.

L1 Regularization (Lasso Regression)

In L1 regularization, we add the absolute values of weights:

$$J(\theta )=\frac{1}{m}\sum _{i=1}^m{\left[h_{\theta }(x^{(i)})-y^{(i)}\right]}^2+\lambda \sum _{j=1}^n|{\theta }_j|$$

• L1 regularization pushes some coefficients to zero, effectively performing feature selection.
• It results in sparser models, which are useful when many features are irrelevant.

3. Effect of Regularization on Model Complexity

Regularization controls model complexity by restricting parameter values:

• No Regularization ($\lambda =0$) → The model fits the training data too closely (overfitting).
• Small $\lambda$ → The model is still flexible but generalizes better.
• Large $\lambda$ → The model becomes too simple (underfitting), losing important patterns.

Visualization of Regularization Effects

• Left (No Regularization): The model overfits training data.
• Middle (Moderate Regularization): The model generalizes well.
• Right (Strong Regularization): The model underfits the data.

4. Regularized Linear Regression

Linear regression without regularization can suffer from overfitting, especially when the model has too many features or when training data is limited. Regularization helps by constraining the model's parameters, preventing extreme values that lead to high variance.

1. Linear Regression Cost Function (Without Regularization)

The standard cost function for linear regression is:

$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }(x^{(i)})-y^{(i)}\right)}^2$$

where:

• $h\_\theta (x)={\theta }^{T}x$ is the hypothesis (predicted value),
• $m$ is the number of training examples.

This function minimizes the sum of squared errors but does not impose any restrictions on the parameter values, which can lead to overfitting.

2. Regularized Cost Function for Linear Regression

To prevent overfitting, we add an L2 regularization term (also known as Ridge Regression) to penalize large parameter values:

$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }(x^{(i)})-y^{(i)}\right)}^2+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$

where:

• $\lambda$ is the regularization parameter that controls the penalty,
• The term $\sum {\theta }_j^2$ penalizes large values of $\theta$,
• ${\theta }_0$ (bias term) is not regularized.

3. Effect of Regularization in Gradient Descent

Regularization modifies the gradient descent update rule:

$${\theta }_j:={\theta }_j-\alpha \left[\frac{1}{m}\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)x_j+\frac{\lambda }{m}{\theta }_j\right]$$

• The additional term $\frac{\lambda }{m}{\theta }_j$ shrinks the parameter values over time.
• When $\lambda$ is too large, the model underfits (too simple).
• When $\lambda$ is too small, the model overfits (too complex).

Effect of Regularization on Parameters

• If $\lambda =0$: Regularization is off → Overfitting risk.
• If $\lambda$ is too high: Model is too simple → Underfitting.
• If $\lambda$ is optimal: Good generalization → Balanced model.

4. Normal Equation with Regularization

For linear regression, we can solve for $\theta$ using the Normal Equation, which avoids gradient descent:

$$\theta =(X^{T}X+\lambda I{)}^{-1}{X}^{T}y$$

where:

• $I$ is the identity matrix (except ${\theta }_0$ is not regularized).
• Adding $\lambda I$ ensures $X^{T}X$ is invertible, reducing multicollinearity issues.

5. Summary

✅ Regularization reduces overfitting by penalizing large weights.
✅ L2 regularization (Ridge Regression) modifies cost function by adding $\sum {\theta }_j^2$.
✅ Gradient Descent and Normal Equation both adjust to include regularization.
✅ Choosing $\lambda$ is critical: too high → underfitting, too low → overfitting.

5. Regularized Logistic Regression

Logistic regression is commonly used for classification tasks, but like linear regression, it can overfit when there are too many features or limited data. Regularization helps control overfitting by penalizing large parameter values.

1. Logistic Regression Cost Function (Without Regularization)

The standard cost function for logistic regression is:

$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m\left[y^{(i)}\log h_{\theta }(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))\right]$$

where:

• $h\_\theta (x)=\frac{1}{1+e^{-{\theta }^{T}x}}$ is the sigmoid function,
• $y$ is the actual class label ($0$ or $1$),
• $m$ is the number of training examples.

This cost function does not include regularization, meaning the model may assign large weights to some features, leading to overfitting.

2. Regularized Cost Function for Logistic Regression

To reduce overfitting, we add an L2 regularization term, similar to regularized linear regression:

$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m\left[y^{(i)}\log h_{\theta }(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))\right]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$

where:

• $\lambda$ is the regularization parameter (controls penalty),
• The term $\sum {\theta }_j^2$ discourages large parameter values,
• ${\theta }_0$ (bias term) is NOT regularized.

✅ Effect of Regularization

• Small $\lambda$ → Model may overfit (complex decision boundary).
• Large $\lambda$ → Model may underfit (too simple, missing important features).
• Optimal $\lambda$ → Model generalizes well.

3. Effect of Regularization in Gradient Descent

Regularization modifies the gradient descent update rule:

$${\theta }_j:={\theta }_j-\alpha \left[\frac{1}{m}\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)x_j+\frac{\lambda }{m}{\theta }_j\right]$$

• The regularization term $\frac{\lambda }{m}{\theta }_j$ shrinks the weight values over time.
• Helps avoid models that memorize training data instead of learning patterns.

4. Decision Boundary and Regularization

Regularization also affects decision boundaries:

• Without regularization ($\lambda =0$): Complex boundaries that fit noise.
• With moderate $\lambda$: Simpler boundaries that generalize better.
• With very high $\lambda$: Too simplistic boundaries that underfit.

5. Summary

✅ Regularization in logistic regression prevents overfitting by controlling parameter sizes.
✅ L2 regularization (Ridge Regression) adds $\sum {\theta }_j^2$ to cost function.
✅ Gradient Descent is adjusted to shrink large weights.
✅ Choosing $\lambda$ is critical for a well-generalized model.