Neural Networks: Intuition and Model

• Understanding Neural Networks
• Biological Inspiration: The Brain and Synapses
  • Structure of a Biological Neuron
  • Artificial Neural Networks vs. Biological Networks
• Importance of Layers in Neural Networks
  • Example: Predicting a T-shirt's Top-Seller Status
• Face Recognition Example: Layer-by-Layer Processing
• Mathematical Representation of a Neural Network
  • Example Calculation
  • Two Hidden Layer Neural Network Calculation
    • Network Structure
    • First Hidden Layer Calculation
    • Second Hidden Layer Calculation
    • Output Layer Calculation
  • Conclusion
  • Handwritten Digit Recognition Using Two Layers
    • First Layer: Feature Extraction
    • Second Layer: Pattern Recognition
    • Output Layer: Classification

Understanding Neural Networks

Neural networks are a fundamental concept in deep learning, inspired by the way the human brain processes information. They consist of layers of artificial neurons that transform input data into meaningful outputs. At the core of a neural network is a simple mathematical operation: each neuron receives inputs, applies a weighted sum, adds a bias term, and passes the result through an activation function. This process allows the network to learn patterns and make predictions.

Biological Inspiration: The Brain and Synapses

Artificial neural networks (ANNs) are designed based on the biological structure of the human brain. The brain consists of billions of neurons, interconnected through structures called synapses. Neurons communicate with each other by transmitting electrical and chemical signals, which play a critical role in learning, memory, and decision-making processes.

Structure of a Biological Neuron

Each biological neuron consists of several key components:

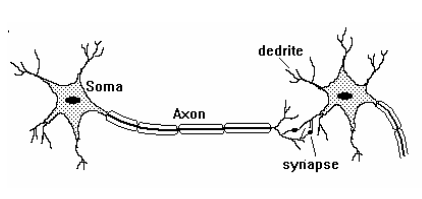
• Dendrites: Receive input signals from other neurons.
• Cell Body (Soma): Processes the received signals and determines whether the neuron should be activated.
• Axon: Transmits the output signal to other neurons.
• Synapses: Junctions between neurons where chemical neurotransmitters facilitate communication.

Artificial Neural Networks vs. Biological Networks

In artificial neural networks:

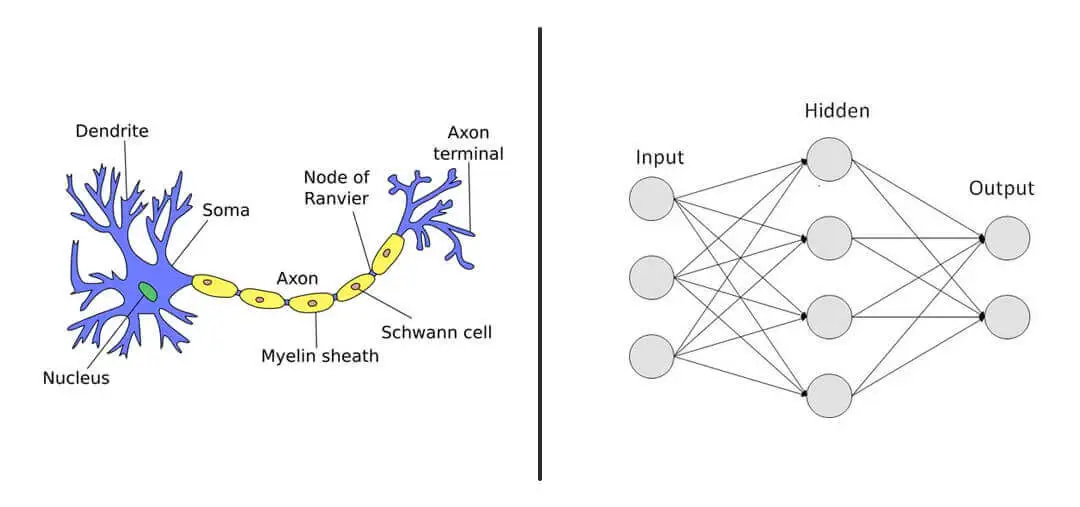
• Neurons function as computational units.
• Weights correspond to synaptic strengths, determining how influential an input is.
• Bias terms help shift the activation threshold.
• Activation functions mimic the way biological neurons fire only when certain thresholds are exceeded.

Importance of Layers in Neural Networks

Neural networks are composed of multiple layers, each responsible for extracting and processing features from input data. The more layers a network has, the deeper it becomes, allowing it to learn complex hierarchical patterns.

Example: Predicting a T-shirt's Top-Seller Status

Consider an online clothing store that wants to predict whether a new T-shirt will become a top-seller. Several factors influence this outcome, which serve as inputs to our neural network:

• Price ($x_1$)
• Shipping Cost ($x_2$)
• Marketing ($x_3$)
• Material ($x_4$)

These inputs are fed into the first layer of the network, which extracts meaningful features. A possible hidden layer structure could be:

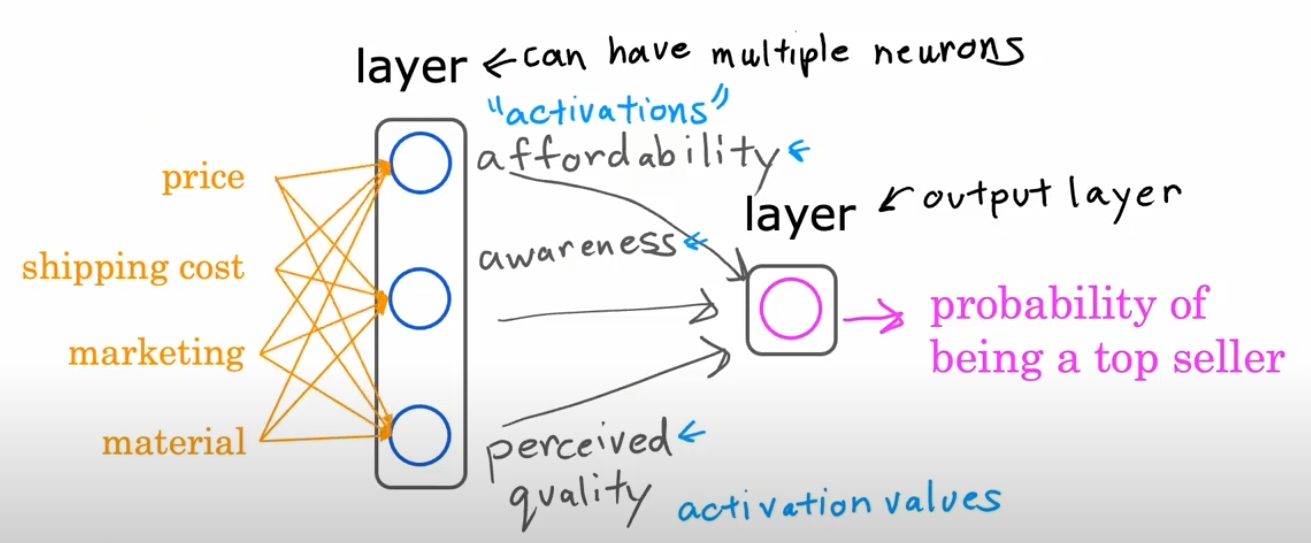
1. Hidden Layer 1: Contains a few activations functions like: affordability , awareness, perceived quality.
2. Output Layer: Aggregates information from the previous layers to make a final prediction.

The output layer applies a sigmoid activation function:

$$\sigma (z)=\frac{1}{1+e^{-z}}$$

where $z$ is a weighted sum of the previous layer’s outputs. If $\sigma (z)>0.5$, we classify the T-shirt as a top-seller; otherwise, it is not.

Face Recognition Example: Layer-by-Layer Processing

Face recognition is a real-world example where neural networks excel. Let's consider a deep neural network designed for face recognition, breaking down the processing step by step:

1. Input Layer: An image of a face is converted into pixel values (e.g., a 100x100 grayscale image would be represented as a vector of 10,000 pixel values).

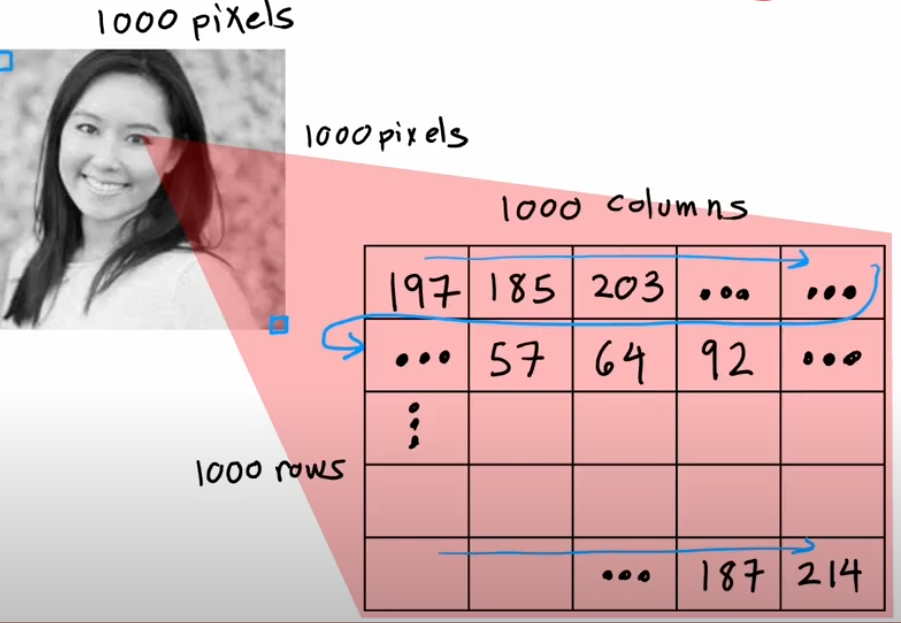
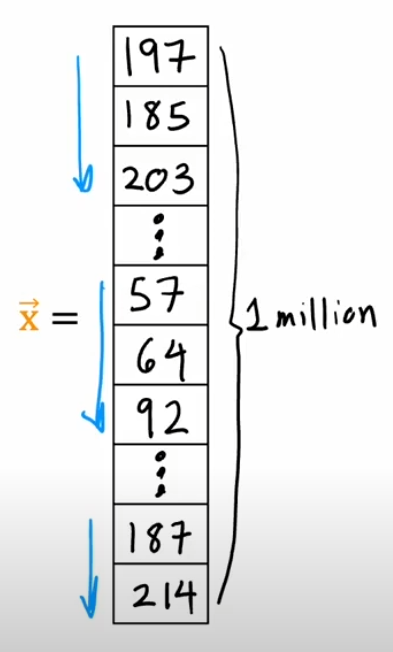
2. First Hidden Layer: Detects basic edges and corners in the image by applying simple filters.
3. Second Hidden Layer: Identifies facial features like eyes, noses, and mouths by combining edge and corner information.
4. Third Hidden Layer: Recognizes entire facial structures and relationships between features.

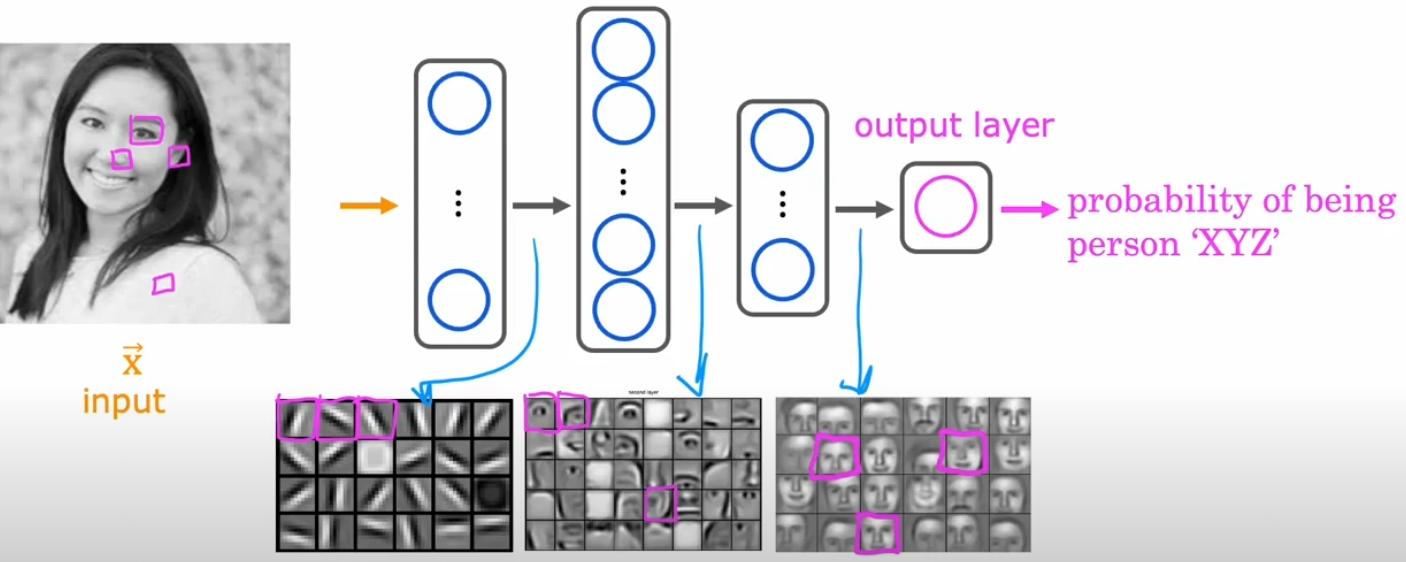
5. Output Layer: Determines whether the face matches a known identity by producing a probability score.

Mathematical Representation of a Neural Network

To efficiently compute activations in a neural network, we use matrix notation. The general formula for forward propagation is:

$$Z^{[l]}=W^{[l]}{A}^{[l-1]}+b^{[l]}$$

where:

• $A^{[l-1]}$ is the activation from the previous layer,
• $W^{[l]}$ is the weight matrix of the current layer,
• $b^{[l]}$ is the bias vector,
• $Z^{[l]}$ is the linear combination of inputs before applying the activation function.

The activation function is applied as:

$$A^{[l]}=g(Z^{[l]})$$

where $g$ is typically a sigmoid, ReLU, or softmax function.

Example Calculation

Suppose we have a single-layer neural network with three inputs and one neuron. We define the inputs as:

$$x_1=0.5,x_2=0.8,x_3=0.2$$

The corresponding weight matrix and bias term are given by:

$$W=\left[\begin{array}{ccc}0.9& -0.5& 0.3\end{array}\right],b=0.1$$

The weighted sum (Z) is calculated as:

$$Z=W\cdot X+b=(0.5\times 0.9)+(0.8\times -0.5)+(0.2\times 0.3)+0.1$$

$$Z=0.45-0.4+0.06+0.1=0.21$$

Applying the sigmoid activation function:

$$\sigma (Z)=\frac{1}{1+e^{-Z}}=\frac{1}{1+e^{-0.21}}\approx 0.552$$

Since the output is above 0.5, we classify this case as positive.

Two Hidden Layer Neural Network Calculation

Now, let's consider a neural network with two hidden layers.

Network Structure

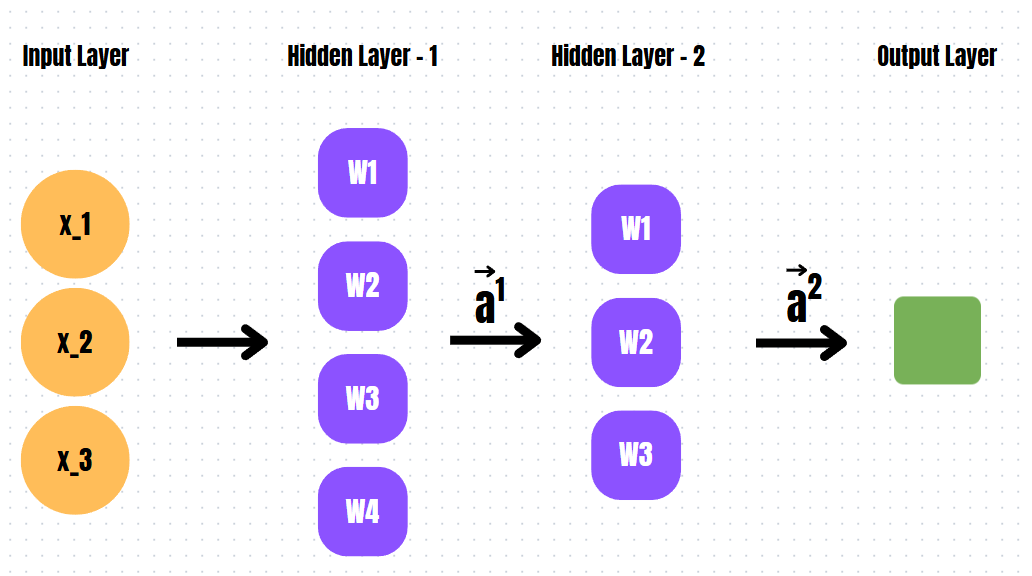
• Input Layer: 3 input values $X=[x_1,x_2,x_3]$
• First Hidden Layer: 4 neurons
• Second Hidden Layer: 3 neurons
• Output Layer: 1 neuron

First Hidden Layer Calculation

Given input vector:

$$X=\left[\begin{array}{c}0.5\\ 0.8\\ 0.2\end{array}\right]$$

Weight matrix for the first hidden layer:

$$W^{(1)}=\left[\begin{array}{ccc}0.2& -0.3& 0.5\\ -0.7& 0.1& 0.4\\ 0.3& 0.8& -0.6\\ 0.5& -0.2& 0.7\end{array}\right]$$

Bias vector:

$$b^{(1)}=\left[\begin{array}{c}0.1\\ -0.2\\ 0.3\\ 0.4\end{array}\right]$$

Computing the weighted sum:

$$Z^{(1)}=W^{(1)}X+b^{(1)}$$

Applying the sigmoid activation function:

$$A^{(1)}=\sigma (Z^{(1)})$$

Second Hidden Layer Calculation

Weight matrix:

$$W^{(2)}=\left[\begin{array}{cccc}0.6& -0.1& 0.3& 0.7\\ 0.2& 0.9& -0.5& 0.4\\ -0.3& 0.5& 0.7& -0.6\end{array}\right]$$

Bias vector:

$$b^{(2)}=\left[\begin{array}{c}-0.1\\ 0.3\\ 0.2\end{array}\right]$$

Computing the weighted sum:

$$Z^{(2)}=W^{(2)}{A}^{(1)}+b^{(2)}$$

Applying the sigmoid activation function:

$$A^{(2)}=\sigma (Z^{(2)})$$

Output Layer Calculation

Weight matrix:

$$W^{(3)}=\left[\begin{array}{ccc}0.5& -0.7& 0.6\end{array}\right]$$

Bias:

$$b^{(3)}=-0.2$$

Computing the final weighted sum:

$$Z^{(3)}=W^{(3)}{A}^{(2)}+b^{(3)}$$

Applying the sigmoid activation function:

$$A^{(3)}=\sigma (Z^{(3)})$$

If $A^{(3)}>0.5$, the output is classified as positive.

Conclusion

1. The first hidden layer extracts basic features.
2. The second hidden layer learns more abstract representations.
3. The output layer makes the final classification decision.

This demonstrates how a multi-layer neural network processes information in a hierarchical manner.

Handwritten Digit Recognition Using Two Layers

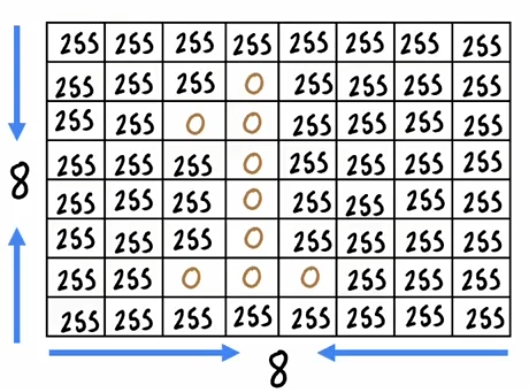
A classic application of neural networks is handwritten digit recognition. Let's consider recognizing the digit '1' from an 8x8 pixel grid using a simple neural network with two layers.

First Layer: Feature Extraction

• The 8x8 image is flattened into a 64-dimensional input vector.
• This vector is processed by neurons in the first hidden layer.
• The neurons identify edges, curves, and simple shapes using learned weights.
• Mathematically, the output of the first layer can be represented as:

$$Z^{(1)}=W^{(1)}X+b^{(1)}$$ $$A^{(1)}=\sigma (Z^{(1)})$$

Second Layer: Pattern Recognition

• The first layer's output is passed to a second hidden layer.
• This layer detects digit-specific features, such as the vertical stroke characteristic of '1'.
• The transformation at this stage follows:

$$Z^{(2)}=W^{(2)}{A}^{(1)}+b^{(2)}$$ $$A^{(2)}=\sigma (Z^{(2)})$$

Output Layer: Classification

• The final layer has 10 neurons, each representing a digit from 0 to 9.
• The neuron with the highest activation determines the predicted digit:

$$Z^{(3)}=W^{(3)}{A}^{(2)}+b^{(3)}$$ $$\text{Prediction}=\arg \max (A^{(3)})$$

This structured approach demonstrates how neural networks model real-world problems, from binary classification to deep learning applications like face and handwriting recognition.